CMS-Flow:Hiding and Exposure

Hiding and Exposure

When the bed material is composed of multiple grain sizes, larger grains have a greater probability of being exposed to the flow while smaller parti-cles have a greater probability of being hidden from the flow. 1 shows an example of a sediment grain (d_k) being hidden by d_k.

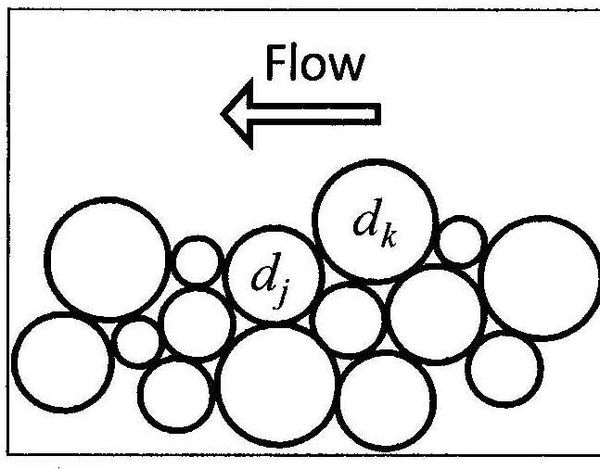
Figure 1. Schematic of the exposure height of bed sediment grains.

For the transport formulas described above, the hiding and exposure mechanism is considered by correcting the critical shear stress or velocity using a hiding and exposure correction function ($\zeta _{k}$). For the Lund-CIRP transport formula, an alternate approach is required due to the way in which the Shields number and grain size are included in the formulation; thus, the hiding and exposure correction function is directly used to multiply the transport rate. Two methods are used to calculate $\zeta _{k}$ depen-ding on whether the sediment transport model is run with a single sediment size or with multiple sediment sizes; the methods are described in the following sections.

Single-Sized Sediment Transport

At many sites, the bed material can be characterized by a single sediment size, with other sizes or materials (shell hash) which do not contribute significantly to morphology change, but do modify the sediment transport through hiding and exposure. By assuming that the spatial distribution of the bed material composition is constant in time, a hiding and exposure correction function can be introduced to correct the critical shields parameter $\theta _{ck}^{he}=\xi _{k}\theta _{ck}$ where $\xi _{k}$ is the dimensionless hiding and exposure function and $\theta _{ck}$ is the critical shear stress of the transport grain size. In CMS, a formula similar to that of Parker et al. (1995) and others is implemented $\xi _{k}=(d_{k}/d_{50})^{-m}$ where is the grain size corresponding to the 50th percentile, and $m$ is an empirical coefficient between 0.5-1.0 (default is 0.7).

The transport grain size is specified in the Advanced Card TRANSPORT_GRAIN_SIZE. The transport grain size should be the dominant grain size in the area of interest. To change the value of $m$ another Advanced Card HIDING_EXPOSURE_COEFFICIENT. If it is desired to test the model with a constant grain size and ignore the information in the D50_DATASET, the Advanced Card CONSTANT_GRAIN_SIZE.

Multiple-Sized Sediment Transport

For nonuniform sediments, the hiding and exposure is considered using a slightly modified form of the method proposed by Wu et al. (2000) which accounts information on the whole grain size distribution.

$\xi _{k}=(p_{ek}/p_{hk})^{-m}$

(2)

where $p_{ek}$ and $p_{hk}$ are the exposure and hiding probabilities calculated as

$p_{ek}=\sum _{j=1}^{N}p_{bj}{\frac {d_{j}}{d_{k}+d_{j}}},p_{hk}=\sum _{j=1}^{N}p_{bj}{\frac {d_{k}}{d_{k}+d_{j}}}$

(3)

References

---

Documentation Portal