CMS-Flow:Tech Report 3: Difference between revisions
Created page with "__notitle__ __NOTOC__ =Coastal Modeling System= left|thumb|400px|alt=Rudee Inlet '''Introduction''' The Coastal Modeling System (CMS) is an integra..." |
mNo edit summary |
||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
{{DISPLAYTITLE:Coastal Modeling System Technical Report 3}} | |||
[[File: | [[File:CMS_Framework.png|left|thumb|400px|alt=framework]] | ||
'''Introduction''' | '''Introduction''' | ||
The Coastal Modeling System (CMS) is an integrated numerical modeling | The Coastal Modeling System (CMS) is an integrated numerical modeling | ||
| Line 17: | Line 16: | ||
presented in Figure 1. | presented in Figure 1. | ||
<br style=clear:both /> | <br style=clear:both /> | ||
The CMS includes a flow model which calculates hydrodynamics and | |||
sediment transport and a wave model, all coupled together within the | |||
Surface-water Modeling System (SMS). The focus of this report, | |||
CMS-Flow, is a two-dimensional (2-D) depth-averaged nearshore | |||
circulation model. CMS-Flow calculates currents and water levels | |||
including physical processes such as advection, turbulent mixing, | |||
combined wave-current bottom friction; wind, wave, river, and tidal | |||
forcing forcing; Coriolis force; and the influence of coastal | |||
structures (Buttolph et al. 2006a; Wu et al. 2011). The implicit | |||
solver uses the SIMPLEC algorithm on a non-staggered grid to handle | |||
the coupling of water level and velocity. Primary variables u-, | |||
v-velocity, and water level are stored on the same set of grid points, | |||
and fluxes at cell faces are determined using a Rhie and Chow (1983) | |||
type momentum interpolation method (Wu et al. 2011). The explicit | |||
solver uses a staggered grid with velocities at the cell faces and the | |||
water levels and water depths at the cell centers (Buttolph | |||
et al. 2006a). CMS-Flow also calculates salinity and sediment | |||
transport and morphology change as discussed in a companion report | |||
(Sánchez and Wu 2011). CMS-Wave is a spectral wave transformation | |||
model and solves the wave-action balance equation using a forward | |||
marching Finite Difference Method (Mase et al.2005; Lin | |||
et al. 2008). CMS-Wave includes physical processes such as wave | |||
shoaling, refraction, diffraction, reflection, wave-current | |||
interaction, wave breaking, wind wave generation, white capping of | |||
waves, and the influence of coastal structures. The CMS takes | |||
advantage of the SMS interface (Zundel 2006) versions 8.2 through 11.1 | |||
for grid generation, model setup, plotting and post-processing of | |||
modeling results. The SMS also provides a link between the CMS and the | |||
Lagragian Particle Tracking Model (PTM) (MacDonald et al. 2006). | |||
Typical applications of CMS-Flow include the analyses of navigation | |||
channel performance; wave, current, and wave-current interaction in | |||
channels and in the vicinity of navigation structures; and sediment | |||
management transport issues around coastal inlets and adjacent | |||
beaches. Some examples of CMS-Flow applications are: Batten and Kraus | |||
(2006), Buttolph et al. (2006b), Zarillo and Brehin (2007), Li | |||
et al. (2009), Li et al. (2011), Beck and Kraus (2010), Byrnes | |||
et al. (2010), Rosati et al. (2011), Reed and Lin (2011), Wang and | |||
Beck (2011), and Watts et al (2011). | |||
'''Purpose of Study''' | |||
When a numerical model is developed, it should be verified and | |||
validated before it is applied in engineering practice. Verification | |||
is the process of determining the accuracy with which the governing | |||
equations of a specific model are being solved. It checks the | |||
numerical implementation of the governing equations. Validation is the | |||
process of determining the degree to which a model is an accurate | |||
representation of real world physics and processes from the | |||
perspective of the intended uses of the model. Another important term | |||
in model application is calibration, which is the process of | |||
determining the unknown model parameters or variables that represent | |||
physical quantities. Almost all nearshore models for hydrodynamics, | |||
waves and sediment transport have calibration parameters, such as | |||
bottom friction and sediment transport scaling factors. Estimating | |||
appropriate values for these parameters based on the problem | |||
considered is still an active area of research. Many of the | |||
calibration parameters are due to simplification and parameterization | |||
of the physics. Even a well verified and validated model may still | |||
need to be calibrated for different practical problems. | |||
This report documents details of the Verification and Validation (V&V) | |||
CMS-Flow | study conducted by the Coastal Inlets Research Program (CIRP) to | ||
evaluate the modeling capabilities of the CMS. The V&V study is | |||
divided into four separate reports: (I) Executive Summary (Demirbilek | |||
and Rosati 2011), (II) CMS-Wave (Lin et al. 2011), (III) CMS-Flow: | |||
Hydrodynamics (present report), and (IV) CMS-Flow: Sediment transport | |||
and morphology change (Sánchez et al. 2011). These reports describe | |||
detailed aspects of the V&V evaluations, applications, and resulting | |||
model performance skills. In the present report, hydrodynamic | |||
implementation within the CMS-Flow model is verified and validated | |||
using idealized, laboratory, and field test cases. The model | |||
performance is evaluated using several goodness-of-fit statistics (see | |||
Appendix A). One objective of the V&V study is to determine | |||
appropriate ranges for hydrodynamic parameters for different | |||
applications and establish a basis for user guidance. Future | |||
improvements are identified to enhance CIRP model’s unique features | |||
and computational capabilities for practical applications. The report | |||
represents the first of a series of hydrodynamic V&V reports and is | |||
not intended to be comprehensive. Additional cases, and extended | |||
results and discussion of the test cases provided here are posted to | |||
the CMS wiki http://cirp.usace.army.mil/wiki/CMS. | |||
'''CMS Hydrodynamics''' | |||
CMS-Flow calculates depth-averaged hydrodynamics by solving the | |||
conservative form of the shallow water equations using the Finite | |||
Volume Method on a regular or telescoping Cartesian mesh. The regular | |||
Cartesian mesh only allows a cell to have a maximum of 4 neighbors and | |||
has a fixed number of columns and rows, but may have a spatially | |||
variable grid resolution. When the grid resolution varies along either | |||
of the coordinates, the grid is referred to as a nonuniform Cartesian | |||
grid. The telescoping Cartesian grid allows a computational cell to | |||
have up to six neighbors and up to two on the same direction | |||
(e.g. North, South, East, and West). Telescoping grids are supported | |||
in SMS versions 11.0 and above. Presently, the SMS interface can only | |||
generate telescoping grids with a spatially constant cell aspect ratio | |||
and only supports isotropic grid refinement (1 cell is split into 4 | |||
cells). These grids resemble quad-tree grids. However, the term | |||
quad-tree is avoided here because the data structure used is not a | |||
quad-tree and the numerical discretization is not limited to quad-tree | |||
grids. For both the regular and telescoping Cartesian grids, the | |||
inactive (permanently dry cells) portions of the grids are removed and | |||
variable information is stored in 1-D arrays with the cell | |||
connectivity specified by lookup tables in the same way as in an | |||
unstructured mesh. This approach reduces computational memory, allows | |||
for efficient vectorized computations, and provides a simple framework | |||
for anisoptric grid refinement (1 cell is split into 2 cells). | |||
In important aspect to any practical engineering hydrodynamic model is | |||
the boundary condition (BC) treatment and specification. CMS-Flow | |||
offers several types of BCs. For most coastal applications, the ocean | |||
boundary is assigned a water level time series from a measured station | |||
and applied along the whole boundary. This BC type is simply referred | |||
to as a Water Level BC. If water level measurements are not available, | |||
tidal constituents may be entered manually and applied on the whole | |||
ocean boundary (Tidal Constituent BC). It is noted that in the | |||
implicit flow solver, the water level is applied as a source (forcing) | |||
term, and is not strictly enforced (clamped) which provides better | |||
stability and performance. In the explicit flow solver, the water | |||
level is clamped. For cases in which the ocean domain is relatively | |||
large and spatially variable water levels or velocities occur, water | |||
level and velocity (flux) BCs are available. The spatially variable | |||
water levels and velocities may be extracted from a larger regional | |||
models such as ADCIRC (Luettich et al. 1992) or CMS simulation or from | |||
a tidal constituent database. When applying a Water Level BC to the | |||
nearshore, the wave-induced setup is not included and can lead to | |||
local flow reversals and boundary problems. In the explicit flow | |||
solver, this problem is avoided by implementing a Wave-adjusted Water | |||
Level BC (Reed and Militello 2005). In the implicit flow solver a | |||
similar wave-adjusted BC is applied by solving the 1-D cross-shore | |||
momentum equation including wave and wind forcing (Wu et al. 2011a, | |||
2011b). | |||
The hydrodynamics is coupled to sediment transport (also in CMS-Flow) | |||
and the wave model, CMS-Wave. Some important features and processes | |||
included are: wetting and drying, wave and surface roller stresses, | |||
wave mass fluxes, wave-enhanced bottom friction, turbulent diffusion, | |||
wall friction, Coriolis force, spatially variable wind and atmospheric | |||
pressure, and vegetation flow drag. Both explicit and implicit time | |||
marching schemes are available. The explicit scheme is designed for | |||
highly transient flow and extreme wetting and drying problems which | |||
require small time steps. The implicit scheme is designed for tidal | |||
flow and long-term simulations where large time steps can be used on | |||
the order of 10 min. CMS versions 4.0 and higher have both CMS-Wave | |||
and CMS-Flow in a single executable (code) for faster and more | |||
efficient model coupling. The CMS is parallelized using | |||
OpenMP. Additional information about CMS-Flow is available from the | |||
CIRP website: http://cirp.usace.army.mil/wiki/CMS-Flow. | |||
'''Study Plan''' | |||
Three Categories of data sources are used in this V&V study to | |||
evaluate performance of CMS-Flow: analytical/empirical solutions | |||
(Category 1), laboratory studies (Category 2), and field experiments | |||
(Category 3). Test examples chosen included some known analytical | |||
solutions and idealized problems, laboratory studies with data, and | |||
field studies with data. Many test cases not included in this V&V | |||
report are being researched and these will be documented in future | |||
companion reports. | |||
'''Report Organization''' | |||
This report is organized in five chapters. Chapter 1 presents the | |||
motivation, definitions, and an overview of the CMS-Flow V&V | |||
study. Chapter 2 discusses Verification of CMS-Flow with analytical | |||
solutions and idealized cases (Category 1). Chapters 3 and 4 present | |||
Validation of CMS-Flow with comparison of model calculations to | |||
laboratory (Category 2) and field (Category 3) data, respectively. In | |||
Chapters 2-4, test cases are identified by Category “C” and Example | |||
number “Ex” as C1-Ex1, etc. Chapter 5 summarizes the study and | |||
discusses future work. Appendix A provides a description of the | |||
goodness-of-fit statistics applied herein. | |||
[[CMS-Wave:TR3-Chap2|Chapter 2]] | |||
Latest revision as of 20:43, 25 August 2020
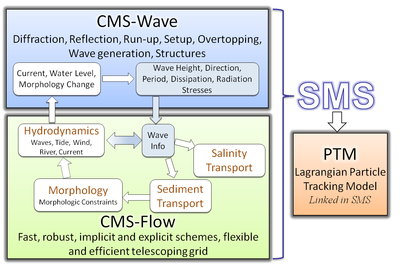
Introduction The Coastal Modeling System (CMS) is an integrated numerical modeling system for simulating nearshore waves, currents, water levels, sediment transport, and morphology change (Militello et al. 2004; Buttolph et al. 2006a; Lin et al. 2008; Reed et al. 2011). The system is designed for coastal inlets and navigation applications including channel performance and sediment exchange between inlets and adjacent beaches. Modeling provides planners and engineers essential information for improving the usage of USACE Operation and Maintenance Funds. CIRP is developing, testing, improving and transferring the CMS to Corps Districts and industry and assisting users in engineering studies. The overall framework of the CMS and its components are presented in Figure 1.
The CMS includes a flow model which calculates hydrodynamics and sediment transport and a wave model, all coupled together within the Surface-water Modeling System (SMS). The focus of this report, CMS-Flow, is a two-dimensional (2-D) depth-averaged nearshore circulation model. CMS-Flow calculates currents and water levels including physical processes such as advection, turbulent mixing, combined wave-current bottom friction; wind, wave, river, and tidal forcing forcing; Coriolis force; and the influence of coastal structures (Buttolph et al. 2006a; Wu et al. 2011). The implicit solver uses the SIMPLEC algorithm on a non-staggered grid to handle the coupling of water level and velocity. Primary variables u-, v-velocity, and water level are stored on the same set of grid points, and fluxes at cell faces are determined using a Rhie and Chow (1983) type momentum interpolation method (Wu et al. 2011). The explicit solver uses a staggered grid with velocities at the cell faces and the water levels and water depths at the cell centers (Buttolph et al. 2006a). CMS-Flow also calculates salinity and sediment transport and morphology change as discussed in a companion report (Sánchez and Wu 2011). CMS-Wave is a spectral wave transformation model and solves the wave-action balance equation using a forward marching Finite Difference Method (Mase et al.2005; Lin et al. 2008). CMS-Wave includes physical processes such as wave shoaling, refraction, diffraction, reflection, wave-current interaction, wave breaking, wind wave generation, white capping of waves, and the influence of coastal structures. The CMS takes advantage of the SMS interface (Zundel 2006) versions 8.2 through 11.1 for grid generation, model setup, plotting and post-processing of modeling results. The SMS also provides a link between the CMS and the Lagragian Particle Tracking Model (PTM) (MacDonald et al. 2006).
Typical applications of CMS-Flow include the analyses of navigation channel performance; wave, current, and wave-current interaction in channels and in the vicinity of navigation structures; and sediment management transport issues around coastal inlets and adjacent beaches. Some examples of CMS-Flow applications are: Batten and Kraus (2006), Buttolph et al. (2006b), Zarillo and Brehin (2007), Li et al. (2009), Li et al. (2011), Beck and Kraus (2010), Byrnes et al. (2010), Rosati et al. (2011), Reed and Lin (2011), Wang and Beck (2011), and Watts et al (2011).
Purpose of Study
When a numerical model is developed, it should be verified and validated before it is applied in engineering practice. Verification is the process of determining the accuracy with which the governing equations of a specific model are being solved. It checks the numerical implementation of the governing equations. Validation is the process of determining the degree to which a model is an accurate representation of real world physics and processes from the perspective of the intended uses of the model. Another important term in model application is calibration, which is the process of determining the unknown model parameters or variables that represent physical quantities. Almost all nearshore models for hydrodynamics, waves and sediment transport have calibration parameters, such as bottom friction and sediment transport scaling factors. Estimating appropriate values for these parameters based on the problem considered is still an active area of research. Many of the calibration parameters are due to simplification and parameterization of the physics. Even a well verified and validated model may still need to be calibrated for different practical problems.
This report documents details of the Verification and Validation (V&V) study conducted by the Coastal Inlets Research Program (CIRP) to evaluate the modeling capabilities of the CMS. The V&V study is divided into four separate reports: (I) Executive Summary (Demirbilek and Rosati 2011), (II) CMS-Wave (Lin et al. 2011), (III) CMS-Flow: Hydrodynamics (present report), and (IV) CMS-Flow: Sediment transport and morphology change (Sánchez et al. 2011). These reports describe detailed aspects of the V&V evaluations, applications, and resulting model performance skills. In the present report, hydrodynamic implementation within the CMS-Flow model is verified and validated using idealized, laboratory, and field test cases. The model performance is evaluated using several goodness-of-fit statistics (see Appendix A). One objective of the V&V study is to determine appropriate ranges for hydrodynamic parameters for different applications and establish a basis for user guidance. Future improvements are identified to enhance CIRP model’s unique features and computational capabilities for practical applications. The report represents the first of a series of hydrodynamic V&V reports and is not intended to be comprehensive. Additional cases, and extended results and discussion of the test cases provided here are posted to the CMS wiki http://cirp.usace.army.mil/wiki/CMS.
CMS Hydrodynamics
CMS-Flow calculates depth-averaged hydrodynamics by solving the conservative form of the shallow water equations using the Finite Volume Method on a regular or telescoping Cartesian mesh. The regular Cartesian mesh only allows a cell to have a maximum of 4 neighbors and has a fixed number of columns and rows, but may have a spatially variable grid resolution. When the grid resolution varies along either of the coordinates, the grid is referred to as a nonuniform Cartesian grid. The telescoping Cartesian grid allows a computational cell to have up to six neighbors and up to two on the same direction (e.g. North, South, East, and West). Telescoping grids are supported in SMS versions 11.0 and above. Presently, the SMS interface can only generate telescoping grids with a spatially constant cell aspect ratio and only supports isotropic grid refinement (1 cell is split into 4 cells). These grids resemble quad-tree grids. However, the term quad-tree is avoided here because the data structure used is not a quad-tree and the numerical discretization is not limited to quad-tree grids. For both the regular and telescoping Cartesian grids, the inactive (permanently dry cells) portions of the grids are removed and variable information is stored in 1-D arrays with the cell connectivity specified by lookup tables in the same way as in an unstructured mesh. This approach reduces computational memory, allows for efficient vectorized computations, and provides a simple framework for anisoptric grid refinement (1 cell is split into 2 cells).
In important aspect to any practical engineering hydrodynamic model is the boundary condition (BC) treatment and specification. CMS-Flow offers several types of BCs. For most coastal applications, the ocean boundary is assigned a water level time series from a measured station and applied along the whole boundary. This BC type is simply referred to as a Water Level BC. If water level measurements are not available, tidal constituents may be entered manually and applied on the whole ocean boundary (Tidal Constituent BC). It is noted that in the implicit flow solver, the water level is applied as a source (forcing) term, and is not strictly enforced (clamped) which provides better stability and performance. In the explicit flow solver, the water level is clamped. For cases in which the ocean domain is relatively large and spatially variable water levels or velocities occur, water level and velocity (flux) BCs are available. The spatially variable water levels and velocities may be extracted from a larger regional models such as ADCIRC (Luettich et al. 1992) or CMS simulation or from a tidal constituent database. When applying a Water Level BC to the nearshore, the wave-induced setup is not included and can lead to local flow reversals and boundary problems. In the explicit flow solver, this problem is avoided by implementing a Wave-adjusted Water Level BC (Reed and Militello 2005). In the implicit flow solver a similar wave-adjusted BC is applied by solving the 1-D cross-shore momentum equation including wave and wind forcing (Wu et al. 2011a, 2011b).
The hydrodynamics is coupled to sediment transport (also in CMS-Flow)
and the wave model, CMS-Wave. Some important features and processes
included are: wetting and drying, wave and surface roller stresses,
wave mass fluxes, wave-enhanced bottom friction, turbulent diffusion,
wall friction, Coriolis force, spatially variable wind and atmospheric
pressure, and vegetation flow drag. Both explicit and implicit time
marching schemes are available. The explicit scheme is designed for
highly transient flow and extreme wetting and drying problems which
require small time steps. The implicit scheme is designed for tidal
flow and long-term simulations where large time steps can be used on
the order of 10 min. CMS versions 4.0 and higher have both CMS-Wave
and CMS-Flow in a single executable (code) for faster and more
efficient model coupling. The CMS is parallelized using
OpenMP. Additional information about CMS-Flow is available from the
CIRP website: http://cirp.usace.army.mil/wiki/CMS-Flow.
Study Plan
Three Categories of data sources are used in this V&V study to evaluate performance of CMS-Flow: analytical/empirical solutions (Category 1), laboratory studies (Category 2), and field experiments (Category 3). Test examples chosen included some known analytical solutions and idealized problems, laboratory studies with data, and field studies with data. Many test cases not included in this V&V report are being researched and these will be documented in future companion reports.
Report Organization
This report is organized in five chapters. Chapter 1 presents the motivation, definitions, and an overview of the CMS-Flow V&V study. Chapter 2 discusses Verification of CMS-Flow with analytical solutions and idealized cases (Category 1). Chapters 3 and 4 present Validation of CMS-Flow with comparison of model calculations to laboratory (Category 2) and field (Category 3) data, respectively. In Chapters 2-4, test cases are identified by Category “C” and Example number “Ex” as C1-Ex1, etc. Chapter 5 summarizes the study and discusses future work. Appendix A provides a description of the goodness-of-fit statistics applied herein.