TAPtides: Difference between revisions

From CIRPwiki
Jump to navigation Jump to search
No edit summary
No edit summary
 
(47 intermediate revisions by the same user not shown)
Line 1: Line 1:
<font size = "6">'''Tidal Analysis and Prediction of Currents:  TAPcurrents</font>
__NOTOC__
<big>
 
<font size = "6">'''Tidal Analysis and Prediction of Tides:  TAPtides</font>


'''''By John D. Boon and Alejandro Sanchez'''''
'''''By John D. Boon and Alejandro Sanchez'''''
 
==Purpose==
==Purpose==
The wiki technical note herein describes the desktop computer program TAPcurrents for the tidal analysis and prediction of water currents in tidal waterways. Designed to be easy to use, its Graphical User Interface (GUI) permits quick separation of a time series of water current measurements into its tidal and non-tidal components using a selective least squares harmonic reduction employing up to 35 tidal constituents. After saving the ''tidal constants ''for the constituents selected during analysis, the user can generate predictions of the ''astronomical'' ''current'', the water current that varies at known tidal frequencies attributable to gravitational interactions between the earth, moon, and sun.
The Coastal Inlets Research Program Technical Wiki herein describes the desktop computer program TAPtides for the Tidal Analysis and Prediction of water levels. Designed to be easy to use, its Graphical User Interface (GUI) permits quick separation of a time series of water level measurements into its tidal and non-tidal components using a selective least squares harmonic reduction employing up to 35 tidal constituents. After saving the ''tidal constants ''for the constituents selected during analysis, the user can generate predictions of the ''astronomical'' ''tide'', the water level that varies at known tidal frequencies attributable to gravitational interactions between the earth, moon, and sun.


==Introduction==
==Introduction==
Many software packages are available today that allow current predictions to be made in tidal waters throughout the world. With few exceptions, these programs utilize tidal constants determined by governmental agencies and the casual user of this software is generally unaware of any of the details involved in the agency<nowiki>’</nowiki>s analysis, not least the breakdown of observed water current variation into its tidal and non-tidal parts. Separating water current histories into their tidal and non-tidal components is important for two reasons. It is easy to fault the astronomical prediction formula when predictions don<nowiki>’</nowiki>t agree with observations but, depending on the region, the astronomical current may in fact be quite small compared to wind-generated and other forms of locally induced current present in the same record. Very little information is available to users about the length of the current time series used to estimate tidal constants for predictions, or about how old the data are. Predictions for coastal waterways that have undergone significant hydrologic change (storms, dredging activity) are particularly susceptible to errors resulting from inadequate or outdated current measurements. Secondly, non-tidal currents are of interest in their own right, particularly in estuaries where gravitational circulation plays an important role in the transport of water-borne materials.
Many software packages are available today that allow tide predictions to be made in tidal waterways throughout the world. With few exceptions, these programs use tidal constants determined by governmental agencies and the casual user of this software is generally unaware of any of the details involved in the analysis, not least the breakdown of observed water level variation into its tidal and non-tidal parts.
 
 
In many cases, little information is available to users on the length, quality or age of the water level time series used to estimate tidal constants. Predictions for coastal waterways that have undergone significant hydrologic change (storms, dredging activity) may be subject to errors resulting from outdated measurements. The software presented here gives users the ability to make tidal harmonic predictions where suitable data are available for calculating the tidal harmonic constituents.
 


With the introduction of acoustic Doppler current monitoring devices, both governmental and non-governmental organizations have begun to acquire much more data than ever before. TAPcurrents is the ideal package with which to explore and develop preliminary to finalized current information from serial records spanning several weeks to several months. Although its operating features are intuitive and can be quickly grasped by users familiar with MS Windows<sup>®</sup> terminology, it is important to have a general understanding of the theory of tides and currents before using TAPcurrents. Comprehensive references such as Cartwright (2000) and Pugh (2004) are highly recommended for this purpose, as is Boon (2004) for a practical introduction.
TAPtides is the ideal package to explore and develop preliminary or finalized tidal predictions from serial records spanning several weeks to several months. Although its operating features are intuitive and can be quickly grasped by users familiar with MS Windows<sup>®</sup> terminology, it is important to have a general understanding of the theory of tides before using TAPtides. Comprehensive references such as Cartwright (2000) and Pugh (2004) are highly recommended for this purpose, as is Boon (2004) for a practical introduction.


==Installation==
==Installation==
To run TAPcurrents the MATLAB Component Runtime (MCR) program must first be installed using the MCRInstaller provided with the application package. When installing SMS select the option to install TAPtides and TAPcurrents. After unzipping the package in a working directory, right-click the TAPcurrents program icon to create a shortcut and place it on your desktop. Run the application by double-clicking on the icon: This will create a new folder with the required MCR programs.
To run TAPtides the MATLAB Component Runtime (MCR) program must first be installed using the MCRInstaller provided with the application package. When installing SMS select the option to install TAPtides and TAPcurrents. After unzipping the package in a working directory, right-click the TAPtides program icon to create a shortcut and place it on your desktop. Run the application by double-clicking on the icon: This will create a new folder with the required MCR programs. TAPtides is programmed in the MATLAB<sup>®</sup> technical computing language, a product of The MathWorks, Inc. The present program is compatible personal computers with the MS Windows operating system (Windows XP).
 
==Overview==
The TAPtides menu has two options ''Tidal'' ''Analysis'' and ''Tidal Prediction''. The last two buttons launch programs to conduct water level analysis (TIDAL ANALYSIS) and generate tide predictions respectively (CHOOSING TIDAL CONSTITUENTS, TIDAL PREDICTION). The analysis portion of the software accepts several file types (see INPUT FILES). The files used in this CHETN are automatically downloaded during the installation process and are located within the TAPtides folder which is located in the SMS directory. The tidal prediction portion of the software requires tidal constituents (amplitudes and phases of individual tidal components) from the tidal analysis program.
 
==Tidal Analysis ==
[[Image:TAPtides_Figure1v2.PNG|thumb|right|600px|Figure 1. TAPtides Analysis Page.]]
The method used by TAPtides to analyze a water level time series is commonly known as Harmonic Analysis, Method of Least Squares (HAMELS). It achieves a progressive reduction in variance (mean square deviation about the mean) by adding harmonic terms with specific astronomical frequencies to a general least squares model of the type used for multiple regression. It is not Fourier analysis, a procedure that employs only the Fourier frequencies. A brief description of HAMELS is given in Appendix B. For a complete description of the least squares harmonic analysis method employed here, the reader is referred to Boon (2004).
 
 
It is preferable to use the term ''water level analysis'', rather than tide analysis, because the measured change in water level in coastal waterways varies at both tidal and non-tidal frequencies, including frequencies so low they appear as a static level or linear trend in short series. The objective of the analysis is to separate these components so that a ''tidal height prediction'' can be made with the component that is predictable – the water level that oscillates at tidal frequencies. To perform a water level harmonic analysis, click on the <nowiki>’</nowki>Tidal Analysis<nowiki>’</nowiki> button within the TAPtides window.
 
 
Clicking the ''Tidal'' ''Analysis'' button within the SMS menu ''Tools<nowiki>|</nowiki>Harmonic Analysis'' starts the GUI page that performs tide analysis (see Figure 1). It is recommended that the user click on the ''Disclaimer'' menu at the top of the window and read the disclaimer message before proceeding. Click the ''Program Help'' menu immediately to the left of the ''Disclaimer'' button to view information about input files, file analysis, selection of tidal constituents and other topics.
 
<br style="clear:both" />
 
The analysis occurs in two steps:
 
# Settings and File Selection: Enter time series length (in days) and water level units (meters or feet). If the series length is left empty the total duration of the imported file will be used. If a number is entered that is larger than the input series length, a warning message will occur and the series length will be reduced automatically. Select a data file for analysis using the appropriate press button in the upper right corner of the page. Pressing a button will open a file browser displaying only files of the indicated type (MS Excel files with .xls extension or ascii text files with .tsd extension). Select a file and press the open button in the browser.  If the print log enabled box is checked, a text file will be generated containing the parameters selected and other information from the analysis.
# Analysis: After the file is loaded, the message ''File ready for analysis'' will appear in the data box directly below the file selection buttons and the large ''Analyze'' button will turn green Pressing the ''ANALYZE'' button will start the analysis. The number of days in the file selected will be briefly displayed in the data box, followed by the date and time of the first record in the file and the file name. A graph will appear next showing the results of a least squares harmonic analysis fitting the five main tidal constituents, O1, K1, N2, M2 and S2, to the water level data (Figure 2). A list box at the bottom of the page displays the ''tidal'' ''constants'' (amplitude and phase) computed for all five constituents.
 
 
The check boxes in the center of the window indicate the tidal constituents available  for harmonic analysis. Initially, only five major constituents are activated (shown in red text). The first five are always selected but the thirty others should be thought of as potential constituents that may be included in subsequent rounds of analysis. To include additional constituents, click on the check boxes for individual constituents and press the ''ANALYZE'' button. Selecting the proper constituents is explained in the next section.
 
 
For a relatively short time series of water levels (29 days to 58 days), there are limits to the number of constituents that can be used in a harmonic analysis. In general, the difficulty caused by short time series arises from the resolution of certain constituents that are close to others in frequency (consult the list box at the top of the Analysis page for a list of available constituents and their frequency). The main solar semidiurnal constituent S2, for example, has a frequency of exactly 2 cycles per mean solar day (cpd); the semidiurnal constituents T2 (1.9973 cpd), R2 (2.0027 cpd) and K2 (2.0055 cpd) are all very close to this frequency and can be difficult to resolve from a short series. The minimum series duration ''T'' necessary to fully resolve two tidal frequencies ''f''<sub>1</sub> and ''f''<sub>2</sub> is given by ''T'' =1/<nowiki>|</nowiki>''f''<sub>1</sub>''-f''<sub>2</sub><nowiki>|</nowiki>, the synodic period. The synodic period for S2 and K2, for example, is 1/0.0055 or 181.8 days. Another important aspect to consider is the number of constituents chosen to model the tide. The user should start with the default constituents and choose additional constituents on the basis of their ability to reduce residual variance without violating the synodic period rule. Likely candidates will be found using the'' high'' ''band periodogram'' to examine the total distribution of variance (energy) with frequency. The periodogram feature is further explained below.
 
===Three-day Plot===
During analysis, the three-day'' ''plot'' ''feature in the gray frame on the upper left side of the TAPtides window may be used to closely examine three-day periods of the time series. Like the main plot which appears after pressing the ANALYZE button, the 3-day plot uses Julian days to display time (the corresponding calendar date is also displayed for convenience). The three-day plot of observed (red), predicted (blue) and residual (green) water level gives a wave-by-wave view showing how well the tidal harmonic model fits the data. A flat residual line indicates a good fit. If the predicted (blue) curve shows double peaks where the observed (red) curve only has single peaks, this may be an indication that too many tidal constituents are being used.
 
 
Another good reason to use the three-day plot is to investigate errors; e.g., dropped data points, vertical datum shift, or a shift to incorrect times. The least squares algorithm used in TAPtides is not affected by small data gaps (provided the time stamping remains correct). Although a short gap may be acceptable, the program will still issue a warning if the number of observations found is less than the number expected based on the series length specified and the calculated sampling rate based on the first two recorded sample times in the data series.
 
===Additional Tools===
Several tools are provided to assist the user in choosing constituents for inclusion in a harmonic model of the astronomical tide. Rather than relying on any single one of these tools, the user should use them in combination while keeping the series length in mind. Following a brief description of the available tools listed below, two examples of the recommended tidal analysis procedure are presented to illustrate their use.


TAPcurrents is programmed in the MATLAB<sup>®</sup> technical computing language, a product of The MathWorks, Inc. The present program is an executable version compatible with personal computers using the MS Windows operating system (Windows XP).
===Residual Periodogram===
The residual periodogram is a line spectrum depicting the distribution of residual (measured minus predicted) energy at the Fourier frequencies. Fourier frequencies are multiples of the fundamental frequency 1/T and thus may not coincide with the tidal frequencies which, with the exception of the overtides (S4, S6, M4, M6, M8), are not multiples of any given frequency. However, with increasing series length Fourier frequencies become more numerous and bandwidth decreases, resulting in closer approximations to tidal frequencies. Using the data cursor in the MATLAB figure containing the ''high band'' ''periodogram'' (1-8 cpd), the user can determine the frequencies associated with the highest spectral peaks and look for the closest match to one of the tidal frequencies shown in the list box at the top of the analysis page, checking the appropriate box for the constituent indicated. At this point the user should consider each new constituent as only a candidate for inclusion in the tidal model, to be verified in subsequent analysis. Note that much of the residual variance displayed in any one periodogram may well be due to non-tidal meteorological forcing.


==Data Formats==
TAPcurrents accepts input data in either text format or Microsoft Excel format. The Excel format is recommended for users who collect original data from a variety of sources and require a platform that is convenient for manual data entry and editing (units conversion, date and time corrections, quality control parameters). The Excel workbook also provides multiple worksheets for inclusion of header information with location, sensor parameters, depth and other attributes of a self-describing data set. A text format is provided for a process-controlled data stream produced by the user<nowiki>’</nowiki>s own application.


===Entering data with Excel===
For convenience, both a ''high band periodogram'' (1 to 8 cpd) and a ''low band periodogram'' (0 to 3 cpd) are provided. The high band periodogram is well-suited for examining intertidal energy associated with transient events (e.g., storm surge). The low band feature can be used to examine subtidal oscillations that are usually associated with low frequency extratropical forcing. Subtidal energy (variance) in particular can be large compared to the tidal energy at certain locations. In those instances harmonic analysis will account for a low percentage of the total variance regardless of the number of tidal constituents used. Likewise the harmonic model of the tide cannot be deemed to have "failed" for this reason since it is designed to predict only the water level change occurring at tidal frequencies.
TAPcurrents input files may use an array of water current data entered on the first worksheet of a Microsoft Excel workbook with file extension .xls. Only files with this extension will appear when the <nowiki>’</nowiki>SELECT .xls file<nowiki>’</nowiki> button is pressed with the TAPcurrents Analysis page active (Fig. 1). Two Excel formats are available:                                                                           


:1. Polar format: current speed and direction                     
===RMS Error and Percent Reduction in Variance===
::Col. 1 - Date in Excel month-day-year format (mm/dd/yyyy)         
Two statistical parameters are provided near the center of the ''Analysis'' window to assist the user in evaluating the degree of success achieved by the model in representing the data. The RMS error, calculated as the square root of the mean square difference between observed and predicted water levels, is a measure of the expected error associated with an individual water level prediction. The Percent Reduction in Variance (''%R_Var'') is the percentage of the total variance in water level explained by the astronomical tide model. Ideally, inclusion in the model of any one constituent suggested by the periodogram should result in a noticeable ''decrease ''in RMS error combined with an ''increase'' in ''%R_Var''. Again, if the data are taken from a region with strong meteorological forcing in relation to the tidal regime, it will not be possible to achieve either a high ''%R_Var'' or a low RMS error.
::Col. 2 - Local Standard Time using Excel 24-hour format
::*Col. 2 (Optional) Date&Time in Excel format: mm/dd/yy hh:mm
::Col. 3 - any non-numeric (e.g., 3-letter time zone label)         
::Col. 4 - Current speed in meters per second or knots
::Col. 5 - Current direction in degrees 0-360 relative to true north


:2. Vector format: east-west, north-south current speed components
===Constituent Amplitude and Phase Estimates===
::Col. 1 - Record number or profile number (numeric field)
After conducting an analysis with a new tidal constituent added to the model, the user should check the amplitude found for that constituent in the list box at the bottom of the ''Analysis'' window. It should exceed at least one percent of the largest major constituent amplitude. More importantly for a short series, it should not cause another constituent at an adjacent frequency to change either its amplitude or phase by more than a few percent (K2 and S2 may be exceptions). When this occurs, it indicates that the harmonic model derived will yield erroneous future predictions even though the present fit to the observed water level data appears good in all other respects.
::Col. 2 – Date & Time in Excel format: mm/dd/yy hh:mm
::Col. 3 – U (east-west) current component (meters/sec or knots)
::Col. 4 – V (north-south) current component (same per choice above)


*If serial date and time is used in column 2, a numeric value (e.g., Julian day) can be entered in column 1. A set of non-numeric column labels may be inserted as the first row of either array. Note that a 5th column is not allowed when using the vector format.
===Tidal Form Number===
This number indicates the relative dominance of semidiurnal and diurnal tides. It is calculated as F = (K<sub>1</sub><nowiki>+</nowiki>O<sub>1</sub>)/(M<sub>2</sub><nowiki>+</nowiki>S<sub>2</sub>) where the constituent names represent their respective amplitudes. The tides can be described as semidiurnal for F<nowiki><</nowiki>0.25, mixed semidiurnal for 0.25<nowiki>></nowiki>F<nowiki>></nowiki>1.5, mixed diurnal for 1.5<nowiki>></nowiki>F<nowiki>></nowiki>3.0, and diurnal for F<nowiki>></nowiki>3.0.


===Entering data in Text Format===
===Analysis in Stages===
After pressing the button marked <nowiki>’</nowiki>SELECT .tsd file<nowiki>’</nowiki> while the TAPcurrents Analysis page is active, the user may use the browser to open a three-column ascii file containing either current speed (m/sec) and direction (degrees from true north) or U,V current components. TAPcurrents makes a determination based on the information contained in the second header string shown in double quotes below. Note that in lieu of time, the series utilizes a time offset in seconds after the starting date and time indicated in the third header string in double quotes. The two input formats for vector data are shown below
To proceed with an analysis, the user should work in stages starting with the five major constituents (O1, K1, N2, M2, S2), as Stage I. After pressing the radiobutton to select the high band periodogram, proceed with the following steps:


:TIME_SERIES
# Using the data cursor, identify the peak frequencies shown in the residual periodogram and match them to the nearest tidal frequency shown in the list box. In most cases, the ''Fourier'' frequencies will not match the tidal frequencies exactly for the reasons previously given
:"May 1, 2008"  "Velocity - Mag. & Dir."    3    41  "05/01/2008 12:00:00"
# Check the boxes of constituent(s) selected above as candidates for Stage II. Constituents of different type classes (diurnal, semidiurnal, etc.) may be included in one stage but several constituents within the same class that are adjacent in frequency should not be included together.
:0.0              1.0            -75.0
# With the high band radiobutton remaining on, press ANALYZE to begin Stage II.
:900.0              1.1            -70.0
# Verify the constituent(s) selected as model candidates in the previous stage by confirming (1) peak elimination in the residual periodogram, (2) appropriate size for the resulting constituent amplitude as displayed in the lowermost list box, (3) decreased RMS error, increased %R_Var. Uncheck the constituent if it clearly fails any of these tests. Otherwise, the new stage will be marked by a periodogram showing new residual peaks at a lower energy level. To amplify the remaining peaks at each new stage, the y-coordinate scale expands as the energy level drops.
:1800.0              1.2           -65.0
# Select constituent candidates as before for Stage III. Continue this process until all constituents that can be successfully matched to a residual peak frequency are found and included in the astronomical tide model.
:2700.0              1.3           -60.0
:3600.0              1.4            -55.0
:4500.0              1.5            -50.0
:5400.0              1.6            -45.0
:6300.0              1.7            -40.0


When analyzing a short series (58 days or less), look for signs of poor resolution between neighboring constituents on the frequency scale. This usually takes the form of a large change in amplitude and phase for such constituents when analyzed jointly versus separately. For tides of small range especially, selecting a constituent that is very close in frequency to one of the major constituents in a short series should be avoided; e.g., T2 (1.9973 cpd) and R2 (2.0027 cpd) adjacent to S2 (2.0000 cpd).


:TIME_SERIES
===Seasonal Constituents===
:"Current Buoy 1"  "Velocity - Components"  3  4376  "03/06/2003 14:45:00"
The ''Analysis'' window contains four data boxes on the left side with zero values entered in blue. They allow the user to manually enter an amplitude and phase for the solar annual (Sa) and solar semiannual (Ssa) tide constituents (optional). These numbers are available for most primary tide stations in the United States and can be applied at nearby stations as well. Otherwise, several years of observations are required to determine Sa and Ssa, the so-called ''seasonal tides''.
:600.00      -0.494      0.03
:1200.00    -0.525      0.052
:1800.00    -0.546      0.06
:2400.00    -0.542      0.051
:3000.00    -0.576      0.058
:3600.00    -0.6        0.073
:4200.00    -0.601      0.069
:4800.00    -0.597      0.058


==Overview==
===Vertical Datums===
The TAPcurrents menu has two options: ''Tidal'' ''Analysis'' and ''Tidal Prediction''. The last two buttons launch programs to conduct water current analysis (TIDAL ANALYSIS) and generate tidal current predictions respectively (CHOOSING TIDAL CONSTITUENTS, TIDAL PREDICTION). The analysis portion of the software accepts several file types (see INPUT FILES). The files used in this CHETN are automatically downloaded during the installation process and are located within the TAPcurrents folder which is located in the SMS directory. The tidal prediction portion of the software requires tidal constituents (amplitudes and phases of individual tidal components) from the tidal analysis program.
TAPtides analysis adopts the vertical reference of the user<nowiki>’</nowiki>s data in all of its calculations. TAPtides predictions are normally made relative to mean sea level (MSL) but provide the option of generating predictions relative to Lowest Astronomical Tide (LAT), a tidal datum commonly used outside the United States. Unlike other tidal datums that require a lengthy tabulation of observed high and low water heights, LAT is derived as the ''lowest'' predicted tide over a 19-year lunar node cycle and thus depends entirely on the accepted tidal constants for the station involved. A similar datum, Highest Astronomical Tide (HAT), is derived as the ''highest'' predicted tide over the same interval. <u>Both datums</u> <u>are computed as offsets from MSL</u>. The numbers appearing in the datum offset boxes on the analysis page are saved with the tidal constants used in making tidal predictions (see TIDE PREDICTIONS). If the blue numbers that initially appear are left at zero, tidal predictions will be generated relative to MSL; otherwise, by entering a ''negative'' number to indicate its offset ''below'' MSL, predictions will be made relative to LAT. To obtain offsets, check the ''compute Datums'' box in the lower right corner of the page before clicking on the ANALYZE button for the final analysis. When this box is checked the program internally performs 19 years of predictions to find and display the HAT and LAT offsets relative to MSL. <u>Caution</u>: Use a water level record of at least 180 days duration to obtain tidal constants for reliable datum determinations.


==Current Analysis==
===Printing to file===
The method used by TAPtides to analyze a water current time series is commonly known as Harmonic Analysis, Method of Least Squares (HAMELS). It achieves a progressive reduction in variance (mean square deviation about the mean) by adding harmonic terms with specific astronomical frequencies to a general least squares model of the type used for multiple regression. It is not Fourier analysis, a procedure that employs only the Fourier frequencies. A brief description of HAMELS is given in Appendix B. For a complete description of the least squares harmonic analysis method employed here, the reader is referred to Boon (2004). Note that it is preferable to use the term ''water current analysis'', rather than tide analysis, because the measured water currents in coastal waterways vary at both tidal and non-tidal frequencies. The objective of the analysis is to separate these components so that a ''tidal current prediction'' can be made with the component that is predictable – the water current that oscillates at tidal frequencies. Clicking the ''Current Analysis'' button within the SMS menu ''Tools<nowiki>|</nowiki>Harmonic Analysis'' starts the GUI page that performs water current analysis (see Fig. 1). It is recommended that the user click the ''Disclaimer'' menu at the top of the window and read the disclaimer message before proceeding. Click the ''Program Help'' menu immediately to the left of the ''Disclaimer'' button to view information about input files, file analysis, selection of tidal constituents and other topics. The analysis can then be undertaken with the following steps:
After checking the ''enable print to file'' check box, pressing the ANALYZE button will save a listing of the observed, predicted and residual water levels in a text file (*.txt) with the same name as the input Excel file.


===Settings and Selections===
===Saving Results===
Check the appropriate ''units box'' (meters per second or knots) and press the file selection button to choose a data file in either the Excel (.xls) or text file format (.tsd). Using the browser, open one of the example files included with TAPcurrents and wait for the file to load and data graphics to appear. The main graphic that appears will contain a scatterplot of the U (east-west) and V (north-south) current components and the Principal Current Axis (PCA) of maximum variance<ref>In multivariate analysis, the coordinate axis for the variable containing maximum variance.</ref> displayed as a blue line passing through the bivariate mean <nowiki>[</nowiki>Um,Vm<nowiki>]</nowiki>.  Reciprocal headings for this axis may be viewed on the graphic as well as the flood and ebb direction boxes on the analysis page (Fig. 1). Normally the user will choose the heading corresponding to the flood direction and enter it in the edit box above the check box labeled <nowiki>’</nowiki>Lock headings<nowiki>’</nowiki>, although another flood heading could be chosen as well (e.g., a channel axis). After entry, check <nowiki>’</nowiki>Lock Headings<nowiki>’</nowiki>.
Once, a satisfactory tidal analysis is obtained, the results may be saved in a binary MATLAB data file. The variables stored in this file may be examined using the MATLAB load command by entering a file name (<u>without</u> the .mat extension) in the data entry box in the lower left corner and pressing SAVE.


[[Image:CHETN_TAPcurrents_15Oct08_03.png|framed|Figure 1. TAPcurrents Analysis Page.]]
==Input Files==
The TAPtides analysis tool accepts two file types containing input water level time series. The first is a Microsoft Excel Workbook (*.xls) or TAP Excel File. The web services utility, described in Appendix A, allows users to directly download water level data from active NOAA stations and output the data in TAP Microsoft Excel Worksheet files. The second file format allowed in TAP is the SMS Time Series Data file (*.tsd) or tsd file. The Time Series Data files are useful file format because they can easily be imported into SMS for viewing, model forcing and comparison with model results. Other file formats such as the SMS XY Series files and generic ASCII files may be converted to TAP Excel files or tsd files using the utility Filter1D also provided and optional installation software in SMS 10.1<nowiki>+</nowiki>.


===Lock Headings=== This step initiates a rotation of the U,V current axes about the U,V bivariate mean (black cross in Fig. 2) to align with the new heading. The rotation therein produces new orthogonal components, Up and Vp, in which Up readings along the major axis are positive in the flood direction and negative in the ebb direction. The ANALYZE button will turn green when ready to analyze Up as the variable with the largest part of the total variance (98.7% as shown in the Axis Variance text box in Fig. 1). Although the minor axis current Vp is ignored, this variable accounts for only 1.3% of the total variance in this case – not a large loss of information. Choosing Up, on the other hand, reduces the spatial dimensions of the plotting problem from two to one, thus allowing a visually informative current curve to be constructed in place of a vector diagram or a table of numbers. The ability to view the current curve in detail will be especially useful in the next stage of the analysis.
===Time Series Data File===
The second file format which is supported in the analysis page of TAPtides is the Time Series Data file (*.tsd). This file is supported in SMS versions 10.1<nowiki>+</nowiki>. The ASCII file consists of two header lines followed by data columns separated by spaced or tabs. The first line contains the identifier TIMESERIES. The second line contains 5 elements. The first element is the name of the time series within apostrophes. The second element specifies the curve type and may be one of: "Unassigned", "Vel. & Mag.", or "Vel. Components". The third element is an integer specifying the number of input columns including the time stamp (column 1). The forth element is the length of the input time series. The fifth element is a reference date and time of the first data point. The date and time are specified as "mm/dd/yyy HH:MM:SS" where mm is the month, dd is the day, HH is the hour, MM is the minute, and SS is the seconds. The input time series does not need to have a regular time interval.


[[Image:CHETN_TAPcurrents_15Oct08_04.png|framed|Figure 2. U,V scatterplot]]
:TIME_SERIES<br>
:"CRCR2007"  "Unassigned"  2  1535  "03/01/2007 00:00:00"<br>
:0.00          0.227<br>
:1800.00          0.198<br>
:3600.00          0.168<br>
:5400.00          0.137<br>
:7200.00          0.104<br>
:9000.00          0.070<br>
:10800.00          0.036<br>


===Analyze currents===
The third step begins after pressing the large ANALYZE button on the right side of the page (Fig. 1). A new graph will quickly appear showing the results of a least squares harmonic analysis fitting the five main tidal constituents, O1, K1, N2, M2 and S2, to the Up current data. A listbox at the bottom of the page displays the ''tidal'' ''constants'' (amplitude and phase) computed for all five current constituents. The five symbols appear next to checked boxes inside a wide gray frame containing thirty more boxes left unchecked. The first five are always selected but the thirty others should be thought of as potential constituents that can be chosen for inclusion in the next round of analysis. After checking additional constituents, the ANALYZE button may be pressed again to perform another analysis.


===Select constituents===
===TAP Microsoft Excel Worksheet.===
Different regions have different tidal types which affects the number and importance of the tidal constituents represented in the current. The user must identify these constituents guided by the analytical tools provided in the Analysis GUI while recognizing that, for a relatively short series of observations (29 days to 58 days), there are limits to the number of tidal constituents that can be successfully resolved. In general, the difficulty caused by short series length arises in the resolution of certain constituents that are close to others in frequency (consult the list box at the top of the Analysis page for a list of available constituents and their frequency). The major solar semidiurnal constituent S2, for example, has a frequency of exactly 2 cycles per mean solar day (cpd); the semidiurnal constituents T2 (1.9973 cpd), R2 (2.0027 cpd) and K2 (2.0055 cpd) are all very close to this frequency and can be difficult to resolve in a short series.
These files consist of an array of water level data entered on the first worksheet of a Microsoft Excel workbook (*.xls). The first line of the worksheet is reserved as a header line usually used to describe data columns. Two separate formats are available for data entry in the subsequent rows:


The minimum series duration ''T'' necessary to fully resolve two tidal frequencies ''f''<sub>1</sub> and ''f''<sub>2</sub> is given by ''T'' =1/<nowiki>|</nowiki>''f''<sub>1</sub>''-f''<sub>2</sub><nowiki>|</nowiki>, the synodic period. The synodic period for S2 and K2, for example, is 1/0.0055 or 181.8 days. Another important aspect to consider is the number of constituents chosen to model the tide. The user should start with the default constituents and carefully choose additional constituents on the basis of their ability to reduce residual variance without violating the synodic period rule. Likely candidates will be found using the'' high'' ''band periodogram'' to examine the total distribution of variance (energy) with frequency. The periodogram feature is further explained below.
{|border="0" cellspacing="0" width="100%"
|&nbsp;
|A.
|Col. 1 - Record number, station number or Julian day (not used in calculations)     
|-
|&nbsp;
|&nbsp;
|Col. 2 - Date in Excel month-day-year-time format (3/14/01 13:30)
|-
|&nbsp;
|&nbsp;
|Col. 3 – Water level in feet or meters (Columns <nowiki>></nowiki> 3 must be empty)       
|-
|&nbsp;
|B.
|Col. 1 - Record number, station number or Julian day (not used in calculations)
|-
|&nbsp;
|&nbsp;
|Col. 2 - Date in Excel month-day-year format (3/14/01)
|-
|&nbsp;
|&nbsp;
|Col. 3 - Local Standard Time in Excel 24-hour time format (13:30)
|-
|&nbsp;
|&nbsp;
|Col. 4 – Water level in meters or feet
|}


===3-day plot ===
A set of non-numeric column labels may be inserted as the first row of either array. Note that a 4<sup>th</sup> column is not allowed when using format A.
After selecting constituents, the ''3-day plot ''feature in the gray frame on the upper left side of the page can be very helpful. Like the main plot that appears after pressing the ANALYZE button, the 3-day plot uses Julian days to display time and select a time interval for plotting (the corresponding calendar date is also displayed for convenience). The 3-day plot of observed (red), predicted (blue) and residual (green) current gives a wave-by-wave view showing how well the tidal harmonic model fits the data. Obviously, the fit is very good if the residual is almost a flat line. However, when it is not and the blue curve starts showing double peaks while the red curve has only single peaks, this may be a further indication of the problem of trying too many tidal constituents with too little data.


Of course another reason to use the 3-day plot is to investigate errors; e.g., dropped data points, current speed shifts, or a shift to incorrect times. The least squares algorithm used in TAPcurrents is not affected by small data gaps, provided the time remains correct. This is one reason the data are entered in a multi-column spreadsheet – the user may check that every bivariate current reading is associated with the correct serial date and time. Although short gaps are acceptable, the program will still issue a warning if the number of observations found is less than the number expected based on the series length specified and the calculated sampling rate. TAPcurrents determines sampling rate from the first two recorded sample times in the data series.
Additional metadata such as instrument type, location etc. should be stored in separate worksheets.


===Using the Residual Periodogram===  
===Pre-set constituent selection===
A special tool for use in choosing constituents to include in a current analysis is the residual periodogram. While not infallible, the Fourier periodogram can often identify important tidal current constituents among energy peaks representing oscillations left out of the model – left out but still present in the residual. For convenience, both a ''high band periodogram'' (1 to 8 cpd) and a ''low band periodogram'' (0 to 3 cpd) are provided. The high band periodogram is used most often for constituent identification; the low band feature can be used to characterize subtidal oscillations that are usually associated with meteorological forcing (wind stress, atmospheric pressure change).
To avoid having to check multiple constituent symbol boxes each time the user repeats a tidal analysis, a worksheet named ''tidecn ''may be added to the Excel file after the first worksheet containing the water level data. This worksheet must contain the list of symbols for TAPtides<nowiki>’</nowiki> 37 tidal constituents (including Sa and Ssa) in the first column of the ''tidecn'' worksheet in order of increasing frequency moving downward. Enter the amplitude and phase of Sa and Ssa, if known, in the second and third columns; otherwise enter zeros. For the remaining constituents, enter <nowiki>’</nowiki>1<nowiki>’</nowiki> or <nowiki>’</nowiki>0<nowiki>’</nowiki> in the second column to indicate symbols to be automatically checked or unchecked once the file has been loaded; enter a zero in the third column. An example of the ''tidecn'' worksheet can be found in Excel file ''SWPT20070101R6m.xls''.


===Using RMS Error and Percent Reduction in Variance===
===Tidal datums===
Two statistical parameters are provided near the center of the Analysis page to assist the user in evaluating the degree of success achieved by the model in representing the data. The RMS error, calculated as the square root of the mean square difference between observed and predicted water currents, is a measure of the expected error associated with an individual current prediction. The Percent Reduction in Variance (%R_Var) is the percentage of the Up variance in water current explained by the astronomical model. Ideally, inclusion in the model of any one constituent suggested by the periodogram should result in a noticeable ''decrease ''in RMS error combined with an ''increase'' in %R_Var.  However, if the data are taken from a region with strong meteorological forcing in relation to the current regime, a high %R_Var and a low RMS error may be impossible to achieve.
To display the position of vertical datums on monthly (30-day) water level plots, enter datum elevations in a new worksheet named ''datums'', placing this tab in any position after the first worksheet in the Excel workbook with one of the formats in Table 1.


===Using Constituent Amplitude and Phase Estimates===
Table 1. Formats allows for datums worksheet.
After conducting an analysis with a new tidal constituent added to the model, first check the amplitude found for that constituent in the listbox at the bottom of the page. It should exceed at least one percent of the largest major constituent amplitude. More importantly for a short series, it should not cause another constituent at an adjacent frequency to change either its amplitude or phase by more than a few percent (K2 and S2 may be exceptions).
{|border="2" cellspacing="0"  width="59%"
|align = "center" colspan = "3"|a. U.S. format
|align = "center"|&nbsp;
|align = "center"|b. Non-U.S. format
|-
|Datum
|align = "center"|Elev.(ft)
|align = "center"|&nbsp;
|Datum
|align = "center"|Elev.(m)
|-
|plotmax
|align = "center"|6.00
|align = "center"|&nbsp;
|plotmax
|align = "center"|3.00
|-
|HAT
|align = "center"|3.53
|align = "center"|&nbsp;
|HAT
|align = "center"|2.47
|-
|MHHW
|align = "center"|2.76
|align = "center"|&nbsp;
|MSL
|align = "center"|0.00
|-
|MSL
|align = "center"|1.35
|align = "center"|&nbsp;
|STND
|align = "center"|0.00
|-
|MLLW
|align = "center"|0.00
|align = "center"|&nbsp;
|LAT
|align = "center"|<nowiki>-</nowiki>2.51
|-
|LAT
|align = "center"|<nowiki>-</nowiki>0.69
|align = "center"|&nbsp;
|plotmin
|align = "center"|<nowiki>-</nowiki>3.00
|-
|plotmin
|align = "center"|<nowiki>-</nowiki>2.00
|align = "center" colspan = "3"|&nbsp;
|}


===Analysis in Stages===
STND is the station datum or the zero point of the measurement scale in use (in feet or meters). If MSL in relation to the station datum is unknown, it should be set to zero.
To proceed with an analysis, work in stages starting with the high band periodogram and the five major constituents (O1, K1, N2, M2, S2) as Stage I. Use the MATLAB ''data cursor'' to obtain the frequency of the highest peaks in the periodogram, treating the y-coordinate, ''energy'',  as a relative measure of importance<ref>In the absence of band-averaging, frequency intervals are small but energy estimation errors are large. </ref>. Proceed with the analysis in stages as follows:


I. Check the boxes of the constituents with highest energy as model candidates for Stage II. Include constituents of different tidal types (diurnal, semidiurnal, etc.) in one stage but do not include several constituents of the same type that are adjacent in frequency. For tidal type, note the amplitudes of the five constituents in stage I.
After a few seconds, the main TAPtides window will appear with four program choices: ''coopsVhr'', ''coopsR6m'', ''Tide Analysis'', and ''Tide Prediction''. The first two buttons allow the user to quickly download verified hourly heights (coopsVhr) or raw six-minute heights (coopsR6m) from the National Oceanographic and Atmospheric Administration (NOAA) network of active tide stations.


II. With the high band radiobutton on, press ANALYZE to begin Stage II. Verify the constituent(s) selected as model candidates in the previous stage by confirming ''peak elimination'' in the residual periodogram and ''size'' of the resulting constituent amplitude as well as ''fit statistics'' (RMS error, %R_Var). Uncheck the constituent if it clearly fails these tests. Otherwise, the new stage will be marked by a periodogram showing new residual peaks at a lower energy level. Note that the y-coordinate scale expands as the energy level drops, amplifying the remaining peaks.
==Examples==
Two example data sets are presented below. Both contain water levels record in meters, the default setting for TAPtides analysis. The edit box appearing above the units selection will initially appear blank. After the input file has been selected and read, the number of days available in the file will be displayed. The user may change this setting to a lesser number but not less than 14 days.


III. Select constituent candidates as before for Stage III. Continue this process until all constituents with a significant amplitude and proper fit statistics are found and included in the astronomical current model.
=== Ballyheige, Ireland===
[[Image:TAPtides_Figure2.PNG|thumb|right|600px|Figure 2. Analyzed water level at Ballyheige (series mean level: -0.206m).]]
The first example is from Ballyheige, a town at the entrance to the Shannon River in western Ireland (''bally20040607.xls''). To get a feel for the use of the features described above, the reader can run a 30-day analysis of input file ''bally20040607.xls which contains'' water levels sampled at 5-minute intervals at Ballyheige (Data supplied courtesy of the Irish Geological Survey, Dublin, Ireland). After selecting this file the data box will display the number of days in the file followed by the date and time of the first record and the file name. After it has turned green, press the ANALYZE button to begin the analysis.


When analyzing a short series (58 days or less), watch for signs of a failed resolution between neighboring constituents on the frequency scale. This usually takes the form of a large change in amplitude and phase for such constituents when analyzed jointly versus separately. For currents of small range especially, avoid selecting a constituent that is very close in frequency to one of the major constituents in a short series; e.g., T2 (1.9973 cpd) and R2 (2.0027 cpd) adjacent to S2 (2.0000 cpd).


==Saving Harmonic Constants==
A window graph will appear displaying the ''observed water level'' (red), the ''astronomic tide'' (blue) and the ''residual'' (green) or difference between observed and predicted.. A pop-up message should also appear indicating a data gap within the file (8,340 records  found, 8,353 expected). Whenever this message is seen, the cause should be sought by examining the input file. The gap in this example is too small to be seen in the 30-day plot. Using the 3-day plot feature, the gap can be clearly seen mid-morning on Julian day 173 (21-Jun-2004) at the point where the red curve abruptly shifts to the right by one hour. This is a ''time shift ''rather than a simple data gap and it means that all of the times past this point must be reduced by one hour. To skip the correction and proceed with the analysis, open the Excel file and move the worksheet labeled <nowiki>’</nowiki>Fixed_file<nowiki>’</nowiki> to the first position in the example workbook.
After the analysis is complete, the tidal harmonic constants obtained can be saved in a file for later use in generating tidal current predictions. To save a ''log file'' with the list of constituents chosen, their amplitude and phase and other information describing the analysis, check ''Enable Print to file'' (lower right, Fig. 1) before making the final run. Finally, choose a file name that is indicative of both the location and the ''depth'' at which the current observations were made. Enter the name in the large edit box (lower left, Fig. 1) and press the SAVE button. This will save the harmonic constants in a MATLAB binary file with file extension .mat. Only files of this type can be used for tidal current predictions (see TAPcurrents PREDICTIONS).


==Example Datasets==
<br style="clear:both" />
Examples of water current data are provided in the formats required for analysis with TAPcurrents. Users are encouraged to work through the examples provided to become familiar with TAPcurrents and to gain experience with  water current observations from the field.


===Example 1===
[[Image:TAPtides_Figure3v2.PNG|framed|Figure 3. High Band Periodogram.]]
To gain experience with the ''residual periodogram'', the user should first run a 29-day analysis with input file PCOA200303m15.xls (or PCOA200303m15.tsd), a data set containing currents in m/sec measured 15 m above bottom in Liverpool Bay on the eastern edge of the Irish Sea<ref>Data supplied courtesy of the Proudman Oceanographic Laboratory, Liverpool Bay Coastal Observatory  </ref>. After double clicking this file, examine the U,V scatter plot that appears and note the elliptical pattern of data points centered on the principal current axis. As previously shown in Fig. 1, the principal axis captures 98.6 percent of the total variance in U and V. Enter the principal axis heading of 96 degrees in the ''new axis / flood direction'' box, lock the heading and press ANALYZE with the high band periodogram enabled (radiobutton, frame on the right in Fig. 1). A U,V scatter plot will appear followed by the periodogram shown in Fig. 3.
After loading and reading the fixed file, run the analysis again with the high band periodogram turned on. A Fourier periodogram will appear displaying two prominent peaks at adjacent frequencies. Using the data cursor, click on the left peak. An x-axis reading of approximately 1.862 cpd should be visible. Clicking on the peak to the right, 1.966 cpd should appear (Figure 3). The first frequency falls midway between constituents 2N2 and MU2; The second midway between LAM2 and L2. For the first stage of analysis with the five major constituents, the RMS error will read  ±0.138 m and the percent reduction in variance (%R_Var) should read 98.15.


Liverpool Bay is an example of a semidiurnal current system and the amplitudes of the principal diurnal constituents, O1 and K1, are small compared to the major semidiurnal constituents N2, M2 and S2. The periodogram that appears after pressing the ANALYZE button contains one large peak with an energy of 6.4 x 10<sup>-4</sup> m<sup>2</sup>/sec<sup>2</sup> per cpd at 3.862 cpd and two smaller ones at 1.966 and 5.793 cpd. Consulting the constituent frequency listbox, the first frequency is seen to be close to the quarterdiurnal constituent M4, the second falls midway between semidiurnal constituents LAM2 and L2 and the third is near the sixth-diurnal constituent M6.  Use the MATLAB ''data cursor'' on the tool bar of the plot window and left click on the top of each peak to read its energy and frequency as shown in Fig. 3 below.


[[Image:CHETN_TAPcurrents_15Oct08_05.png|framed|Figure 3. High Band Residual Periodogram.]]
Tidal harmonic analysis is a form of ''multivariate analysis.'' To monitor the variables (constituent amplitude and phase) employed in a step-wise (stage)'' ''analysis the user should consider entering the amplitude and phase of all the constituents involved at each stage on a separate worksheet. One has already been entered in the bally20040607.xls file (tab labeled ''Stage Analysis''). Selecting all four constituents 2N2, MU2, LAM2, and L2 produces a large change in the tidal amplitudes indicating that this choice is unacceptable for a series of this length. Choosing the one constituent near each peak with the greatest amplitude will produce a better result. After selecting MU2 and LAM2, the RMS error is reduced to ±0.109 m and %R_Var is increased to 98.80 percent.


Run the analysis again with L2, M4 and M6 checked, noting their amplitudes in the listbox at the bottom of the page after the run. The amplitudes should read 0.032, 0.048 and 0.017 m/sec, respectively. These constituents should be kept as their amplitudes are reasonably large compared to N2, M2 and S2. The periodogram that will appear next for the second run now has five new peaks for the current residual at the next energy level moving down the scale.


After additional trial runs, constituents 2N2, K2, MN4, MS4 and 2MS6 also emerge as reasonable choices for inclusion in the tidal current model.
In the next stage of the analysis, the first dominant peak suggests constituents Q1 and RHO1 and the second one matches the quarter-diurnal constituent, M4. Referring again to the Stage Analysis worksheet, RHO1 and M4 emerge as the most reasonable choices, reducing the RMS error to ±0.105 m  and increasing %R_Var to 98.88 percent. In the final stage, MNS2, K2, M3, MN4, MS4 and M6 are added, reducing RMS error to ±0.100 m and increasing %R_Var to 98.98 percent. Noting the change in amplitude and phase for S2 at this stage may be surprising to some users, but in this instance it is clearly linked to relatively large amplitude in the luni-solar semidiurnal constituent, K2. K2 is often one of the major constituents in regions where the tide type is fully semidiurnal and the range is more than two meters (the mean range at Ballyheige is approximately three meters). Normally the K2 spectral peak is not pronounced in a short series because of its proximity to S2 which is included at the outset as one of the major constituents.


While adding constituents to the current prediction model, be certain to check the statistical parameters. The RMS error in the first stage at Liverpool Bay with O1, K1, N2, M2 and S2 is 0.077 m/sec and %R_Var is 97.04. These numbers change to 0.066 m/sec and 97.84% in the second stage and 0.061 m/sec and 98.19% in the third. In other words, of the 98.6% in total variance captured by the principal axis, the model can now explain 98.2 % of that variance (variance in Up) with the 13 selected constituents. A worksheet showing the constituent amplitudes and phases at each stage of the analysis is included in workbook PCOA200303m15.xls.
<br style="clear:both" />


===Example 2===
During the course of the above four stages, the peak energy shown in the periodogram falls by two orders of magnitude – from about 2 x 10<sup>-3</sup> to about 3 x 10<sup>-5</sup> m<sup>2</sup>/cpd. At this point we may enter a name and save the 15 constituents selected in a tidal constants file (e.g., ''Ballyheige_MSL'' to indicate that no offset from MSL was used).
Repeat the above steps with file RISFB200211sc.xls (Richmond, San Francisco Bay) for an example with surface current speed in knots and current direction in degrees clockwise from true north<ref>Data supplied courtesy of the U.S. National Oceanic and Atmospheric Administration,  Tides & Currents</ref>. Note that this file contains only 17 days of data as indicated in the series length data box. View the U,V scatter plot and enter a new flood heading of 331 degrees. After pressing ANALYZE,  a 15-hour data gap will be apparent in the current plot on 7Nov2002 (Julian day 311). After entering <nowiki>’</nowiki>311<nowiki>’</nowiki> for a 3-day plot, this gap will be obvious (straight lines connecting the ends of the gap are an artifact of the MATLAB line plot routine and can be ignored). There are a number of smaller (6-min) gaps in this file as well but no time shifts.


The principal axis in this example accounts for 99.2 percent of the total U,V variance. Clearly very little information is given up after choosing this axis and the user may verify that the initial run with just the five basic constituents accounts for 96.84 percent of the Up variance. Turning next to the high band periodogram to seek more constituents, the large residual peak that appears at 2.928 cpd suggests MK3. After a trial, MK3 does not look promising in terms of both its amplitude and effect on % R_Var - or the energy peak itself. A trial with M3 yields much the same result. However the next constituent down the frequency scale, 2MK3, has significant amplitude and clearly reduces the residual peak at 2.928 cpd. Adding this constituent along with K2, MS4, M6 and 2MS6 in the third stage of the analysis increases the explained variance to 97.98 percent and reduces the RMS error to 0.176 knots, leaving very little energy in the residual. Checking predicted versus observed currents with the 3-day plot feature reveals a good match in most places considering that this series, like the Liverpool Bay example, is not without its share of <nowiki>’</nowiki>noise<nowiki>’</nowiki> in the peaks of the observed current.
===Chesapeake Bay, USA===
The second example is from a water level station at the Chesapeake Bay entrance (''cbbt20021101.xls'') courtesy of the U.S. National Oceanic and Atmospheric Administration (NOAA). This example also involves a 30-day analysis of water levels. The file named ''cbbt20021101.xls'' was obtained from the NOAA ''Tides & Currents'' web site and includes hourly water level data for 30 days beginning November 1, 2002. As with the previous example, a stage analysis for this file can be found on a separate worksheet in the Excel workbook. Tidal type here is mixed, mainly semidiurnal.


===Current speed histograms===
Histograms provide information on the distribution of current speed. Mariners have long been accustomed to prediction tables that provide only the time, strength and direction of flood and ebb current maxima along with predictions of slack water times. Other professionals want to know about other aspects of the flow as well, including engineers who want to calculate fluid forces on structures, or who desire to exploit tidal power ( tidal currents) to generate electricity.


Histograms are provided on both the Analysis and the Prediction pages of TAP currents. On the Analysis page (Fig. 1), the user may select flood-and-ebb current speed distributions with frequencies given in percent of flood and ebb time. On the Predictions page (Fig. 4, Appendix B) users can make the same selections for ''monthly'' or ''yearly'' predictions with frequency given in either percent of time or in hours. In Analysis histograms, all current speeds are first reduced to their zero-mean value for the series; in Prediction histograms, current speeds include the mean, if any, transferred with the harmonic constants (see SAVING HARMONIC CONSTANTS).
Analysis in stages yields 13 constituents for this file (Q1, O1, M1, K1, J1, OO1, MNS2, MU2, N2, M2, L2, S2 and K2) but, unlike example 1, the resulting model accounts for only 71.33 percent of the variance in water level. The reason why can be clearly seen in the residual curve for the window plot of the 30-day series. During this particular month, a subtidal oscillation was present at the bay entrance whose amplitude at times exceeded the amplitude of the astronomical tide. Switching to the low band periodogram, a peak frequency is shown at 0.2069 cpd (period = 4.83 days). Although a longer analysis would improve estimates of harmonic constituents such as S2 and K2 in the astronomical tide model, the increase in %R_Var would be small compared to the subtidal energy.


Histograms generated during Analysis display both the ''observed'' and the ''predicted'' current speed distributions for the series being analyzed. The matching of these distributions can provide additional confirmation regarding choice of constituents. Analyze the RSFB file once more after checking the box the lower right corner of the page next to <nowiki>’</nowiki>enable histogram<nowiki>’</nowiki>. TAPcurrents will then generate two pairs of histograms with cumulative curves for comparison of flood and ebb zero-mean current speed distributions, predicted versus observed. To aid the comparisons, three percentile points are shown on each curve at 20%, 50% and 80%. For example, the ''observed'' San  Francisco Bay flood speeds equal or exceed 1.44 knots 20 percent of the time. For the constituents selected, 20 percent of all ''predicted'' flood currents also equal or exceed 1.44 knots over the same time interval at Richmond. The two remaining percentile levels are nearly in agreement although the cumulative curves are not identical at every point.
==Special Features==
[[Image:TAPtides_Figure4.PNG|thumb|right|600px|Figure 4. Water level history for Hampton Roads, VA, September, 2003.]]
Providing tidal constants for water level predictions is one application of TAPtides. It is also useful for informative graphs displaying monthly water level histories at active monitoring stations. Water levels in near real time are now routinely displayed at NOAA PORTS stations on the web. These contain plots typically covering the past three days showing whether observed water levels are trending above or below predicted levels. A monthly plot can add value to this product by displaying monthly and weekly variations in tidal range in relation to non-tidal events such as a transient storm surge appearing in the residual curve. An example of a monthly plot is shown in Figure 4, at the Hamptons Roads, VA water level station during Hurricane Isabel. The observed water levels are shown in red, the fitted astronomical tides in blue, and the residuals containing the storm surge component in green. These figures are useful in understanding the extreme storm tides that result from the superposition of storm surge and astronomical tides.


==TAPcurrents Predictions==
<br style="clear:both" />
Clicking the ''Tidal'' ''Current Predictions'' button within the SMS menu ''Tools<nowiki>|</nowiki>Harmonic Analysis'' starts the GUI page that performs tidal current predictions. This will bring up the TIDAL CURRENTS: PREDICTION page. Clicking the selection button will allow the user to browse for tidal constants files created during Analysis; e.g., files for the Liverpool Bay and San Francisco Bay analyses described earlier. Opening the San Francisco Bay file will initiate the GUI shown in Fig. 4.


[[Image:CHETN_TAPcurrents_15Oct08_06.png|framed|Figure 4. Tidal Current Prediction GUI.]]
==Tidal Predictions==
[[Image:TAPtides_Figure5v2.PNG|thumb|right|600px|Figure 5. TAPtides prediction page.]]
The TAPS window for performing tidal harmonic predictions of water levels may be opened from the SMS interface by clicking on the Data menu and then selecting ''Tidal Predictions'' <nowiki>|</nowiki> ''Water Levels''. The window will display a list box in the upper right corner with the names of tidal constituent files created from previous Tidal Harmomic Analysis. As examples, two MATLAB data files (extension .mat) should appear from the Ballyheige and Chesapeake Bay analyses described in the previous section. Double click on either one to start.


After opening a tidal constants file, the file name and analysis date will be displayed in the data box below the Select button. The symbols of the constituents used in deriving this file can be viewed by clicking on <nowiki>’</nowiki>Tidal Constituents<nowiki>’</nowiki> in the menu bar above the GUI page (not shown in Fig. 4). Select the month and year of the predictions wanted along with the other options displayed including units, plot grid, Local Standard time (LST) or Local Daylight Time (LDT)<ref>NOTE: It is assumed that observed current data files will not use daylight saving time.</ref>. Pressing the large PREDICT button will then populate the calendar matrix at left with the days of the month and year selected. A daily, weekly or monthly plot of the predicted tidal current is displayed after the user presses the appropriate button.
After double clicking on a file, the file name and analysis date (year and Julian day starting) is displayed in the data box. Set the month and year of the required predictions along with the units desired (these units are independent of the units used in TAPtides analysis). Check boxes are available to turn on a plot grid and allow a change from Local Standard Time (LST) to Local Daylight Time (LDT) always assuming that LST was used during analysis. Pressing the large PREDICT button will then populate the calendar matrix at left with the days of the month and year selected. A daily, weekly or monthly plot of the predicted tide is displayed after pressing the appropriate button.
<br style="clear:both" />


===Printing to a file===
===Printing to a file===
Checking the <nowiki>’</nowiki>''enable print to file''<nowiki>’</nowiki> box below PREDICT allows the user to print a series of 12-minute current predictions to a text file for the month and year selected. If the <nowiki>’</nowiki>''year''<nowiki>’</nowiki> button is also checked, predictions are printed for the year selected using a 30-minute prediction interval.
The ''enable print to file'' check box below the ''PREDICT'' button allows the user to print 12-minute tidal height predictions to a text file for the month and year selected. If the ''year'' box is also checked, predictions are printed for the year selected using a 30-minute prediction interval. Excel calendar date and time is printed for each height value.
 
===Histogram (Percentiles)===
[[Image:TAPtides_Figure6.PNG|thumb|right|500px|Figure 6. TAPtides height-frequency histogram for Ballyheige, Ireland.]]
To display a histogram of predicted tidal heights as a percentage of total time, check the ''histogram'' box before pressing the ''PREDICT'' button. A cumulative curve will appear with percentile markings for the heights that are equaled or exceeded 20, 50 and 80 percent of the time for the month selected. If the ''year'' box is also checked, the percentages refer to total time for the year selected.


===Predicted speed distributions===
<br style="clear:both" />
To display a histogram of the flood and ebb current speed distributions, depress either the <nowiki>’</nowiki>''histogram1(percent)''<nowiki>’</nowiki> or <nowiki>’</nowiki>''histogram2(hours)''<nowiki>’</nowiki> radiobutton. The histogram distributions include the ''mean current'' value appearing in the <nowiki>’</nowiki>Mean Current<nowiki>’</nowiki> databox on the Analysis page at the time the tidal constants file was saved (prior to saving, the user could have entered another value, including zero, in this box). If either histogram is selected along with <nowiki>’</nowiki>print to file<nowiki>’</nowiki> (or <nowiki>’</nowiki>print to file<nowiki>’</nowiki> and <nowiki>’</nowiki>year<nowiki>’</nowiki>), a text file of the histogram values is printed in place of the serial current predictions.


Examples of predicted flood and ebb speed distributions in San Francisco Bay (NOAA PORTS station near Richmond, California) for 2008 are shown in Fig. 5. It is apparent in these graphs that higher current speeds favor the ebb over the flood phase at this station. This result is directly related to a strong diurnal inequality in the peak ebb currents at Richmond as illustrated in Fig. 6.
===LAT and HAT estimates===
If the tidal constants file selected does ''not'' contain a vertical datum offset (i.e., MSL-LAT=0.0), the histogram of predicted tidal heights will display the lowest astronomical tide (LAT) and the highest astronomical tide (HAT) for the month or year selected (Figure 6). Final estimates of LAT and HAT for use as reference datums can be found using the Analysis program (see Vertical Datums).


[[Image:CHETN_TAPcurrents_15Oct08_07.png|framed|Figure 5a. Flood and Ebb Predicted Current Speed Distributions for 2008 at Richmond, San Francisco Bay, CA (sc = surface current at Richmond).]]
===HAT estimate===
If the tidal constants file selected ''does'' contain a vertical datum offset (i.e., MSL-LAT<nowiki>></nowiki>0.0), the histogram of predicted tidal heights will reference heights above LAT and display the highest astronomical tide (HAT) for the month or year selected. Although generating most tidal height predictions relative to HAT would be confusing due to largely negative numbers, HAT is a good vertical reference for comparing storm tide peaks. HAT marks the extreme upper limit of the astronomical tide for a given time and place and its contour against the shore is often visibly marked (e.g., algal lines on rocks and piles). Normal tides will reach this contour in most, but not all years. And by using HAT as a reference, one can compare "extratidal" water levels between locations that have different tidal ranges.


[[Image:CHETN_TAPcurrents_15Oct08_08.png|framed|Figure 5b. Flood and Ebb Predicted Current Speed Distributions for 2008 at Richmond, San Francisco Bay, CA (sc = surface current at Richmond).]]
==Analyzing Storm Surge and Storm Tides==
[[Image:TAPtides_Figure7.PNG|thumb|right|600px|Figure 7. Storm tide and storm surge at Yorktown, VA, Tropical depression ERNESTO, 1-Sep-2006.]]
''Storm tides'' are water levels made higher by the superposing of astronomical tides with ''storm surge'', the transient change in water level resulting from the effects of a storm. In the United  States, the term <nowiki>’</nowiki>storm surge<nowiki>’</nowiki> is used most often in connection with hurricanes and tropical storms, although tropical depressions and extra tropical storms or <nowiki>’</nowiki>northeasters<nowiki>’</nowiki> produce damaging storm surge as well. TAPtides is uniquely suited for conducting post-storm investigations of storm surge – it readily performs the task of separating the storm surge from water level observations and shows the nature of its interaction with the astronomical tide to produce the resulting water level extremes. An example from a NOAA tide station at Yorktown, Virginia, is shown in Figure 7. It was created from a TAPtides 29-day analysis of Yorktown records following a visit by tropical depression ERNESTO on 1 September, 2006.


[[Image:CHETN_TAPcurrents_15Oct08_09.png|framed|Figure 6. Predicted Current Speed at Richmond, San Francisco Bay.]]
Figure 7 provides a good illustration of the importance of <nowiki>’</nowiki>timing<nowiki>’</nowiki> between the arrival of the storm surge peak and the stage of the astronomical tide. The peak storm surge occurred much closer to low tide than high tide at Yorktown on the morning of September 1. The storm surge occurred during'' tropic tides'' evidenced by a strong ''diurnal inequality'' in the daily highs (Figure 7). The tides are mixed, mainly semidiurnal in this area. Thus the risk of an exceptional high storm tide was by no means spread evenly over a 24-hr period given the possibility of the storm surge peak arriving at another time. Figure 7 demonstrates the utility of the MATLAB figure editor in changing features such as scaling and labeling of figure axes, figure legends, and line thickness
<br style="clear:both" />


==Additional Information==
== Additional Information==
Questions about this CHETN can be addressed Alex Sánchez at (601-634-2027), FAX (601-634-3433), or e-mail: [mailto: Alejandro.Sanchez@usace.army.mil  Alejandro.Sanchez@usace.army.mil].
Questions about this CHETN can be addressed Alex Sánchez at (601-634-2027), FAX (601-634-3433), or e-mail: [mailto: Alejandro.Sanchez@usace.army.mil  Alejandro.Sanchez@usace.army.mil]. This Technical Note should be referenced as follows:


==References==
==References==
Boon, J.D., 2004. ''Secrets of the Tide: Tide and Tidal Current analysis and Predictions, Storm surges and Sea Level Trends''. Horwood Publishing, Chichester, U.K. 212 pp. Reprinted 2007.
*Bloomfield, P. (2000). "Fourier Analysis of Time Series: An Introduction." John Wiley & Sons, New York, 258 pp.
 
*Boon, J. D. (2004, 2007). "Secrets of the Tide: Tide and Tidal Current analysis and Predictions, Storm surges and Sea Level Trends." Horwood Publishing, Chichester, U.K. 212 pp.
 
*Cartwright, D. E. (2000). "Tides: A scientific history." Cambridge University Press, 292 pp.
 
*Doodson, A. T., and Warburg, H. D. (1944). "Admiralty Manual of Tides." Admiralty Charts and Publications, London, England, 270 pp.
 
*Munk, W. H. and Cartwright, D. E. (1966). "Tidal Spectroscopy and Prediction." Phil. Trans. Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 259, No. 1105, pp. 533-581.


Cartwright, D.E., 2000. ''Tides: A scientific history''. Cambridge University Press, 292pp.
*Pugh, D. T. (2004). "Changing Sea Levels: Effects of Tides, Weather and Climate." Cambridge University Press, 265 pp.


Pugh, David T., 2004. ''Changing Sea Levels: Effects of Tides, Weather and Climate''. Cambridge University Press, 265 pp.
*Schureman, P. (1958). "Manual of Harmonic Analysis and Prediction of Tides." U.S. Dept of Commerce, Coast and Geodetic Survey. Special Publication No. 98, Washington, D.C., 317 pp.


----
----


----
[[Utilities | CMS Utilities]]
[[CMS#Utilities |CMS Utilities ]]

Latest revision as of 18:14, 22 October 2010

Tidal Analysis and Prediction of Tides: TAPtides

By John D. Boon and Alejandro Sanchez

Purpose

The Coastal Inlets Research Program Technical Wiki herein describes the desktop computer program TAPtides for the Tidal Analysis and Prediction of water levels. Designed to be easy to use, its Graphical User Interface (GUI) permits quick separation of a time series of water level measurements into its tidal and non-tidal components using a selective least squares harmonic reduction employing up to 35 tidal constituents. After saving the tidal constants for the constituents selected during analysis, the user can generate predictions of the astronomical tide, the water level that varies at known tidal frequencies attributable to gravitational interactions between the earth, moon, and sun.

Introduction

Many software packages are available today that allow tide predictions to be made in tidal waterways throughout the world. With few exceptions, these programs use tidal constants determined by governmental agencies and the casual user of this software is generally unaware of any of the details involved in the analysis, not least the breakdown of observed water level variation into its tidal and non-tidal parts.


In many cases, little information is available to users on the length, quality or age of the water level time series used to estimate tidal constants. Predictions for coastal waterways that have undergone significant hydrologic change (storms, dredging activity) may be subject to errors resulting from outdated measurements. The software presented here gives users the ability to make tidal harmonic predictions where suitable data are available for calculating the tidal harmonic constituents.


TAPtides is the ideal package to explore and develop preliminary or finalized tidal predictions from serial records spanning several weeks to several months. Although its operating features are intuitive and can be quickly grasped by users familiar with MS Windows® terminology, it is important to have a general understanding of the theory of tides before using TAPtides. Comprehensive references such as Cartwright (2000) and Pugh (2004) are highly recommended for this purpose, as is Boon (2004) for a practical introduction.

Installation

To run TAPtides the MATLAB Component Runtime (MCR) program must first be installed using the MCRInstaller provided with the application package. When installing SMS select the option to install TAPtides and TAPcurrents. After unzipping the package in a working directory, right-click the TAPtides program icon to create a shortcut and place it on your desktop. Run the application by double-clicking on the icon: This will create a new folder with the required MCR programs. TAPtides is programmed in the MATLAB® technical computing language, a product of The MathWorks, Inc. The present program is compatible personal computers with the MS Windows operating system (Windows XP).

Overview

The TAPtides menu has two options Tidal Analysis and Tidal Prediction. The last two buttons launch programs to conduct water level analysis (TIDAL ANALYSIS) and generate tide predictions respectively (CHOOSING TIDAL CONSTITUENTS, TIDAL PREDICTION). The analysis portion of the software accepts several file types (see INPUT FILES). The files used in this CHETN are automatically downloaded during the installation process and are located within the TAPtides folder which is located in the SMS directory. The tidal prediction portion of the software requires tidal constituents (amplitudes and phases of individual tidal components) from the tidal analysis program.

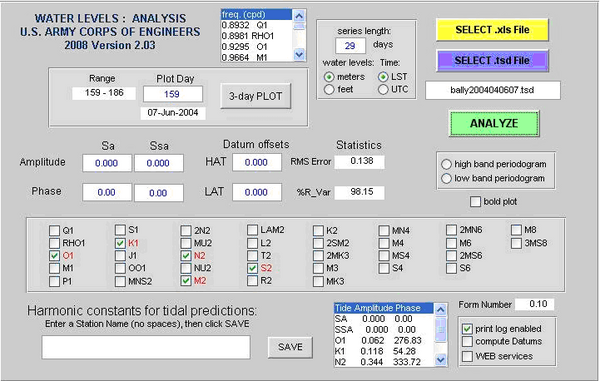
Tidal Analysis

Figure 1. TAPtides Analysis Page.

The method used by TAPtides to analyze a water level time series is commonly known as Harmonic Analysis, Method of Least Squares (HAMELS). It achieves a progressive reduction in variance (mean square deviation about the mean) by adding harmonic terms with specific astronomical frequencies to a general least squares model of the type used for multiple regression. It is not Fourier analysis, a procedure that employs only the Fourier frequencies. A brief description of HAMELS is given in Appendix B. For a complete description of the least squares harmonic analysis method employed here, the reader is referred to Boon (2004).


It is preferable to use the term water level analysis, rather than tide analysis, because the measured change in water level in coastal waterways varies at both tidal and non-tidal frequencies, including frequencies so low they appear as a static level or linear trend in short series. The objective of the analysis is to separate these components so that a tidal height prediction can be made with the component that is predictable – the water level that oscillates at tidal frequencies. To perform a water level harmonic analysis, click on the ’</nowki>Tidal Analysis<nowiki>’ button within the TAPtides window.


Clicking the Tidal Analysis button within the SMS menu Tools|Harmonic Analysis starts the GUI page that performs tide analysis (see Figure 1). It is recommended that the user click on the Disclaimer menu at the top of the window and read the disclaimer message before proceeding. Click the Program Help menu immediately to the left of the Disclaimer button to view information about input files, file analysis, selection of tidal constituents and other topics.


The analysis occurs in two steps:

  1. Settings and File Selection: Enter time series length (in days) and water level units (meters or feet). If the series length is left empty the total duration of the imported file will be used. If a number is entered that is larger than the input series length, a warning message will occur and the series length will be reduced automatically. Select a data file for analysis using the appropriate press button in the upper right corner of the page. Pressing a button will open a file browser displaying only files of the indicated type (MS Excel files with .xls extension or ascii text files with .tsd extension). Select a file and press the open button in the browser. If the print log enabled box is checked, a text file will be generated containing the parameters selected and other information from the analysis.
  2. Analysis: After the file is loaded, the message File ready for analysis will appear in the data box directly below the file selection buttons and the large Analyze button will turn green Pressing the ANALYZE button will start the analysis. The number of days in the file selected will be briefly displayed in the data box, followed by the date and time of the first record in the file and the file name. A graph will appear next showing the results of a least squares harmonic analysis fitting the five main tidal constituents, O1, K1, N2, M2 and S2, to the water level data (Figure 2). A list box at the bottom of the page displays the tidal constants (amplitude and phase) computed for all five constituents.


The check boxes in the center of the window indicate the tidal constituents available for harmonic analysis. Initially, only five major constituents are activated (shown in red text). The first five are always selected but the thirty others should be thought of as potential constituents that may be included in subsequent rounds of analysis. To include additional constituents, click on the check boxes for individual constituents and press the ANALYZE button. Selecting the proper constituents is explained in the next section.


For a relatively short time series of water levels (29 days to 58 days), there are limits to the number of constituents that can be used in a harmonic analysis. In general, the difficulty caused by short time series arises from the resolution of certain constituents that are close to others in frequency (consult the list box at the top of the Analysis page for a list of available constituents and their frequency). The main solar semidiurnal constituent S2, for example, has a frequency of exactly 2 cycles per mean solar day (cpd); the semidiurnal constituents T2 (1.9973 cpd), R2 (2.0027 cpd) and K2 (2.0055 cpd) are all very close to this frequency and can be difficult to resolve from a short series. The minimum series duration T necessary to fully resolve two tidal frequencies f1 and f2 is given by T =1/|f1-f2|, the synodic period. The synodic period for S2 and K2, for example, is 1/0.0055 or 181.8 days. Another important aspect to consider is the number of constituents chosen to model the tide. The user should start with the default constituents and choose additional constituents on the basis of their ability to reduce residual variance without violating the synodic period rule. Likely candidates will be found using the high band periodogram to examine the total distribution of variance (energy) with frequency. The periodogram feature is further explained below.

Three-day Plot

During analysis, the three-day plot feature in the gray frame on the upper left side of the TAPtides window may be used to closely examine three-day periods of the time series. Like the main plot which appears after pressing the ANALYZE button, the 3-day plot uses Julian days to display time (the corresponding calendar date is also displayed for convenience). The three-day plot of observed (red), predicted (blue) and residual (green) water level gives a wave-by-wave view showing how well the tidal harmonic model fits the data. A flat residual line indicates a good fit. If the predicted (blue) curve shows double peaks where the observed (red) curve only has single peaks, this may be an indication that too many tidal constituents are being used.


Another good reason to use the three-day plot is to investigate errors; e.g., dropped data points, vertical datum shift, or a shift to incorrect times. The least squares algorithm used in TAPtides is not affected by small data gaps (provided the time stamping remains correct). Although a short gap may be acceptable, the program will still issue a warning if the number of observations found is less than the number expected based on the series length specified and the calculated sampling rate based on the first two recorded sample times in the data series.

Additional Tools

Several tools are provided to assist the user in choosing constituents for inclusion in a harmonic model of the astronomical tide. Rather than relying on any single one of these tools, the user should use them in combination while keeping the series length in mind. Following a brief description of the available tools listed below, two examples of the recommended tidal analysis procedure are presented to illustrate their use.

Residual Periodogram

The residual periodogram is a line spectrum depicting the distribution of residual (measured minus predicted) energy at the Fourier frequencies. Fourier frequencies are multiples of the fundamental frequency 1/T and thus may not coincide with the tidal frequencies which, with the exception of the overtides (S4, S6, M4, M6, M8), are not multiples of any given frequency. However, with increasing series length Fourier frequencies become more numerous and bandwidth decreases, resulting in closer approximations to tidal frequencies. Using the data cursor in the MATLAB figure containing the high band periodogram (1-8 cpd), the user can determine the frequencies associated with the highest spectral peaks and look for the closest match to one of the tidal frequencies shown in the list box at the top of the analysis page, checking the appropriate box for the constituent indicated. At this point the user should consider each new constituent as only a candidate for inclusion in the tidal model, to be verified in subsequent analysis. Note that much of the residual variance displayed in any one periodogram may well be due to non-tidal meteorological forcing.


For convenience, both a high band periodogram (1 to 8 cpd) and a low band periodogram (0 to 3 cpd) are provided. The high band periodogram is well-suited for examining intertidal energy associated with transient events (e.g., storm surge). The low band feature can be used to examine subtidal oscillations that are usually associated with low frequency extratropical forcing. Subtidal energy (variance) in particular can be large compared to the tidal energy at certain locations. In those instances harmonic analysis will account for a low percentage of the total variance regardless of the number of tidal constituents used. Likewise the harmonic model of the tide cannot be deemed to have "failed" for this reason since it is designed to predict only the water level change occurring at tidal frequencies.

RMS Error and Percent Reduction in Variance

Two statistical parameters are provided near the center of the Analysis window to assist the user in evaluating the degree of success achieved by the model in representing the data. The RMS error, calculated as the square root of the mean square difference between observed and predicted water levels, is a measure of the expected error associated with an individual water level prediction. The Percent Reduction in Variance (%R_Var) is the percentage of the total variance in water level explained by the astronomical tide model. Ideally, inclusion in the model of any one constituent suggested by the periodogram should result in a noticeable decrease in RMS error combined with an increase in %R_Var. Again, if the data are taken from a region with strong meteorological forcing in relation to the tidal regime, it will not be possible to achieve either a high %R_Var or a low RMS error.

Constituent Amplitude and Phase Estimates

After conducting an analysis with a new tidal constituent added to the model, the user should check the amplitude found for that constituent in the list box at the bottom of the Analysis window. It should exceed at least one percent of the largest major constituent amplitude. More importantly for a short series, it should not cause another constituent at an adjacent frequency to change either its amplitude or phase by more than a few percent (K2 and S2 may be exceptions). When this occurs, it indicates that the harmonic model derived will yield erroneous future predictions even though the present fit to the observed water level data appears good in all other respects.

Tidal Form Number

This number indicates the relative dominance of semidiurnal and diurnal tides. It is calculated as F = (K1+O1)/(M2+S2) where the constituent names represent their respective amplitudes. The tides can be described as semidiurnal for F<0.25, mixed semidiurnal for 0.25>F>1.5, mixed diurnal for 1.5>F>3.0, and diurnal for F>3.0.

Analysis in Stages

To proceed with an analysis, the user should work in stages starting with the five major constituents (O1, K1, N2, M2, S2), as Stage I. After pressing the radiobutton to select the high band periodogram, proceed with the following steps:

  1. Using the data cursor, identify the peak frequencies shown in the residual periodogram and match them to the nearest tidal frequency shown in the list box. In most cases, the Fourier frequencies will not match the tidal frequencies exactly for the reasons previously given
  2. Check the boxes of constituent(s) selected above as candidates for Stage II. Constituents of different type classes (diurnal, semidiurnal, etc.) may be included in one stage but several constituents within the same class that are adjacent in frequency should not be included together.
  3. With the high band radiobutton remaining on, press ANALYZE to begin Stage II.
  4. Verify the constituent(s) selected as model candidates in the previous stage by confirming (1) peak elimination in the residual periodogram, (2) appropriate size for the resulting constituent amplitude as displayed in the lowermost list box, (3) decreased RMS error, increased %R_Var. Uncheck the constituent if it clearly fails any of these tests. Otherwise, the new stage will be marked by a periodogram showing new residual peaks at a lower energy level. To amplify the remaining peaks at each new stage, the y-coordinate scale expands as the energy level drops.
  5. Select constituent candidates as before for Stage III. Continue this process until all constituents that can be successfully matched to a residual peak frequency are found and included in the astronomical tide model.

When analyzing a short series (58 days or less), look for signs of poor resolution between neighboring constituents on the frequency scale. This usually takes the form of a large change in amplitude and phase for such constituents when analyzed jointly versus separately. For tides of small range especially, selecting a constituent that is very close in frequency to one of the major constituents in a short series should be avoided; e.g., T2 (1.9973 cpd) and R2 (2.0027 cpd) adjacent to S2 (2.0000 cpd).

Seasonal Constituents

The Analysis window contains four data boxes on the left side with zero values entered in blue. They allow the user to manually enter an amplitude and phase for the solar annual (Sa) and solar semiannual (Ssa) tide constituents (optional). These numbers are available for most primary tide stations in the United States and can be applied at nearby stations as well. Otherwise, several years of observations are required to determine Sa and Ssa, the so-called seasonal tides.

Vertical Datums

TAPtides analysis adopts the vertical reference of the user’s data in all of its calculations. TAPtides predictions are normally made relative to mean sea level (MSL) but provide the option of generating predictions relative to Lowest Astronomical Tide (LAT), a tidal datum commonly used outside the United States. Unlike other tidal datums that require a lengthy tabulation of observed high and low water heights, LAT is derived as the lowest predicted tide over a 19-year lunar node cycle and thus depends entirely on the accepted tidal constants for the station involved. A similar datum, Highest Astronomical Tide (HAT), is derived as the highest predicted tide over the same interval. Both datums are computed as offsets from MSL. The numbers appearing in the datum offset boxes on the analysis page are saved with the tidal constants used in making tidal predictions (see TIDE PREDICTIONS). If the blue numbers that initially appear are left at zero, tidal predictions will be generated relative to MSL; otherwise, by entering a negative number to indicate its offset below MSL, predictions will be made relative to LAT. To obtain offsets, check the compute Datums box in the lower right corner of the page before clicking on the ANALYZE button for the final analysis. When this box is checked the program internally performs 19 years of predictions to find and display the HAT and LAT offsets relative to MSL. Caution: Use a water level record of at least 180 days duration to obtain tidal constants for reliable datum determinations.

Printing to file

After checking the enable print to file check box, pressing the ANALYZE button will save a listing of the observed, predicted and residual water levels in a text file (*.txt) with the same name as the input Excel file.

Saving Results

Once, a satisfactory tidal analysis is obtained, the results may be saved in a binary MATLAB data file. The variables stored in this file may be examined using the MATLAB load command by entering a file name (without the .mat extension) in the data entry box in the lower left corner and pressing SAVE.

Input Files

The TAPtides analysis tool accepts two file types containing input water level time series. The first is a Microsoft Excel Workbook (*.xls) or TAP Excel File. The web services utility, described in Appendix A, allows users to directly download water level data from active NOAA stations and output the data in TAP Microsoft Excel Worksheet files. The second file format allowed in TAP is the SMS Time Series Data file (*.tsd) or tsd file. The Time Series Data files are useful file format because they can easily be imported into SMS for viewing, model forcing and comparison with model results. Other file formats such as the SMS XY Series files and generic ASCII files may be converted to TAP Excel files or tsd files using the utility Filter1D also provided and optional installation software in SMS 10.1+.

Time Series Data File

The second file format which is supported in the analysis page of TAPtides is the Time Series Data file (*.tsd). This file is supported in SMS versions 10.1+. The ASCII file consists of two header lines followed by data columns separated by spaced or tabs. The first line contains the identifier TIMESERIES. The second line contains 5 elements. The first element is the name of the time series within apostrophes. The second element specifies the curve type and may be one of: "Unassigned", "Vel. & Mag.", or "Vel. Components". The third element is an integer specifying the number of input columns including the time stamp (column 1). The forth element is the length of the input time series. The fifth element is a reference date and time of the first data point. The date and time are specified as "mm/dd/yyy HH:MM:SS" where mm is the month, dd is the day, HH is the hour, MM is the minute, and SS is the seconds. The input time series does not need to have a regular time interval.

TIME_SERIES
"CRCR2007" "Unassigned" 2 1535 "03/01/2007 00:00:00"
0.00 0.227
1800.00 0.198
3600.00 0.168
5400.00 0.137
7200.00 0.104
9000.00 0.070
10800.00 0.036


TAP Microsoft Excel Worksheet.

These files consist of an array of water level data entered on the first worksheet of a Microsoft Excel workbook (*.xls). The first line of the worksheet is reserved as a header line usually used to describe data columns. Two separate formats are available for data entry in the subsequent rows:

  A. Col. 1 - Record number, station number or Julian day (not used in calculations)
    Col. 2 - Date in Excel month-day-year-time format (3/14/01 13:30)
    Col. 3 – Water level in feet or meters (Columns > 3 must be empty)
  B. Col. 1 - Record number, station number or Julian day (not used in calculations)
    Col. 2 - Date in Excel month-day-year format (3/14/01)
    Col. 3 - Local Standard Time in Excel 24-hour time format (13:30)
    Col. 4 – Water level in meters or feet

A set of non-numeric column labels may be inserted as the first row of either array. Note that a 4th column is not allowed when using format A.

Additional metadata such as instrument type, location etc. should be stored in separate worksheets.

Pre-set constituent selection

To avoid having to check multiple constituent symbol boxes each time the user repeats a tidal analysis, a worksheet named tidecn may be added to the Excel file after the first worksheet containing the water level data. This worksheet must contain the list of symbols for TAPtides’ 37 tidal constituents (including Sa and Ssa) in the first column of the tidecn worksheet in order of increasing frequency moving downward. Enter the amplitude and phase of Sa and Ssa, if known, in the second and third columns; otherwise enter zeros. For the remaining constituents, enter ’1’ or ’0’ in the second column to indicate symbols to be automatically checked or unchecked once the file has been loaded; enter a zero in the third column. An example of the tidecn worksheet can be found in Excel file SWPT20070101R6m.xls.

Tidal datums

To display the position of vertical datums on monthly (30-day) water level plots, enter datum elevations in a new worksheet named datums, placing this tab in any position after the first worksheet in the Excel workbook with one of the formats in Table 1.

Table 1. Formats allows for datums worksheet.

a. U.S. format   b. Non-U.S. format
Datum Elev.(ft)   Datum Elev.(m)
plotmax 6.00   plotmax 3.00
HAT 3.53   HAT 2.47
MHHW 2.76   MSL 0.00
MSL 1.35   STND 0.00
MLLW 0.00   LAT -2.51
LAT -0.69   plotmin -3.00
plotmin -2.00  

STND is the station datum or the zero point of the measurement scale in use (in feet or meters). If MSL in relation to the station datum is unknown, it should be set to zero.

After a few seconds, the main TAPtides window will appear with four program choices: coopsVhr, coopsR6m, Tide Analysis, and Tide Prediction. The first two buttons allow the user to quickly download verified hourly heights (coopsVhr) or raw six-minute heights (coopsR6m) from the National Oceanographic and Atmospheric Administration (NOAA) network of active tide stations.

Examples

Two example data sets are presented below. Both contain water levels record in meters, the default setting for TAPtides analysis. The edit box appearing above the units selection will initially appear blank. After the input file has been selected and read, the number of days available in the file will be displayed. The user may change this setting to a lesser number but not less than 14 days.

Ballyheige, Ireland

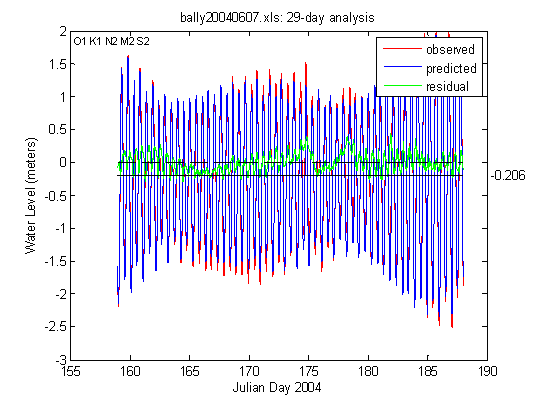
Figure 2. Analyzed water level at Ballyheige (series mean level: -0.206m).

The first example is from Ballyheige, a town at the entrance to the Shannon River in western Ireland (bally20040607.xls). To get a feel for the use of the features described above, the reader can run a 30-day analysis of input file bally20040607.xls which contains water levels sampled at 5-minute intervals at Ballyheige (Data supplied courtesy of the Irish Geological Survey, Dublin, Ireland). After selecting this file the data box will display the number of days in the file followed by the date and time of the first record and the file name. After it has turned green, press the ANALYZE button to begin the analysis.


A window graph will appear displaying the observed water level (red), the astronomic tide (blue) and the residual (green) or difference between observed and predicted.. A pop-up message should also appear indicating a data gap within the file (8,340 records found, 8,353 expected). Whenever this message is seen, the cause should be sought by examining the input file. The gap in this example is too small to be seen in the 30-day plot. Using the 3-day plot feature, the gap can be clearly seen mid-morning on Julian day 173 (21-Jun-2004) at the point where the red curve abruptly shifts to the right by one hour. This is a time shift rather than a simple data gap and it means that all of the times past this point must be reduced by one hour. To skip the correction and proceed with the analysis, open the Excel file and move the worksheet labeled ’Fixed_file’ to the first position in the example workbook.


Figure 3. High Band Periodogram.

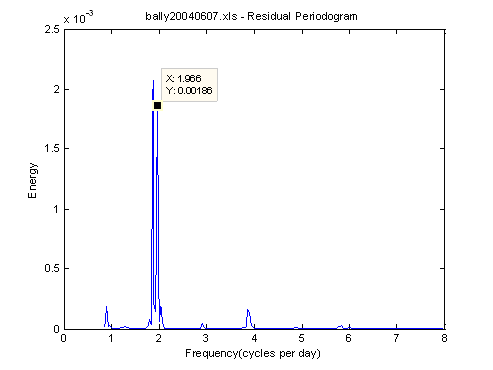
After loading and reading the fixed file, run the analysis again with the high band periodogram turned on. A Fourier periodogram will appear displaying two prominent peaks at adjacent frequencies. Using the data cursor, click on the left peak. An x-axis reading of approximately 1.862 cpd should be visible. Clicking on the peak to the right, 1.966 cpd should appear (Figure 3). The first frequency falls midway between constituents 2N2 and MU2; The second midway between LAM2 and L2. For the first stage of analysis with the five major constituents, the RMS error will read ±0.138 m and the percent reduction in variance (%R_Var) should read 98.15.


Tidal harmonic analysis is a form of multivariate analysis. To monitor the variables (constituent amplitude and phase) employed in a step-wise (stage) analysis the user should consider entering the amplitude and phase of all the constituents involved at each stage on a separate worksheet. One has already been entered in the bally20040607.xls file (tab labeled Stage Analysis). Selecting all four constituents 2N2, MU2, LAM2, and L2 produces a large change in the tidal amplitudes indicating that this choice is unacceptable for a series of this length. Choosing the one constituent near each peak with the greatest amplitude will produce a better result. After selecting MU2 and LAM2, the RMS error is reduced to ±0.109 m and %R_Var is increased to 98.80 percent.


In the next stage of the analysis, the first dominant peak suggests constituents Q1 and RHO1 and the second one matches the quarter-diurnal constituent, M4. Referring again to the Stage Analysis worksheet, RHO1 and M4 emerge as the most reasonable choices, reducing the RMS error to ±0.105 m and increasing %R_Var to 98.88 percent. In the final stage, MNS2, K2, M3, MN4, MS4 and M6 are added, reducing RMS error to ±0.100 m and increasing %R_Var to 98.98 percent. Noting the change in amplitude and phase for S2 at this stage may be surprising to some users, but in this instance it is clearly linked to relatively large amplitude in the luni-solar semidiurnal constituent, K2. K2 is often one of the major constituents in regions where the tide type is fully semidiurnal and the range is more than two meters (the mean range at Ballyheige is approximately three meters). Normally the K2 spectral peak is not pronounced in a short series because of its proximity to S2 which is included at the outset as one of the major constituents.


During the course of the above four stages, the peak energy shown in the periodogram falls by two orders of magnitude – from about 2 x 10-3 to about 3 x 10-5 m2/cpd. At this point we may enter a name and save the 15 constituents selected in a tidal constants file (e.g., Ballyheige_MSL to indicate that no offset from MSL was used).

Chesapeake Bay, USA

The second example is from a water level station at the Chesapeake Bay entrance (cbbt20021101.xls) courtesy of the U.S. National Oceanic and Atmospheric Administration (NOAA). This example also involves a 30-day analysis of water levels. The file named cbbt20021101.xls was obtained from the NOAA Tides & Currents web site and includes hourly water level data for 30 days beginning November 1, 2002. As with the previous example, a stage analysis for this file can be found on a separate worksheet in the Excel workbook. Tidal type here is mixed, mainly semidiurnal.


Analysis in stages yields 13 constituents for this file (Q1, O1, M1, K1, J1, OO1, MNS2, MU2, N2, M2, L2, S2 and K2) but, unlike example 1, the resulting model accounts for only 71.33 percent of the variance in water level. The reason why can be clearly seen in the residual curve for the window plot of the 30-day series. During this particular month, a subtidal oscillation was present at the bay entrance whose amplitude at times exceeded the amplitude of the astronomical tide. Switching to the low band periodogram, a peak frequency is shown at 0.2069 cpd (period = 4.83 days). Although a longer analysis would improve estimates of harmonic constituents such as S2 and K2 in the astronomical tide model, the increase in %R_Var would be small compared to the subtidal energy.

Special Features

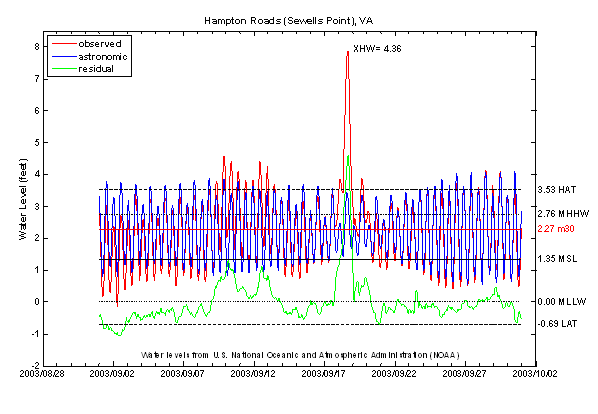
Figure 4. Water level history for Hampton Roads, VA, September, 2003.

Providing tidal constants for water level predictions is one application of TAPtides. It is also useful for informative graphs displaying monthly water level histories at active monitoring stations. Water levels in near real time are now routinely displayed at NOAA PORTS stations on the web. These contain plots typically covering the past three days showing whether observed water levels are trending above or below predicted levels. A monthly plot can add value to this product by displaying monthly and weekly variations in tidal range in relation to non-tidal events such as a transient storm surge appearing in the residual curve. An example of a monthly plot is shown in Figure 4, at the Hamptons Roads, VA water level station during Hurricane Isabel. The observed water levels are shown in red, the fitted astronomical tides in blue, and the residuals containing the storm surge component in green. These figures are useful in understanding the extreme storm tides that result from the superposition of storm surge and astronomical tides.


Tidal Predictions

Figure 5. TAPtides prediction page.

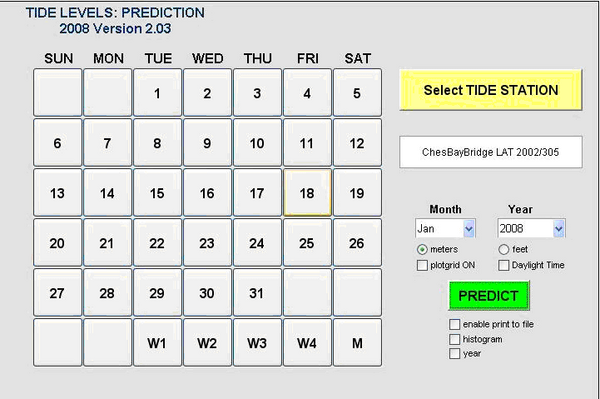
The TAPS window for performing tidal harmonic predictions of water levels may be opened from the SMS interface by clicking on the Data menu and then selecting Tidal Predictions | Water Levels. The window will display a list box in the upper right corner with the names of tidal constituent files created from previous Tidal Harmomic Analysis. As examples, two MATLAB data files (extension .mat) should appear from the Ballyheige and Chesapeake Bay analyses described in the previous section. Double click on either one to start.

After double clicking on a file, the file name and analysis date (year and Julian day starting) is displayed in the data box. Set the month and year of the required predictions along with the units desired (these units are independent of the units used in TAPtides analysis). Check boxes are available to turn on a plot grid and allow a change from Local Standard Time (LST) to Local Daylight Time (LDT) always assuming that LST was used during analysis. Pressing the large PREDICT button will then populate the calendar matrix at left with the days of the month and year selected. A daily, weekly or monthly plot of the predicted tide is displayed after pressing the appropriate button.

Printing to a file

The enable print to file check box below the PREDICT button allows the user to print 12-minute tidal height predictions to a text file for the month and year selected. If the year box is also checked, predictions are printed for the year selected using a 30-minute prediction interval. Excel calendar date and time is printed for each height value.

Histogram (Percentiles)

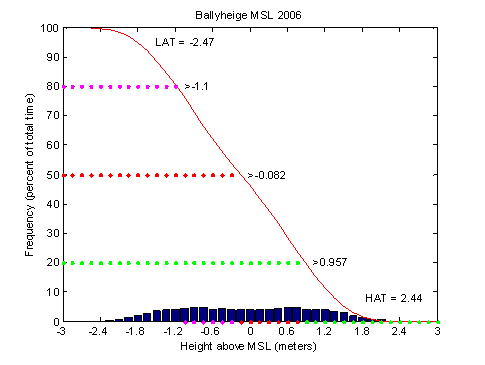
Figure 6. TAPtides height-frequency histogram for Ballyheige, Ireland.

To display a histogram of predicted tidal heights as a percentage of total time, check the histogram box before pressing the PREDICT button. A cumulative curve will appear with percentile markings for the heights that are equaled or exceeded 20, 50 and 80 percent of the time for the month selected. If the year box is also checked, the percentages refer to total time for the year selected.


LAT and HAT estimates

If the tidal constants file selected does not contain a vertical datum offset (i.e., MSL-LAT=0.0), the histogram of predicted tidal heights will display the lowest astronomical tide (LAT) and the highest astronomical tide (HAT) for the month or year selected (Figure 6). Final estimates of LAT and HAT for use as reference datums can be found using the Analysis program (see Vertical Datums).

HAT estimate

If the tidal constants file selected does contain a vertical datum offset (i.e., MSL-LAT>0.0), the histogram of predicted tidal heights will reference heights above LAT and display the highest astronomical tide (HAT) for the month or year selected. Although generating most tidal height predictions relative to HAT would be confusing due to largely negative numbers, HAT is a good vertical reference for comparing storm tide peaks. HAT marks the extreme upper limit of the astronomical tide for a given time and place and its contour against the shore is often visibly marked (e.g., algal lines on rocks and piles). Normal tides will reach this contour in most, but not all years. And by using HAT as a reference, one can compare "extratidal" water levels between locations that have different tidal ranges.

Analyzing Storm Surge and Storm Tides

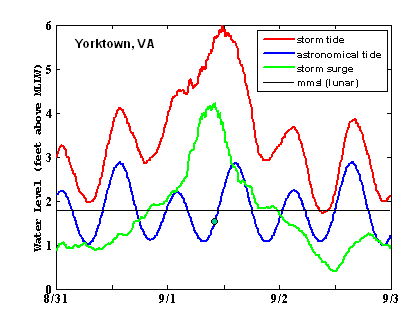
Figure 7. Storm tide and storm surge at Yorktown, VA, Tropical depression ERNESTO, 1-Sep-2006.

Storm tides are water levels made higher by the superposing of astronomical tides with storm surge, the transient change in water level resulting from the effects of a storm. In the United States, the term ’storm surge’ is used most often in connection with hurricanes and tropical storms, although tropical depressions and extra tropical storms or ’northeasters’ produce damaging storm surge as well. TAPtides is uniquely suited for conducting post-storm investigations of storm surge – it readily performs the task of separating the storm surge from water level observations and shows the nature of its interaction with the astronomical tide to produce the resulting water level extremes. An example from a NOAA tide station at Yorktown, Virginia, is shown in Figure 7. It was created from a TAPtides 29-day analysis of Yorktown records following a visit by tropical depression ERNESTO on 1 September, 2006.

Figure 7 provides a good illustration of the importance of ’timing’ between the arrival of the storm surge peak and the stage of the astronomical tide. The peak storm surge occurred much closer to low tide than high tide at Yorktown on the morning of September 1. The storm surge occurred during tropic tides evidenced by a strong diurnal inequality in the daily highs (Figure 7). The tides are mixed, mainly semidiurnal in this area. Thus the risk of an exceptional high storm tide was by no means spread evenly over a 24-hr period given the possibility of the storm surge peak arriving at another time. Figure 7 demonstrates the utility of the MATLAB figure editor in changing features such as scaling and labeling of figure axes, figure legends, and line thickness

Additional Information

Questions about this CHETN can be addressed Alex Sánchez at (601-634-2027), FAX (601-634-3433), or e-mail: [mailto: Alejandro.Sanchez@usace.army.mil Alejandro.Sanchez@usace.army.mil]. This Technical Note should be referenced as follows:

References

  • Bloomfield, P. (2000). "Fourier Analysis of Time Series: An Introduction." John Wiley & Sons, New York, 258 pp.
  • Boon, J. D. (2004, 2007). "Secrets of the Tide: Tide and Tidal Current analysis and Predictions, Storm surges and Sea Level Trends." Horwood Publishing, Chichester, U.K. 212 pp.
  • Cartwright, D. E. (2000). "Tides: A scientific history." Cambridge University Press, 292 pp.
  • Doodson, A. T., and Warburg, H. D. (1944). "Admiralty Manual of Tides." Admiralty Charts and Publications, London, England, 270 pp.
  • Munk, W. H. and Cartwright, D. E. (1966). "Tidal Spectroscopy and Prediction." Phil. Trans. Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 259, No. 1105, pp. 533-581.
  • Pugh, D. T. (2004). "Changing Sea Levels: Effects of Tides, Weather and Climate." Cambridge University Press, 265 pp.
  • Schureman, P. (1958). "Manual of Harmonic Analysis and Prediction of Tides." U.S. Dept of Commerce, Coast and Geodetic Survey. Special Publication No. 98, Washington, D.C., 317 pp.

CMS Utilities

Retrieved from "https://cirpwiki.info/index.php?title=TAPtides&oldid=3767"