Inlet Geomorph Bibliography: Difference between revisions

From CIRPwiki
Jump to navigation Jump to search
No edit summary
No edit summary
 
(11 intermediate revisions by the same user not shown)
Line 6: Line 6:
A literature review of several topic papers on inlet geomorphic parameterization and classification are given in the below annotated bibliography.  The Papers are categorized by subject matter: 1) Classification, 2) Processes, 3) Relationships, and 4) Structural Response.
A literature review of several topic papers on inlet geomorphic parameterization and classification are given in the below annotated bibliography.  The Papers are categorized by subject matter: 1) Classification, 2) Processes, 3) Relationships, and 4) Structural Response.


<br  style="clear:both" />


'''1) Classification'''
[[Image:Inlet_geomorph_fig3_Hayes.png|thumb|right|400px]]


:* Shoreline classification based upon tide range
'''1) [[Inlet_Geomorph_Bibliography-Classification | Classification]]'''
:** Microtidal coasts (T.R. 0-2 meters) (wave dominated coasts)
:** Mesotidal coasts (T.R. 2-4 meters)
:** Macrotidal coasts (T.R. > 4 meters) (tide dominated coasts)


:* Variation in inlet planform morphology can be caused by
:*Shoreline classification based upon tide range
:** time variation of wave energy
:**Microtidal coasts (T.R. 0-2 meters) (wave dominated coasts)
:** time variation of tidal energy (prism),
:**Mesotidal coasts (T.R. 2-4 meters)
:** space variation of tidal energy (prism), and
:**Macrotidal coasts (T.R. > 4 meters) (tide dominated coasts)
:** evolution of ebb-tidal deltas and adjacent shorelines.


'''2) Processes'''
:*Variation in inlet planform morphology can be caused by
:**time variation of wave energy
:**time variation of tidal energy (prism),
:**space variation of tidal energy (prism), and
:**evolution of ebb-tidal deltas and adjacent shorelines.


:* Euilibrium properties of coastal structures exist over all time scales and can be used to simplify models and relationships.
<br  style="clear:both" />
:*   North Carolina and northern South Carolina are classified as microtidal wave dominated, southern South Carolina and Georgia as mesotidal tide-dominated, and the northeast coast of Florida as microtidal wave dominated.
 
:* Physical and geological parameters impact tidal inlet variability.
'''2) [[Inlet_Geomorph_Bibliography-Processes | Processes]]'''
:* The tide dominated inlets are characterized by large ebb-tidal deltas extending far out from shore, well-defined deep main channels and inlet throats, and an absence of inner shoals, except where fresh water inflow induces stratification and landward bottom sediment transport.
 
:* Sediment is bypassed at inlets through:  
:*Equilibrium properties of coastal structures exist over all time scales and can be used to simplify models and relationships.
:*North Carolina and northern South Carolina are classified as microtidal wave dominated, southern South Carolina and Georgia as mesotidal tide-dominated, and the northeast coast of Florida as microtidal wave dominated.
:*Physical and geological parameters impact tidal inlet variability.
:*The tide dominated inlets are characterized by large ebb-tidal deltas extending far out from shore, well-defined deep main channels and inlet throats, and an absence of inner shoals, except where fresh water inflow induces stratification and landward bottom sediment transport.
:*Sediment is bypassed at inlets through:  
:** Stable inlet processes
:** Stable inlet processes
:**Ebb-tidal delta breaching Inlet migration and spit breaching
:**Ebb-tidal delta breaching Inlet migration and spit breaching
Line 35: Line 40:
:**Jettied inlet bypassing
:**Jettied inlet bypassing
:**Outer channel shifting at jettied inlets
:**Outer channel shifting at jettied inlets
:*           Normal  0            false  false  false    EN-US  X-NONE  X-NONE                                                                                                                                                                                                                                                                                                                                                                    Degree of sheltering at an inlet and the back bay environment can effect flood or ebb dominance and create a tidal velocity asymmetry at the inlet. This can, in turn, effect the morphology of the inlet.
:*Degree of sheltering at an inlet and the back bay environment can effect flood or ebb dominance and create a tidal velocity asymmetry at the inlet. This can, in turn, effect the morphology of the inlet.
:*           Normal  0            false  false  false    EN-US  X-NONE  X-NONE                                                                                                                                                                                                                                                                                                                                                                    The direction of tidal forcing was the main parameter governing orientation of the main inlet channel and ebb delta.
:*The direction of tidal forcing was the main parameter governing orientation of the main inlet channel and ebb delta.
 
 
 
 
 
 
--------------
 
* Watlon and Adam's Tidal Prism to Ebb Shoal Volume Relationship
* ___
 
 
 
'''Shigemura, T., 1981.  Tidal prism – throat width relationships of the bays of Japan.  Shore & Beach, Volume 49, No. 3, pp. 34-39.'''
Shigemura studied 231 natural bays, to which no artificial works had been added, along the four major coasts of Japan. He defined the throat area as the cross-sectional area at the narrowest section, or throat, of a bay entrance. Previously (Shigemura, 1980) he developed a relationship between the throat area and the tidal prism of the form A=CPn. In this paper he examines ten (10) external variables through a correlation analysis to determine which exerts the most significant influence on throat width. Based on this analysis, Shigemura arrives at basic correlation relationships, separated by coast, of the form Wt=CPn. Because these initial relationships do not account for external variables such as littoral drift, geological or geometrical features Shigemura refines the relationships based on seven “geometrical parameters.” In order to evaluate the significance of the parameters, he defines a reliability parameter of the regression equation and performs a correlation analysis between the reliability parameter and the geometric parameters. He found that, of all the Wt-P equations, the parameter rwl (the ratio of the throat width to the shore length of the bay) had a high correlation with the reliability parameter and, based on this information, uses the rwl parameter further refine the correlations by classifying the bays into four groups. Additionally, the paper includes a discussion of equations other researchers have developed and provides a discussion of values for the C and n variables throughout the stages of refinement.
 
'''Hansen, M. and Knowles, S. Ebb-Tidal Delta Response to Jetty Construction at Three South Carolina Inlets, Lecture Notes on Coastal and Estuarine Studies, Vol. 29. D.G. Aubrey, L. Weishar (Eds.), Hydrodynamics and Sediment Dynamics of Tidal Inlets, Springer-Verlag, New York, Inc. 1988.'''
Hansen and Knowles examine three inlets; Charleston Harbor, Murrells and Little River Inlet in South Carolina. These inlets are within the transitional zone, between wave and tide dominated, as they have a tidal range of 1.5 meters, which identifies them as microtidal based on Davies (1964) classification system. All three inlets have rubblemound jetties with parallel ends and weir structures included in their design. The following identifying information was provided about the jetty dimensions.
{|
| Name || NE Jetty Extent (m) ||| SE Jetty Extent (m) |||| Jetty Tips (m)
|-
| Charleston Harbor || 4,700 ||| 5,800 |||| 884
|-
| Murrells Inlet || 1,053 ||| 1,011 |||| 198
|-
| Little River Inlet || 1,001 ||| 1,167 |||| 305
|}
 
The paper discusses the way in which construction of the jetties impacted each of the inlets. At Charleston Harbor Entrance the jetties dissected the ebb tidal shoal and diverted the main ebb flow seaward. Geomorphology remained essentially the same as prior to construction. The swash platform migrated seaward. At Murrells Inlet implementation of the jetties created a landward migration of the swash bars. Bar migration and welding of the shoal south of the jetties occurred within 4 years. A small lagoon was formed downdrift of the south jetty and a new ebb delta began forming seaward of the constructed jetties. Less than 5 years of data was available for Little River Inlet but the data indicated swash bar migration with lagoon formation, similar to the changes seen at Murrells Inlet.
 
The paper indicates that jetty construction at Murrells Inlet and Little River Inlet showed a rapid response, in comparison to Charleston Harbor. The response at the smaller inlets was similar to the response seen in the situation of ebb delta breaching. Confinement of the channel by the jetties created an effect of wave dominance of the ebb deltas in all three cases. Hansen and Knowles identify that at the smaller inlets the channel confinement and shoal migration has, in the time period analyzed, eliminated the typical morphological expressions of ebb deltas.
 
'''Walton, T.L., and Adams, W.D., 1976.  Capacity of inlet outer bars to store sand.  Proceedings, 1976 Coastal Engineering Conference, ASCE, pp. 1919–1937.'''
Walton and Adams investigated the equilibrium storage volume of sand in the outer bar/shoal of newly cut inlets. Inlets were classified into highly exposed, moderately exposed and mildly exposed to offshore wave action based on the H2T2 (wave height)2 * (wave period)2 parameter. The paper considers the inlet as a sediment sink to the adjacent shorelines and utilizes the equilibrium shoal volume in their calculations as the point at which the erosional influence to the adjacent shorelines is diminished. Walton and Adams utilized the “no-inlet contour method” of Dean and Walton (1973) to calculate ebb shoal volumes for 44 inlets in assumed equilibrium within the United States. They developed a relationship of the form V=aPb and used liner regression to determine the value for b for inlets separated by exposure and for all inlets together. Walton and Adams also determined that the ebb shoal volume and the inlet channel cross-sectional area relate to one another in the form A=a’Ab’.
 
Walton and Adams identified that in areas of high wave activity there appears to be a well-defined limiting relationship to the amount stored in the offshore bar as a function of tidal prism. They noted that the volume of sand in an inlets outer bar is strongly correlated to tidal prism and cross sectional inlet throat area. They found that more sand is stored in the outer bar of a low energy coast than is stored in the outer bar of a high energy coast.
 
The paper also included references to a number of tidal prism and inlet cross-section values and identified that future work in this area should take into consideration longshore energy and size distribution of littoral material and examine inner bay storage.
 
'''Pope, J. 1991. Ebb Delta and Shoreline Response to Inlet Stabilization, Examples from the Southeast Atlantic Coast. Proceedings, 1991 Coastal Zone, National Oceanic and Atmospheric Administration, pp. 643-654.'''
This paper studies four stabilized natural inlets along an ebb-tide dominated barrier island and the coastal and offshore response to jetty construction. Pope reviewed a combination of historic bathymetric change information, shoreline movement data, geomorphic assessments, wave refraction studies and sediment budgets in order to evaluate the impacts of entrance channel jetties on sediment supply, ebb delta modification and inshore erosion rates. The inlets examined are located on beach ridge barrier islands in an area with high tide ranges and low wave energies where, generally, inlets are formed and maintained by tidal currents and not closed by wave-induced longshore sediment transport. The four inlets examined were: Little River Inlet (NC/SC), Charleston Harbor Entrance (SC), Murrells Inlet (SC), and St. Mary’s Entrance (GA/FL). Murrells Inlet and Little River Inlet have been monitored since construction and have one kilometer long jetties. In comparison the inlets of St. Mary’s and Charleston Harbor are larger with jetties 5 kilometers and 6 kilometers long, respectively.  The paper provides details about each inlet and system including histories and details of the studies performed. Based on these observations, Pope developed a conceptual model of inlet evolution in response to stabilization. She concludes that, at these inlets, there is initial thalweg channelization and fillet trapping followed by a fairly rapid collapse of the natural ebb-delta lobe ad a steepening of the ebb delta platform. Included in this paper are figures of long term and short term response to jetty construction. It is noted that there appears to be a direct correlation between inlet size and response time of inlet morphology changes.
 
'''Gibeaut, J.C., and Davis, R.A., 1993. Statistical geomorphic classification of ebb-tidal deltas along the west-central Florida coast. Journal of Coastal Research SI(18), 165-184.'''
This paper describes morphologic type of tidal inlets on the west central Florida barrier island chain. Gibeaut and Davis utilized aerial photographs to analyze the ebb tidal delta planform shape for 9 inlets (Longboat Pass, Redfish Pass, Dunedin Pass, Captiva, New Pass, Big Sarasota Pass, Stump Pass, Midnight Pass and Gasparilla Pass). They utilized a number of historical non rectified vertical aerial photographs for each inlet and digitized the swash platform, the shoreline landward of the swash platform, and the outline of the main ebb channel thalweg. In the paper probability functions are utilized to describe the seaward outline of the ebb-delta terminal lobe for the inlets examined. The sources of error in the digitization process are described. A cluster analysis of morphological parameters (ebb delta area, left shoreline offset, right shoreline offset, channel position and channel angle) was performed. The cluster analysis showed inlet configurations to be a continuum with characteristic inlet types identifiable at the end points in the continuum. The groupings that were defined in the cluster analysis were separated by tidal classifications (wave dominated, mixed energy, mixed energy with large shoreline offset and large asymmetry and tide dominated). A discussion of controls on inlet form and size is included within this paper along with a discussion of how natural and anthropogenic changes (i.e., changes in prism, dredging, tide, waves, etc.) cause changes in inlet morphology. They conclude by identifying four factors which cause variation in an inlet planform morphology: 1) time variation of wave energy, (2) time variation of tidal energy (prism), (3) space variation of tidal energy (prism), and (4) evolution of ebb-tidal deltas and adjacent shorelines.
 
'''Jarrett, J.T., 1976.  Tidal prism – inlet area relationships. GITI Report 3, U.S. Army Engineer Waterways Experiment Station, Vicksburg MS. 55 pp.'''
In this paper Jarrett discussed the works of LeConte (1905), O’Brien (1931), Nayak (1969 and 1971) and Johnson (1972). Jarrett obtained data from 108 inlets on all coasts of the United States and discusses the sources and methods of obtaining this information. Jarrett classified the inlets into three main categories (1) all inlets, (2) unjettied or single jettied inlets, and (3) inlets with jetties. He also classified them by coast. Jarrett identified a relationship between inlet area and tidal prism of the form A=CPn and presents the data in table and graph form within the paper. He also discussed the differences in the relationships between the different groups. This paper is also valuable in that it contains referenced tables of tidal prism, cross sectional area, hydraulic radius, and tidal current data for the 108 inlets in his study.
 
'''FitzGerald, D.M., and FitzGerald, S.A., 1977.  Factors influencing tidal inlet throat geometry. Proceedings, Coastal Sediments 77 Conference, ASCE, pp. 563-581.'''
FitzGerald and FitzGerald define and assess the parameters that affect tidal inlet throat geometry. Initially, the work of previous researchers in the area of inlet throat geometry is discussed. FitzGerald and FitzGerald define the inlet throat as the part of the channel which is the narrowest and deepest and has the maximum hydraulic radius. The inlet throat has the minimum cross-sectional area and maximum current velocities. FitzGerald and FitzGerald discuss the size, depth, channel symmetry and sedimentological control of the inlet throat. In this paper FitzGerald and FitzGerald investigated eight central South Carolina inlets (mesotidal inlets) to determine factors which influence the symmetry of the inlet throat. They discuss that symmetry is a product of (1) meandering of the channel thalweg, (2) inlet shoreline configuration, and (3) dominant longshore transport direction. Temporal variations in throat cross-section are developed. They discuss the variations in throat cross-sectional area and short-term changes at Price Inlet, SC and the long-term changes of Stono Breach, Dewees and Capers Inlets, SC. A table of historical changes in throat geometry is presented. They develop the relationship of cross-sectional area versus tidal range for Price Inlet of the form Y=947+119X. The paper discusses the channel response over a complete tidal cycle at Pierce Inlet in order to evaluate if the inlet throat cross-sectional area responds quickly to changing tidal conditions.
 
'''Gaudiano, D.J., and Kana, T.W., 2001.  Delta bypassing in South Carolina tidal inlets: geomorphic variables and empirical predictions for nine mesotidal inlets. Journal of Coastal Research, 17(3), pp. 280-291.'''
Nine South Carolina (mixed energy coast) tidal inlets (2 stabilized and 7 not stabilized) were examined to determine the relationship between the volume of sand in the ebb-delta and the individual bypassing shoals, the time interval between bypassing events and the tidal prism. A conceptual model of shoal bypassing was validated. The paper includes a literature review of ebb breaching. Aerial photographs over a 53-58 year time period were digitized and examined to identify bypassing events. The inlets included in the evaluation were: Midway, Pawleys, North, Pierce, Capers, Dewees, Breach, Stono and Captain Sams Inlets. The shoal volumes were determined from the aerial photographs by measuring the plan area of the shoals and then multiplying by an estimated thickness of three meters. This method assumed vertical sides on the shoal so, a scaling factor was introduced to account for the missing volume. Following this analysis, the average annual contribution from the delta to the adjacent beaches was computed from which the local annual sediment transport was calculated. Gaudiano and Kana also included the results of field studies conducted to measure inlet throat cross sections and tidal prisms for seven of the nine inlets. A linear relationship between the average shoal bypassing event interval (I) and the tidal prism (Tp) was found of the form I=0.046Tp+4.56. They were able to identify that larger inlets undergo shoal bypassing events less frequently than smaller inlets and that the variable I is related to the longshore sediment transport rate. Gaudiano and Kana developed a relationship of the form S=6.42Tp+113.4 which describes the relationship between the average bypassing shoal volume and the tidal prism. They described qualitatively a point in the quantity of sediment supply to the system which will induce bypassing.
 
Additionally, Gaudiano and Kana plotted the shoal volume/tidal prism data obtained from the seven inlets they examined onto the Walton and Adams (1976) best fit line. Gaudiano and Kana determined that the seven South Carolina Inlets all plotted above the Walton and Adams best-fit line. They postulated that a greater influence of the tides in South Carolina may be the cause of this difference.
 
Gaudiano and Kana identified that the shoal bypassing mechanisms identified by FitzGerald (1978) were present with the South Carolina inlets. They identified inlet migration and spit breaching, periodic landward migration of swash bars and ebb-tidal delta breaching. The paper describes the breaching process at each of the inlets examined.
 
'''Hayes, M.O., 1979.  Barrier island morphology as a function of tidal and wave regime. In: Barrier Islands form the Gulf of St. Lawrence to the Gulf of Mexico, S.P. Leatherman (Ed.). Academic Press, NY, pp. 1-27.'''
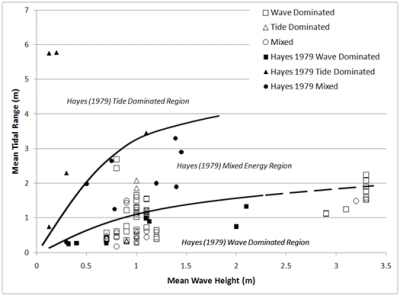
In this paper, Hayes identifies two factors, wave energy and tidal current energy control geomorphology of depositional coasts and that both of these are related to tide range (T.R.). Hayes discusses Davies (1964) who classified shorelines based on tide range:
• Microtidal coasts (T.R. 0-2 meters) (wave dominated coasts)
• Mesotidal coasts (T.R. 2-4 meters)
• Macrotidal coasts (T.R. > 4 meters) (tide dominated coasts)
 
Hayes provides inlets which are examples of each case and provides the associated references but focuses on coasts with medium wave energy (Mean Significant Wave Height (MSH) = 60-150 cm). Additionally, Hayes provides the geomorphologic differences of the mesotidal and microtidal cases in table form and discussion within the table.
 
Additionally, Hayes classified and plotted 21 barrier island shorelines based upon mean tidal range and mean wave height and into five morphological types: wave dominated, mixed-energy wave dominant, mixed-energy tide dominant, tide-dominated (high) and tide-dominated (low). Hayes concludes that, for coasts with medium wave energy, the tidal classification of Davies (1964) needed refinement and that the boundary between microtidal and mesotidal is thought to be too high. Hayes added the classification of low-mesotidal for areas where the tide rages are between 1-2 meters for coasts of medium wave energy.
 
In this paper, Hayes also discusses the relationship between shoreline morphology and shoreline embayments and the effects of climate on barrier morphology.
 
 
'''Powell, M.A., Thieke, R.J., and Mehta, A.J. 2006. Morphodynamic Relationships for ebb and flood delta volumes at Florida’s tidal entrances. Ocean Dynamics, Volume 56, pp. 295-307.'''
This paper reviews relationships between cross sectional area, ebb delta volume, flood delta volume and tidal prism based on data from 67 sandy entrances in Florida. This paper contains a list of these 67 Atlantic and Gulf Coast inlets which include data of Latitude, Longitude, tidal range, wave energy, flux, grain size, depth, flow area, tidal prism, and ebb and flood volumes. The paper includes discussion of and multiple references to previous work. Powell, Thieke and Mehta plotted prism versus throat area for all inlets examined and found a best-fit equation of the form Ac=6.25x10-5P1.0. They further discussed ebb delta volume and tidal prism noting that the ebb delta volume is determined by tidal currents and waves. A review of the literature is included as part of the discussion on ebb delta volume and tidal prism. Additionally, the authors applied the previously defined equations to the data from the 67 Florida inlets studied. Further the authors identify relationships between flood delta volume and tidal prism and discuss the initial volume growth of the flood delta and perform a best-fit analysis as was done in the ebb delta case. At the terminus of the paper the authors include a case which identifies the effect of the closure of a storm induced breach near Matanzas Inlet, FL.
 
_____________________________________________________________________________________
 
'''Fitzgerald, D.M., and Nummedal, D, 1983. Response characteristics of an ebb-dominated tidal inlet channel.  Journal of Sedimentary Petrology, 53(3), pp. 833-845.'''
This paper details the study of changes in the main channel of Price Inlet, SC on timescales ranging from hours to years. Price Inlet is a barrier island inlet located on the mixed-energy South Carolina coast north of Charleston Harbor. The field work that was carried out for this research occurred between 1974 and 1977. Fitzgerald and Nummedal discuss water storage and tidal stage in the Price Inlet drainage basin including a discussion of water surface area in the back barrier and throat cross-section cross-sectional area over the tidal cycle. Migration and morphological changes of the tidal channel were also monitored at three cross-sections along the inlet channel. Cross-sectional area was measured on a bi-monthly basis measured at slack water.
 
It was concluded that the inlet cross-section is highly sensitive to changes in tidal range because of the relationship between tidal range and potential sediment transport. The paper also includes a discussion of channel change during one tidal cycle as it relates to sediment transport. The calculated magnitude of potential inlet sediment transport is high enough at Price Inlet to suggest that significant changes in inlet hydraulic geometry can be expected during a single tidal cycle. This hypothesis is tested over a single cycle on July 29, 1977 through monitoring of the throat cross-section and inlet flow parameters. Throat current velocities and cross-sectional areas were measured each hour and changes of the areas are discussed in the paper. Longer-term changes in the morphology of Price Inlet was found to be controlled by the growth of the ebb-tidal delta shoals and growth of the channel-margin linear bars. The bars reduce transport into the inlet and thus results in a larger channel equilibrium cross-sectional area.
 
'''Riedel, H.P., and Gourlay, M.R. 1980, Inlets/Estuaries Discharging Into Sheltered Waters. Coastal Engineering, pp. 2550-2564.'''
The study was motivated by the design of a new international airport in Australia. During this design process an existing stable creek (Serpentine Creek) was reclaimed and flood waters were diverted into an artificial inlet (Moreton Bay). In order to design this reclamation and diversion, Riedel and Gourlay investigated characteristics of inlets and estuaries discharging into sheltered waters.
 
This area of Australia has a mild wave climate with low wave heights and small waver periods. Also, this area has low littoral drift rates. Although a literature review of the relationships previously derived for tidal inlets on open coasts are included in this paper, Riedel and Gourlay acknowledge that these relationships are not likely to apply in this case.
 
A literature search of Australian studies was performed for this research and a short discussion of this literature is included in this paper. Field studies were undertaken to obtain relationships. Tide, current and limited hydrographic data was obtained for four inlets and their estuaries in South East Queensland (Beelbi Creek in Hervey Bay, Tingalpa, Serpentine and Burpengary creeks in Moreton Bay). These were selected because of their similarity to the proposed artificial inlet (including sediment similarity). The data obtained consisted of: Tide records, tidal velocities, hydrographic surveys to define cross-sectional areas and tidal prisms.
 
Riedel and Gourlay identified that there are differences between the stability characteristics of small inlets discharging into sheltered waters and large systems connected through an exposed shoreline but that the difference is purely in turns of scale. For a given cross-sectional area of the inlet entrance the tidal prism for the exposed coast inlets is approximately 2 to 3 times those of sheltered inlets. Sheltered inlets have smaller littoral drift rates and cross sectional areas of sheltered entrances are larger than for exposed inlets for a given prism and velocities will be lower. Riedel and Gourlay also included a discussion of the relationship between cross sectional area and tidal prism for estuaries.
 
'''Tomlinson. 1991. Processes of Sediment Transport and Ebb Tidal Delta Development at A Jettied Inlet.'''
The paper begins with a short discussion of sediment transport processes due to anthropogenic modifications to inlets. The paper focuses on the development of the ebb tidal delta following the extension of jetties at the Tweed River entrance in northern New South Wales, Australia. A database of coastal processes of this area (Tomlinson and Foster, 1986) formed the basis of this study. The paper provides background information on the study area including history of the structuring of the inlet and river. A model of the ebb delta morphology was developed beginning in 1873 prior to the 1902 jetty construction and prior to the 1962 extensions.
 
The impact on the coastal processes due to the extension of the jetties is discussed as is a detailed description of the ebb delta development. Introduction of the jetties caused the shoal to be established further offshore than previously and with a more symmetrical shape.
 
The authors were able to determine the temporal delta volume beginning in 1978 from bathymetric surveys. Discussion of the changes in sediment deposition and a prediction of the ultimate size of the ebb delta (using Walton and Adams, 1976) is included. The paper concludes with the evaluation that the delta development transitioned from deposition dominated by tidal flow to a state of dynamic equilibrium between the tidal flow and the wave-induced transport across the delta.
 
'''Mehta, A.J.; Dombrowski, M.R., and Devine, P.T., 1996.  Role of waves in inlet ebb delta growth and some research needs related to site selection for delta mining.  Journal of Coastal Research, SI 23, pp. 212-136.'''
A motive of this paper was to obtain an understanding of the processes occurring at the ebb delta in terms of deposition in order to assess how these processes and effect ebb delta mining. In this paper, the role of waves in modulating the growth of ebb tidal deltas has been examined for four Florida east coast entrances (Jupiter Inlet, South Lake Worth Inlet, Boca Raton Inlet and Bakers Haulover Inlet). Volumes of the ebb deltas were determined using the Dean and Walton method (1973).
 
A model is presented in this paper to explain delta growth based upon an analysis of bottom shear stress from current and wave influence (Tb) and the critical stress for scour (Tcr) where, when Tb<< Tcr deposition occurs until they are approximately equal. At this point there is no further deposition and there is an equilibrium water depth above the delta and the delta reaches an equilibrium volume. The influence of wave energy would increase the delta volume (increased wave energy) or decrease the delta volume (decreased wave energy) and the shoal would move away from this equilibrium volume. Details regarding these conditions and relating hydraulic and morphodynamic parameters to the delta area are then explained within the paper.
 
The four Florida entrances examined in this paper have mostly littoral transport components with minimal riverine influences. They are examined by the authors to assess the effects of waves compared with tidal currents as the deltas transition from the no inlet condition to equilibrium. The author’s utilized the Obrien ratio of wave power to tidal prism power and plotted growth rate curves over time based on the high and low values of this ration. The curves were then compared to the measured ebb volumes. The ebb delta volume growth curves grow monotonically, reaching an asymptotic condition (indicating a dynamic equilibrium of the ebb shoal). The equilibrium delta volume condition was also examined in this paper.
 
The focus of the paper then turned to examples of delta mining with examples from US entrances and a discussion of considerations of in mining site selection criteria.
 
'''ertel, G.F., 1988.  Processes of sediment exchange between tidal inlets, ebb deltas and barrier islands.  Lecture notes on Coastal and Estuarine Studies, Volume 29, Springer-Verlag New York, Inc. NY, pp. 297-318'''
The introduction of this paper includes a brief discussion of literature as it related to prism area relationships and bypassing of sediment and inlet stability. Hydraulics and sedimentary processes at inlets are then discussed, initially in the absence of sediment transport outside of the channel itself. The paper then turns to a discussion of the processes occurring at the ebb tidal delta. Formation of the delta and the differences between the ebb and flood flow processes. Following is a discussion on equilibrium delta budgets the amount of material stored in an ebb delta. Oertel then introduces the concept that material may originate from the inlet gorge or from the adjacent littoral drift. Focus was placed on the amount of material available from the inlet gorge.
 
In this study, nine tide dominated inlets were examined. Their ebb delta volumes were determined through the Dean and Walton method (1975) and tidal prisms were either measured or found in literature. Based upon this data two equations relating bar volume and prism (mean and spring prisms) were determined. The plots were compared to the Walton and Adams (1976) data for tidal prism. This comparison is discussed within the paper. Diversion of the inlet jet by longshore current is discussed along with the sediment transport implication this diversion created on the inlet channels (i.e. inlet migration). Georgia and North Carolina inlets were used as examples.
 
Four types of deltas (with varying degrees of longshore versus onshore currents) are discussed with regard to bypassing and channel migration. Illustrations of tidal inlets are included which identify channel orientations caused by different magnitudes of inlet migration and sediment bypassing. 
 
Cobb Island in Virginia is presented as a case study in island sediment budgets and illustrations are included identifying cases where barrier island shorelines change but their budgets remain balanced i.e., stability by rollover, stability by spit growth, stability by migration, and stability with constant shoreline position (complete bypassing).
 
'''FitzGerald, D.M., 1996.  Geomorphic variability and morphologic sedimentologic controls on tidal inlets.  Journal of Coastal Research, SI 23, pp.47-71.'''
Geomorphic variability at tidal inlets is discussed in this paper. FitzGerald defines a tidal inlet as an opening in the shoreline through which water penetrates land, connecting the ocean and bays, lagoons, marsh and tidal creek systems. He describes that the main channel of the tidal inlet is maintained by tidal currents, distinguishing a tidal inlet from open embayments or rock bound passages where there is little or no mobilized sediment.
 
FitzGerald describes a history of morphologic models for inlet shoreline alignment, ebb tidal shoal processes, hydrographic regime and temporal changes at inlets and includes graphical depictions of the models described. FitzGerald then summarizes geomorphic and sedimentologic controls on tidal inlets. These include: sediment supply, basin geometry, regional stratography, occurrence of bedrock, riverine discharge and sea level changes. He also describes secondary controls with interaction of two or more of the factors previously mentioned.
 
Ebb tidal and inlet throat morphology is discussed as is the relationship to waves and tidal prism and the effects of deltas on the inlet shoreline. A table of tidal ranges and wave heights and prisms of mixed energy (tide dominated) shorelines of the world is included within this paper. Relationships between tidal prism and throat are and literature on the topic is discussed in this paper as is the dynamic relationship between tidal prism and inlet throat cross-sectional area.
 
Case studies of backbarrier processes are discusses in the East Friesian Islands, central Couth Carolina and in Chatham Harbor, Cape Cod. Additionally, a case study at the Saco River estuary and Kennebec River estuary in Maine are included in a discussion of estuary/inlet interaction and salinity effects. Finally, research needs are discussed.
 
'''FitzGerald, D.M., 1982.  Sediment bypassing at mixed energy tidal inlets. Proceedings 18th Coastal Engineering Conference, ASCE Press, pp. 1094-1118.'''
FitzGerald examines inlet sediment bypassing through stable inlet processes and ebb delta breaching at six mixed energy (tide-dominated) coasts at non-structured tidal inlets. As an introduction, the work by Bruun and Gerritsen (1959) is discussed whereby the type of bypassing processes at an inlet can be determined by the ratio between longshore sediment transport and maximum discharge at the inlet under spring tidal conditions.
 
FitzGerald describes the new landward sediment transport due to landward directed currents over the ebb shoals terminal lobe which retard ebb currents and enhance flood currents. Additionally, the model of bar migration up the shore face with associated stacking of the swash bars is shown. Ebb tidal delta breaching caused by a dominant direction of longshore sediment transport is discussed. This, in turn, results in downdrift migration of the main ebb channel, eventually breaching of the shoal to form a new, more hydraulically efficient channel and bar migration onshore.
 
Examples of bypassing from five regions are discussed: Maine coast, central South Carolina, East Friesian Islands along the West German North Sea, the southern New Jersey coast, the Virginia Coast and the Gulf of Alaska Cooper River Delta.
 
The location of the bar welding is discussed as it influences erosional and depositional patterns along the barrier island. The bar welding location is affected by the inlet size, wave versus tide dominance and channel orientation. These mechanisms are discussed.
 
'''Seabergh, William C. Long-Term Coastal Inlet Channel Area Stability.'''
Seabergh applies the concept of equilibrium area of tidal inlets (LeConte, 1905 and O’Brien 1931 and 1969) to inlets that are not in equilibrium i.e. inlets with bays that do not fill completely but still exhibit fairly consistent channel flow over many years. Seabergh discusses work by others on inlet equilibrium which do not require complete bay infilling for maintenance of stable channels.
 
The Kulegan (1967) “K” repletion coefficient is introduced to define the percentage that the bay fills. A number of examples from US inlets with low K values are presented in table form. This is discussed in concert with the Escoffier (1940, 1977) equilibrium curve which requires complete bay filling, whereby the Escoffier analysis of tidal inlet cross-sectional area equilibrium for cases with existing low K values indicates that equilibrium area will be much larger than the existing area. However, the low K inlets may not expand their entrance cross-sectional area in the absence of anthropogenic changes (dredging, structure implementation, etc.).  


'''Marino, J.N., and Mehta, A.J., 1987.  Inlet ebb shoals related to coastal parameters.  Proceedings, 1987 Coastal Sediments Conference, American Society of Civil Engineers, pp. 1608-1623.'''
In this paper, the evolution of ebb tidal shoals is introduced through a discussion of a time history of St. Augustine Inlet (opened in 1941) including jetty construction and dredging history. Marino and Mehta examined eighteen inlets on Florida’s east coast were examined, relating their ebb shoal volume to spring tidal prism, inlet cross-sectional area, inlet width, inlet depth and sprig tidal amplitude. Ebb shoal volumes were determined through the Dean and Walton method (1973). Published values, or estimates based on literature, were used for the values of cross-sectional area, width, depth, prism and wave data. A dimensional analysis was utilized to determine functional relationships which may relate to ebb shoal volume. The paper examined the ebb shoal volume vs spring tidal prism relationship of Walton and Adams (1976) to determine which parameters explain the scatter in the Walton and Adams data within the same energy range. The discussion also examines the influence of bed shear stress, current shear stress, wave shear stress and channel depth.


Conclusions of the paper contain estimates of the total amount of material found within the 18 examined ebb shoals and identifies a general trend of decreasing ebb shoal volume from north to south along the East coast of Florida. Marino ad Mehta conclude that the ebb shoal volume appear to be a function of spring tidal prism, inlet area, tidal amplitude and the ratio of inlet width to depth (which arises as a result of the effect of wave induced sediment transport at varying depths over the ebb shoal).
<br  style="clear:both" />


'''Vincent, Corson and Gingrich, 1991. Stability of selected United States Tidal Inlets.'''
'''3) [[Inlet_Geomorph_Bibliography-Relationships | Relationships]]'''
The motivation of this study was continuation of the USACE funded initiative of promoting safe navigation through tidal entrances. Vincent, Corson and Gingrich studied 51 US tidal inlets through a series of historical aerial photographs to examine tidal inlet stability. The paper includes a discussion of previous research on this topic. Vincent, Corson and Gingrich identify four types of inlet instability: geographic, rotational, meandering and channel stretching. They introduce hydraulic parameters (width and length) and positional parameters (migration) related to inlet stability. Stability indices are then derived. The paper discusses stability analysis based on a photographic analysis performed by the authors of the minimum channel width, channel traces and the channels seaward end point. The authors review inlet variability over time to determine the variability of the 51 inlets in the channel width, length, channel position and throat. Relationships among time variant characteristics are added in table form for all combinations of channel width, length, channel position and throat in combinations of time variant properties (random variation, cyclic short period variation, cyclic long period variation and trend variation). Vincent, Corson and Gingrich discuss stability of the 51 inlets examined utilizing relative hydraulic and relative geographic stability parameters. Regional patterns and trends identified through examination of the 51 inlets are described. Appendices include aerial photograph dates, a listing of stability indices (position orientation, width and length) throughout time for the inlets studied, and plots of temporal variations in channel position and orientation, channel width and traces for all inlets studied.


'''Fitzgerald, D.M., Kraus, N.C., and Hands, E.B. 2001. Natural mechanisms of sediment bypassing at tidal inlets. ERDC/CHL CHETN-IV-30, U.S. Army Engineer Research and Development Center, Vicksburg, MS.'''
:*The two main principles in bypassing of sand by natural action; bypassing on an offshore bar and bypassing by tidal flow action or a combination of these two methods.
In this paper, Fitzgerald, Kraus, and Hands present sediment bypassing at natural and modified inlets. They identify bypassing through examination of sequences of aerial photographs and bathymetric maps. The mechanisms identified include:
:*The ratio of Mmean/Qmax=r (magnitude of littoral drift) and quantity of flow through the inlet can assist in the identification of these mechanisms. If the ratio is high r>200-300, bar bypassing is predominant. A lower ratio, r<10-20 indicates tidal flow bypassing.
:*A relationship between inlet area and tidal prism of the form A=CPn exists
:*Symmetry is a product of (1) meandering of the channel thalweg, (2) inlet shoreline configuration, and (3) dominant longshore transport direction.
:*A method called the “no-inlet contour method” has been introduced to calculate ebb shoal volumes
:*A relationship is introduced between ebb shoal volume and tidal prism of the form V=aP<sup>b</sup>
:*The ebb shoal volume appear to be a function of spring tidal prism, inlet area, tidal amplitude and the ratio of inlet width to depth (which arises as a result of the effect of wave induced sediment transport at varying depths over the ebb shoal).  
:*Delta growth is explained based upon an analysis of bottom shear stress from current and wave influence (Tb) and the critical stress for scour (Tcr) where, when Tb<< Tcr deposition occurs until they are approximately equal. At this point there is no further deposition and there is an equilibrium water depth above the delta and the delta reaches an equilibrium volume. The influence of wave energy would increase the delta volume (increased wave energy) or decrease the delta volume (decreased wave energy) and the shoal would move away from this equilibrium volume.
:*A linear relationship between the average shoal bypassing event interval (I) and the tidal prism (Tp) was found of the form I=0.046Tp+4.56. It was found that larger inlets undergo shoal bypassing events less frequently than smaller inlets and that the variable I is related to the longshore sediment transport rate.
:*A relationship of the form S=6.42Tp+113.4 has been used to describe the relationship between the average bypassing shoal volume (S) and the tidal prism (P).
:*Four types of inlet instability have been identified: geographic, rotational, meandering and channel stretching.
:*Inlet stability may be thought about in terms of (1) hydraulic parameters (width and length) and (2) positional parameters (migration).
:*Relationships between tidal prism and the planview shape of the ebb shoal have been developed.


• Stable inlet processes – This is the case of stable inlets with non-migrating throats and stable main ebb channel position through the ebb delta. At these inlets bypassing occurs through formation of large bar complexes which migrate and attach to the downdrift shoreline.
• Ebb-tidal delta breaching – In this case, the throat is stable and the main ebb channel cyclically migrates downdrift.
• Inlet migration and spit breaching – In this case, throat constriction is caused by longshore transport and bar breaching reestablishes a new, ore hydraulically efficient channel. This type of movement can be identified by the presence of an updrift spit and elongation of the tidal channel. The new inlet channel may be opened due to differences in the tidal phase and tidal range between the ocean and the back barrier. The new inlet may form during a storm. The old (migrated) inlet is increasing less hydraulically efficient and closes.
• Outer channel shifting – This type of bypassing is limited to the seaward end of the main ebb channel and involves smaller sediment volumes than the ebb-tidal delta breaching model. The outer channel is deflected downdrift while the main channel remains fixed. As the outer channel becomes more and more deflected, it becomes hydraulically inefficient.
• Spit platform breaching – This type of bypassing occurs at migrating inlets where asymmetric channel configurations form due to the influence of the updrift barrier spit. The new channel is breached through the spit platform under this mechanism. This is analgious to flow through a river meander bend. In this form, secondary channels may be created.
• Bypassing at wave dominated inlets - Wave dominated inlets form arcuate ebb shoals close to shore and transport of sediment occurs continuously along the periphery of the delta aver the shallow distal portion (especially at high tide).
• Jetty-weir bypassing - Jetty-weir bypassing occurs at inlets with one or two weirs and no settling basin. Transport into the weirs is most active during storms. The sediment in the weir can be transported seaward by ebb currents. This type of bypassing occurs most at inlets when ebb currents are strong enough to transport sands out of the channel.
• Jettied inlet bypassing – Seidement bypassing at jettied inlets occurs when excess sediment accumulated on the updrift beach. The amount of sediment accumulation and bypassing is dependant upon the jetty length, inlet size, channel depth, total current strength, and ebb shoal morphology.  In this case, the jetties funnel ebb discharge and displaces the ebb shoal further offshore thus reducing the effects of waves retarding the formation of bar complexes. Transport along the outer bar by wave action occurs primarially during storms.
• Outer channel shifting at jettied inlets. In this form of bypassing deflection of the outer channel and shoal breaching, to produce a more hydraulically efficient channel. Sediment from the relic shoal is transported onshore due to wave action.


These types of bypassing mechanisms are discussed in this paper along with the volume of sediment transported through each of these mechanisms and bypassing frequency.
<br  style="clear:both" />


'''Hubbard, D.K., Barwis, J.H., and Nummedal, D., 1977. Sediment Transport in Four South Carolina Inlets.  Proceedings, Coastal Sediments 1977. pp. 582-601.'''
'''4) [[Inlet_Geomorph_Bibliography-Structural Responses | Structural Responses]]'''
This paper presents hydrographic studies at four South Carolina inlets (Fripp, Stono, Murrells, and Little River) to investigate sediment transport patterns through the inlet throat and across adjacent shoals. This work builds upon research on the variability in inlet types. Also included is a discussion of a model for ebb tidal delta circulation. As part of this research, current velocities and tidal lengths were measured hourly for 26 hours at each of the four inlets. During the studies the researchers noted the importance of wave induced sediment transport. A more detailed study was begun at Murrells inlet. Wave observations were taken over an 8 day period. Suspended sediment samples were collected over four days to determine sediment transport rates. Swash bar migration rates were also measured to estimate bedload transport. Tidal current processes in the main channel, swash platforms, swash bars and channel margin bars of the four inlets are discussed in this paper along with the sediment transport processes associated with each case. The authors observed that degree of marsh development controls the ebb and flood dominance at the inlet and that the relative elevation of the water at the maximum flood and ebb flows effects channel flow through the inlet. The features of swash platforms and swash bars are described in this paper. Swash bar surfaces are dominated by landward flow. This dominance can result in time velocity asymmetry from topographic influences and wave input. Each influences are discussed. The authors also describe how wave processes effect sediment transport in tidal inlets. At Murrels inlet, the waves break in much shallower water, relative to wave heights) on flood than on ebb due to the effects of the currents. This process effects sediment transport on the bar. Previously established sediment transport rates from CIRC (1973) were compared to the measured data collected as part of this research. It was concluded that the theoretical relationships, based on fluvial or flume data may have questionable application in the tidal environment.


'''Carr, E.E., and Kraus, N.C., 2001. Morphologic asymmetries at entrances to tidal inlets. Report Number ERDC/CHL CHETN-IV-33, U.S. Army Engineer Research and Development Center, Vicksburg, MS.'''
:*The introduction of jetties have caused ebb shoals to extend further offshore than previously with a more symmetrical shape.
This paper discusses characteristics of selected symmetries in morphological forms at tidal entrances and begins with a listing of potential applications for the research. The sediment bypassing processes and associated morphologic features are identified and discussed. The concept of ebb shoal symmetry/asymmetry is introduced as are the three asymmetry indicators that have been measured at the tidal inlets considered in this study. The asymmetry indicator measurements (WA1, WA2, and L) are utilized to describe the degree of asymmetry in the ebb shoal. WA1 is defined as the distance to the updrift point where the ebb shoal complex attaches to the shoreline. WA2 is defined as the distance where the ebb shoal complex attaches to the shoreline. L is defined as the distance of the offshore extent of the ebb shoal. The measurements of the ebb shoal asymmetry indicators were taken from various aerial photographs and NOS nautical charts. Examples of ebb shoal symmetry and asymmetry from specific inlets are included.  
:*A methodology for determining a net drift direction at a project site was introduced that includes:
:**Office examination of data
:**Field visit with aerial over flight
:**Discussions with specialists
:**Review of wave records
:**Collection of supplemental field data
:*The Inlet reservoir Model (IRM), calculates sediment transport rates and volume change of identified morphologic features and bypassing rates for an inlet.
:*The IRM can be used as an inlet management tool with a general methodology for simulating the evolution of different features and assessing consequences of interruption in sediment transport across inlets.
:*When the combined shear stress (τb) is smaller than the critical shear stress (τcr) deposition will occur until the shear stresses are balanced τb=τcr , when equilibrium is reached.  


Relationships of the form WA1,WA2=aPb, where P is tidal prism, were developed through linear regression analysis. The data was separated by number of jetties at each inlet to determine the coefficients of each case. The seaward extent of the ebb shoal, L, was similarly related to tidal prism, P.
________________________________________________________________________


Finally, temporal changes in the asymmetry indicators are discussed using a case study of St. Augustine Inlet, FL based upon changes from the 1950’s to 1999. A brief discussion on asymmetries of inlet channels is also included.


'''Nummedal, D., Oertel, G.F., Hubbard, D.K., and Hine, A.C., 1977.  Tidal inlet variability- Cape Hatteras to Cape Canaveral.  Proceedings, 1977 Coastal Sediments Conference, American Society of Civil Engineers, pp. 543-562.'''
*[[Inlet_Database | Inlet Database]] Page
A discussion of tidal range along the east coast study area begins this paper. It classifies North Carolina and northern South Carolina as microtidal wave dominated, southern South Carolina and Georgia as mesotidal tide-dominated, and the northeast coast of Florida as microtidal wave dominated. The paper builds on studies of tidal range to include wave energy, inner shelf slope and hydrologic properties of the inlets associated lagoon. Physical parameters such as wave action and tidal current are discusses within the study area. The authors then turn to a discussion of geological parameters. These include total lagoon area, open water area, percent open water area to total maximum throat depth, ebb tidal delta area, inner shoal area, maximum offshore distance of ebb tidal delta, distance to the 18 foot offshore depth contour and inner shelf slope. These values are provided for representative inlets in North Carolina, South Carolina, Georgia and Florida. Physical parameters are compared and discussed for the inlets in each of the states examined. The authors preformed a qualitative analysis of sediment transport mechanisms in a zone of wave and current interactions to improve understanding of tidal inlet process-response characteristics. A figure of states vs physical and geological parameters is included with the discussion.


'''Bruun, P., 1995. The development of downdrift erosion.  Journal of Coastal Research 11(4), pp. 1242-1257'''
Bruun addresses the question: How is erosion, due to loss of sand, distributed downdrift as a function of time? He identifies the length of the downdrift shoreline, the cross-sectional retreat of the erosion cut and the rate of expansion of erosion and its distribution downdrift as functions of time. Previous research related to these areas is included in Bruuns discussion. Bruun defines short term and long term erosion effects where the short term effect is a coastal geomorphological feature and the long distance erosion is a materials deficit feature. Bruun presents examples of downdrift shoreline developments at various global locations with a variety of histories and anthropogenic and non-anthropogenic influences these locations are:


• Port Canaveral, FL
• Port St. Lucie, FL
• Lagos Nigeria
• Hirtshals, Denmark
• Indian River, Delaware
• The southwest coast of France
• Nile Delta
• Skasen Denmark
• Rollover Pass, TX
• Cape May Inlet to Cape May Point, NJ
• Sebastian Inlet, FL
• Ft. Pierce Inlet, FL
• South Lake Worth Inlet, FL
• Iioka Port and Beach, Japan
• Oarai Port and Beach, Japan
• Ocean City Inlet, MD
• Charleston Harbor


The short and long term disturbance effects of the erosion is quantified at these inlets and the connection between the short and long term distance development of downdrift erosion is discussed and quantified through example and explanation of models developed by Perlin and Dean (1978). Also discussed is a zero or slowdown area which is an area of near zero erosion which occasionally exists between the areas of short and long distance development.
Back to [[Inlets | Inlets Geospatial Databases]]

Latest revision as of 17:20, 29 February 2012

UNDER CONSTRUCTION


A literature review of several topic papers on inlet geomorphic parameterization and classification are given in the below annotated bibliography. The Papers are categorized by subject matter: 1) Classification, 2) Processes, 3) Relationships, and 4) Structural Response.


Inlet geomorph fig3 Hayes.png

1) Classification

  • Shoreline classification based upon tide range
    • Microtidal coasts (T.R. 0-2 meters) (wave dominated coasts)
    • Mesotidal coasts (T.R. 2-4 meters)
    • Macrotidal coasts (T.R. > 4 meters) (tide dominated coasts)
  • Variation in inlet planform morphology can be caused by
    • time variation of wave energy
    • time variation of tidal energy (prism),
    • space variation of tidal energy (prism), and
    • evolution of ebb-tidal deltas and adjacent shorelines.


2) Processes

  • Equilibrium properties of coastal structures exist over all time scales and can be used to simplify models and relationships.
  • North Carolina and northern South Carolina are classified as microtidal wave dominated, southern South Carolina and Georgia as mesotidal tide-dominated, and the northeast coast of Florida as microtidal wave dominated.
  • Physical and geological parameters impact tidal inlet variability.
  • The tide dominated inlets are characterized by large ebb-tidal deltas extending far out from shore, well-defined deep main channels and inlet throats, and an absence of inner shoals, except where fresh water inflow induces stratification and landward bottom sediment transport.
  • Sediment is bypassed at inlets through:
    • Stable inlet processes
    • Ebb-tidal delta breaching Inlet migration and spit breaching
    • Outer channel shifting
    • Spit platform breaching
    • Bypassing at wave dominated inlets
    • Jetty-weir bypassing
    • Jettied inlet bypassing
    • Outer channel shifting at jettied inlets
  • Degree of sheltering at an inlet and the back bay environment can effect flood or ebb dominance and create a tidal velocity asymmetry at the inlet. This can, in turn, effect the morphology of the inlet.
  • The direction of tidal forcing was the main parameter governing orientation of the main inlet channel and ebb delta.



3) Relationships

  • The two main principles in bypassing of sand by natural action; bypassing on an offshore bar and bypassing by tidal flow action or a combination of these two methods.
  • The ratio of Mmean/Qmax=r (magnitude of littoral drift) and quantity of flow through the inlet can assist in the identification of these mechanisms. If the ratio is high r>200-300, bar bypassing is predominant. A lower ratio, r<10-20 indicates tidal flow bypassing.
  • A relationship between inlet area and tidal prism of the form A=CPn exists
  • Symmetry is a product of (1) meandering of the channel thalweg, (2) inlet shoreline configuration, and (3) dominant longshore transport direction.
  • A method called the “no-inlet contour method” has been introduced to calculate ebb shoal volumes
  • A relationship is introduced between ebb shoal volume and tidal prism of the form V=aPb
  • The ebb shoal volume appear to be a function of spring tidal prism, inlet area, tidal amplitude and the ratio of inlet width to depth (which arises as a result of the effect of wave induced sediment transport at varying depths over the ebb shoal).
  • Delta growth is explained based upon an analysis of bottom shear stress from current and wave influence (Tb) and the critical stress for scour (Tcr) where, when Tb<< Tcr deposition occurs until they are approximately equal. At this point there is no further deposition and there is an equilibrium water depth above the delta and the delta reaches an equilibrium volume. The influence of wave energy would increase the delta volume (increased wave energy) or decrease the delta volume (decreased wave energy) and the shoal would move away from this equilibrium volume.
  • A linear relationship between the average shoal bypassing event interval (I) and the tidal prism (Tp) was found of the form I=0.046Tp+4.56. It was found that larger inlets undergo shoal bypassing events less frequently than smaller inlets and that the variable I is related to the longshore sediment transport rate.
  • A relationship of the form S=6.42Tp+113.4 has been used to describe the relationship between the average bypassing shoal volume (S) and the tidal prism (P).
  • Four types of inlet instability have been identified: geographic, rotational, meandering and channel stretching.
  • Inlet stability may be thought about in terms of (1) hydraulic parameters (width and length) and (2) positional parameters (migration).
  • Relationships between tidal prism and the planview shape of the ebb shoal have been developed.



4) Structural Responses

  • The introduction of jetties have caused ebb shoals to extend further offshore than previously with a more symmetrical shape.
  • A methodology for determining a net drift direction at a project site was introduced that includes:
    • Office examination of data
    • Field visit with aerial over flight
    • Discussions with specialists
    • Review of wave records
    • Collection of supplemental field data
  • The Inlet reservoir Model (IRM), calculates sediment transport rates and volume change of identified morphologic features and bypassing rates for an inlet.
  • The IRM can be used as an inlet management tool with a general methodology for simulating the evolution of different features and assessing consequences of interruption in sediment transport across inlets.
  • When the combined shear stress (τb) is smaller than the critical shear stress (τcr) deposition will occur until the shear stresses are balanced τb=τcr , when equilibrium is reached.

________________________________________________________________________



Back to Inlets Geospatial Databases

Retrieved from "https://cirpwiki.info/index.php?title=Inlet_Geomorph_Bibliography&oldid=8484"