Culverts: Difference between revisions

From CIRPwiki

Latest revision as of 15:39, 22 October 2012

Representation of Culverts in the CMS
By Christopher Reed and Alejandro Sánchez
Last Modified: September 17, 2010

Introduction

Culverts are a common coastal structure used to increase flushing improve water quality and also provide passage for fish and other aquatic animals to coastal lagoons and bays. The implementation of culverts is based on equations developed by Bodhaine (1982). In coastal applications of culverts, the culverts often connect open water bodies of similar water surface elevation, for instance, to enhance flushing or provide controlled flow through levees or causeways. Therefore, the implementation of culverts assumes sub-critical flow conditions. The implementation of culverts in the CMS is validated in two applications on the lower Mississippi River. The culvert feature is validated with an application to optimize discharges in simulations of the White Ditch diversion in Plaquemines Parish, Louisiana.

Formulation

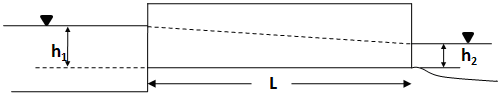
Figure 1. Schematic showing culvert flow conditions.

The representation of culvert flow in the CMS is based on the approach of Bodhaine (1982) and is applied for circular and rectangular culvert cross-sections. Bodhaine describes six types of flow conditions through a culvert that depends on the culvert slope and the upstream and downstream water levels. In most coastal applications of culverts, they are level and the water elevations on either side are similar. These conditions can be considered as ponded upstream and downstream conditions and are most similar to Bodhaine Type 4 flow conditions. A schematic of the typical flow conditions for the culvert is shown in Figure 1. Assuming that the entrance and exit losses are small compared to friction losses in the culvert, the flow equations can be derived from Manning’s equation (using the metric system):

q=C{\frac {AR^{2/3}S^{1/2}}{n}}

(1)

where $q$ is the flow through the culvert, $A$ is the flow cross-sectional area, $R$ is the hydraulic radius, $S$ is the hydraulic gradient, $n$ and is Manning’s.

Coefficient $C$ has been introduced to allow for calibration or representation of other losses. If calibration data is not available then the coefficient $C$ should be set to 1.0.

The hydraulic gradient S is defined as:

S={\frac {h_{1}-h_{2}}{L}}

(2)

where the variables $h_1$, $h_2$, and $L$ are defined in Figure 1.

The hydraulic radius $R$ is defined as the flow area $A$ divided by the wetted perimeter $P$. The values for these variables are dependent on the culvert cross-section and the water depth in the culvert.

Circular Cross-section

Figure 2. Variable definition for circular cross-section.

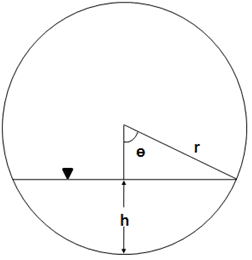
For circular culvert cross-sections, using the definitions in Figure 2, the wetted perimeter and flow area are:

P={\bigg \{}{\begin{smallmatrix}2\theta r,h<r\\2(\pi -\alpha )r,2r>h>r\\2\pi r,h>2r\end{smallmatrix}}\quad {\text{and}}\quad A={\bigg \{}{\begin{smallmatrix}\theta r^{2},h<r\\(\pi -\alpha )r^{2},2r>h>r\\\pi r^{2},h>2r\end{smallmatrix}}

(3)

where $\theta =\cos ^{-1}{{\bigg (}{\frac {r-h}{h}}{\bigg )}}$ and $\alpha =\cos ^{-1}{{\bigg (}{\frac {2r-h}{r}}{\bigg )}}$

Rectangular Cross-section

Figure 3. Variable definition for rectangular cross-section.

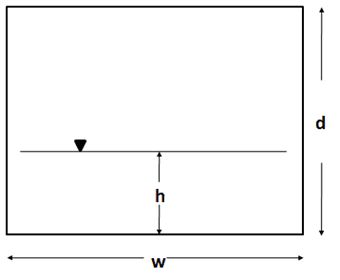
For a rectangular cross-section the wetted perimeter and flow area are:

P={\bigg \{}{\begin{smallmatrix}w+2h,h<d\\2w+2h,h>d\end{smallmatrix}}\quad {\text{and}}\quad A={\bigg \{}{\begin{smallmatrix}wh,h<d\\wd,h>d\end{smallmatrix}}

(4)

where the variables defined as shown in Figure 3.

Flap Gates

The option for including a flap gate at one end of the culvert is also included. For this implementation, flow is limited to the ’downstream’ direction only. If the hydraulic gradient opposes the designated downstream direction (i.e.< 0), the flow is set to zero.

Numerical Implementation

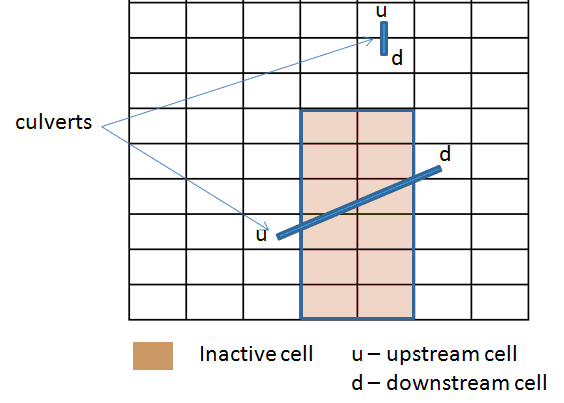
Figure 4. CMS grid and designation of culverts.

The CMS-Flow explicit model uses a staggered grid for the basis of the numerical solution. Two examples of a culvert implementation on the CMS grid are shown in Figure 6. The beginning and end of the culvert are not restricted to adjacent cells and can cross multiple active or inactive cells. A culvert is specified by an upstream and downstream cell, the culvert invert elevation (relative to the model datum), the culvert coefficient

and the culvert shape (circular or rectangular) and associated parameter values. For circular cross-sections, the culvert radius r is specified, and for rectangular cross-sections, the width w and height d are specified. If a flap gate is specified, the flow is limited to the downstream direction. Thus, the upstream and downstream cell designation are important when flap gates are included. The momentum flux of flows through the culverts are assumed to be small and not included in the momentum balance calculations in the CMS solvers. Thus, the culvert flows are only included in the mass balance calculations in the CMS solvers.

Culverts and weirs can be associated with the same CMS cell face and the total flux across the cell face will be the sum of all weirs and culverts specified for that cell face. However, only the fluxes associated with the weirs will be included in the momentum balance.

When salinity or sediment transport is included in simulations with weirs or culverts, the salinity and suspended sediment will be transported. The bedload components in sediment transport algorithms will not be transported over weirs and through culverts.

Additional Information

This CHETN was prepared and funded under the Coastal Inlets Research Program (CIRP) and was written by Dr. Christopher W. Reed (Chris_Reed@URSCorp.com) of URS Corporation. The CIRP Program Manager, Dr. Julie D. Rosati (Julie.D.Rosati@usace.army.mil), the assistant Program Manager, Dr. Nicholas C. Kraus, the Chief of the Coastal Engineering Branch at CHL and Alejandro Sanchez reviewed this CHETN. Files for the example may be obtained by contacting the author.

References

Buttolph, A. M., C. W. Reed, N. C. Kraus, N. Ono, M. Larson, B. Camenen, H. Hanson, T. Wamsley, and A. K. Zundel, A. K. 2006. Two-dimensional depth-averaged circulation model CMS-M2D: Version 3.0, Report 2, sediment transport and morphology change. Coastal and Hydraulics Laboratory Technical Report ERDC/CHL-TR-06-7. Vicksburg, MS: U.S. Army Engineer Research and Development Center.
Bodhaine, G.L., 1982, "Measurement of Peak Discharge at Culverts by Indirect Methods," Techniques of Water Resources Investigations of the United States Geological Survey, Book 3, Chapter A3, U.S. Geological Survey, WA.
Militello, A., Reed, C.W., Zundel, A.K., and Kraus, N.C. 2004. Two-Dimensional Depth-Averaged Circulation Model M2D: Version 2.0, Report 1, Technical Documentation and User’s Guide, ERDC/CHL TR-04-2, U.S. Army Research and Development Center, Coastal and Hydraulics Laboratory, Vicksburg, MS.
URS. 2010. USACE White Ditch evaluation and design – hydrodynamic and salinity transport modeling. URS Corporation, Tallahassee, FL.

Documentation Portal

Retrieved from "https://cirpwiki.info/index.php?title=Culverts&oldid=9219"

Category:

CMS-Flow

@@ Line 1: / Line 1: @@
 __NOTOC__
-<big>
+<font size = "4">'''Representation of Culverts in the CMS'''</font><br>
+<font color=red> '''''By Christopher Reed and Alejandro Sánchez''''' </font><br>
-<font size = "6">'''Representation of Culverts in the Coastal Modeling System'''</font>
+<font color=red> '''''Last Modified: September 17, 2010''''' </font>
-'''''By Christopher Reed and Alejandro Sánchez'''''
-'''''Last Modified: September 17, 2010'''''
-----
-==Purpose==
-This Coastal and Hydraulics Engineering Technical Wiki describes the representation of culverts in the Coastal Modeling System (CMS) operated through the Surface-water Modeling System (SMS).  The CMS is a hydrodynamic and transport model designed for coastal and inlet applications and the SMS is a graphical user interface utility for PCs, developed by the U.S. Army Corps of Engineers (USACE).  The simulation of culverts has been implemented in the CMS-Flow explicit solver.  The mathematical and numerical implementation is described and examples applications are summarized.
 ==Introduction==
 Culverts are a common coastal structure used to increase flushing improve water quality and also provide passage for fish and other aquatic animals to coastal lagoons and bays. The implementation of culverts is based on equations developed by Bodhaine (1982).  In coastal applications of culverts, the culverts often connect open water bodies of similar water surface elevation, for instance, to enhance flushing or provide controlled flow through levees or causeways.  Therefore, the implementation of culverts assumes sub-critical flow conditions.  The implementation of culverts in the CMS is validated in two applications on the lower Mississippi River.  The culvert feature is validated with an application to optimize discharges in simulations of the White Ditch diversion in Plaquemines  Parish, Louisiana.
-== Coastal Modeling System==
-The CMS calculates water levels, currents and waves through the coupling between a hydrodynamic model, CMS-Flow and a wave spectral model, CMS-Wave. These two models can also interact dynamically to simulate sediment and salinity transport, and morphology change (Militello, et&nbsp;al., 2004; Buttolph et&nbsp;al. 2006; Lin et&nbsp;al. 2008).
-CMS‑Flow is a three-dimensional (3D) finite-volume model that solves the mass conservation and shallow-water momentum equations of water motion. The model can run in a two-dimensional (2-D) mode based on the depth-integrated equation. The wave radiation stress and wave field information entering the flow and sediment transport formulas in CMS‑Flow are supplied by CMS‑Wave.  CMS‑Flow is forced by water surface elevation (e.g., from tide), wind and river discharge at the model boundaries, and wave radiation stress and wind field over the model computational domain. Physical processes pertinent to the present study calculated by CMS‑Flow include current, water surface elevation, sediment transport, morphology change, and representation of non-erodible bottom (e.g., reef). Additional capabilities include wetting and drying, spacially varying bottom friction, salinity transport, efficient grid storage in memory, and hot-start options.
-CMS‑Wave is a 2-D steady-state (time-independent) phase-averaged, spectral wave transformation model. The model contains theoretically derived approximations of wave diffraction, reflection, and wave-current interaction for wave simulations at coastal inlets with jetties and breakwaters. It employs a forward-marching and finite-difference method to solve the wave action conservation equation. CMS-Wave operates mainly on a coastal half-plane, so primary waves can propagate only from the seaward boundary toward shore. In the full-plane mode, CMS‑Wave performs the backward-marching for seaward spectral transformation after the forward-marching is completed.
 == Formulation ==
-[[File:Culverts_Figure_1.png|thumb|right|500px|Figure 1.  Schematic showing culvert flow conditions.]]
+[[File:Culverts_Figure_1.png|thumb|right|600px|Figure 1.  Schematic showing culvert flow conditions.]]
 The representation of culvert flow in the CMS is based on the approach of Bodhaine (1982) and is applied for circular and rectangular culvert cross-sections.  Bodhaine describes six types of flow conditions through a culvert that depends on the culvert slope and the upstream and downstream water levels.  In most coastal applications of culverts, they are level and the water elevations on either side are similar.  These conditions can be considered as ponded upstream and downstream conditions and are most similar to Bodhaine Type 4 flow conditions.  A schematic of the typical flow conditions for the culvert is shown in Figure 1.  Assuming that the entrance and exit losses are small compared to friction losses in the culvert, the flow equations can be derived from Manning<nowiki>’</nowiki>s equation (using the metric system):
+{{Equation|<math>q = C \frac{A R^{2/3} S^{1/2} }{ n } </math>|1}}
+where $q$ is the flow through the culvert, $A$ is the flow cross-sectional area, $R$ is the hydraulic radius, $S$ is the hydraulic gradient, $n$ and is Manning<nowiki>’</nowiki>s.
+<br style="clear:both" />
-where is the flow through the culvert, is the cross-section area of the flow, is the hydraulic radius of the flow, is the hydraulic gradient, and is Manning<nowiki>’</nowiki>s .
+Coefficient $C$ has been introduced to allow for calibration or representation of other losses.  If calibration data is not available then the coefficient $C$ should be set to 1.0.
-<br style="clear:both" />
-Coefficient has been introduced to allow for calibration or representation of other losses.  If calibration data is not available then the coefficient should be set to 1.0.
 The hydraulic gradient S is defined as:
+{{Equation|<math>S = \frac{h_1 - h_2 }{ L } </math>|2}}
+where the variables $h_1$, $h_2$, and $L$ are defined in Figure 1.
+<br style="clear:both" />
+The hydraulic radius $R$ is defined as the flow area <math>A</math> divided by the wetted perimeter $P$.  The values for these variables are dependent on the culvert cross-section and the water depth in the culvert.
-where the variable  and are defined in Figure 1.
+=== Circular Cross-section ===
+[[File:Culverts_Figure_2.png|thumb|right|600px|Figure 2.  Variable definition for circular cross-section.]]
+For circular culvert cross-sections, using the definitions in Figure 2, the wetted perimeter and flow area are:
-Figure 2.  Variable definition for circular cross-section.
+{{Equation|<math>
+P = \bigg\{ \begin{smallmatrix}  2 \theta r, h<r \\ 2(\pi-\alpha)r, 2r>h>r  \\ 2 \pi r,   h>2r \end{smallmatrix}\quad \text{and} \quad A = \bigg\{ \begin{smallmatrix} \theta r^2, h<r \\ (\pi-\alpha)r^2, 2r>h>r  \\ \pi r^2,   h>2r \end{smallmatrix}
+</math>|3}}
-The hydraulic radius is defined as the flow area divided by the wetted perimeter.  The values for these variables are dependent on the culvert cross-section and the water depth in the culvert.  For circular culvert cross-sections, using the definitions in Figure 2, the wetted perimeter and flow area are:
-and
-where
-and
+where <math>\theta=\cos^{-1}{ \bigg( \frac{r-h}{h} \bigg) } </math> and  <math>\alpha=\cos^{-1}{ \bigg( \frac{2r-h}{r} \bigg) }</math>
+<br style="clear:both" />
+=== Rectangular Cross-section ===
+[[File:Culverts_Figure_3.png|thumb|right|500px|Figure 3.  Variable definition for rectangular cross-section.]]
 For a rectangular cross-section the wetted perimeter and flow area are:
-and
+{{Equation|<math> P = \bigg\{ \begin{smallmatrix}  w+2h, h<d \\ 2w+2h, h>d  \end{smallmatrix} \quad \text{and} \quad A = \bigg\{ \begin{smallmatrix} wh, h<d \\ wd, h>d  \end{smallmatrix} </math>|4}}
 where the variables defined as shown in Figure 3.
+<br style="clear:both" />
+=== Flap Gates ===
-Figure 3.  Variable definition for rectangular cross-section.
 The option for including a flap gate at one end of the culvert is also included.  For this implementation, flow is limited to the <nowiki>’</nowiki>downstream<nowiki>’</nowiki> direction only. If the hydraulic gradient opposes the designated downstream direction (i.e.<nowiki><</nowiki> 0), the flow is set to zero.
-Figure 4.  CMS grid and designation of culverts.
 == Numerical Implementation ==
-The CMS-Flow model uses a staggered grid for the basis of the numerical solution.  Two examples of a culvert implementation on the CMS grid are shown in Figure 6.  The beginning and end of the culvert are not restricted to adjacent cells and can cross multiple active or inactive cells.  A culvert is specified by an upstream and downstream cell, the culvert invert elevation (relative to the model datum), the culvert coefficient
+[[File:Culverts_Figure_4.png|thumb|right|600px|Figure 4.  CMS grid and designation of culverts.]]
+The CMS-Flow explicit model uses a staggered grid for the basis of the numerical solution.  Two examples of a culvert implementation on the CMS grid are shown in Figure 6.  The beginning and end of the culvert are not restricted to adjacent cells and can cross multiple active or inactive cells.  A culvert is specified by an upstream and downstream cell, the culvert invert elevation (relative to the model datum), the culvert coefficient
 and the culvert shape (circular or rectangular) and associated parameter values.  For circular cross-sections, the culvert radius r is specified, and for rectangular cross-sections, the width w and height d are specified.  If a flap gate is specified, the flow is limited to the downstream direction.  Thus, the upstream and downstream cell designation are important when flap gates are included. The momentum flux of flows through the culverts are assumed to be small and not included in the momentum balance calculations in the CMS solvers.  Thus, the culvert flows are only included in the mass balance calculations in the CMS solvers.
@@ Line 85: / Line 58: @@
 When salinity or sediment transport is included in simulations with weirs or culverts, the salinity and suspended sediment will be transported.  The bedload components in sediment transport algorithms will not be transported over weirs and through culverts.
+<br style="clear:both" />
-== Example Application ==
-Located southeast of New Orleans on the coast of Louisiana, the White Ditch area has been experiencing the shortage of fresh water, sediments and nutrients from the Mississippi River, and saltwater intrusion due to sea level rise and storms.  As a result, extensive wetland loss and degradation of tidal marshes has occurred in the area through the years. A hydrodynamic and salinity modeling analysis was conducted by URS (2010) to evaluate alternative designs for a fresh water diversion from the Mississippi River to the project area.  The alternatives were evaluated in terms of their impact on water depths and salinities throughout the study area.
-Two alternative locations (Locations 2 and 3) are proposed for the diversion near White Ditch.  Location 2 uses a modification of the existing siphon at White Ditch.  Location 3 is located farther to the south.  At both alternative locations different channel depths and widths are considered for different peak diversion flow rates, ranging from 5,000 to 100,000 cfs.  Location 2 also includes culverts located throughout the modified channels to provide connectivity with the marsh areas.
-The alternative design at Location 2 is connected to the Mississippi River with a box culvert and consists of two main outfall channels and three distribution channels, as indicated in Figure 10.  The channels are flanked by levees that constrain the flow within the channels until reaching the downstream ends of the channels.  Culverts are distributed along the channels to provide connectivity to the wetlands, and plugs are placed at some junctures to control the flow.
-At each of the two alternative locations, six design diversion flow rates were considered.  For each flow rate a different channel cross-sectional area was used.  The number of culverts was also varied at Location 2 for each design flow.  Conditions for the six unique grid configurations for Location 2 are shown in Table 5.
-'''Table 5.  Configuration for Location 2 Alternative Designs.'''
-{|border="2" cellspacing="0" cellpadding="4" width="77%" align="left"
-|align = "center"|'''Scenario'''
-|align = "center"|'''White Ditch Diversion Flow Rate (cfs)'''
-|align = "center"|'''Number of Culverts at Each Location'''
-|align = "center"|'''Total Culvert Cross-Sectional Area (ft2)'''
-|-
-|align = "center"|1
-|align = "center"|5,000
-|align = "center"|4 to 8
-|align = "center"|367
-|-
-|align = "center"|2
-|align = "center"|10,000
-|align = "center"|6 to 12
-|align = "center"|551
-|-
-|align = "center"|3
-|align = "center"|15,000
-|align = "center"|10 to 20
-|align = "center"|918
-|-
-|align = "center"|4
-|align = "center"|35,000
-|align = "center"|15 to 30
-|align = "center"|1377
-|-
-|align = "center"|5
-|align = "center"|70,000
-|align = "center"|30 to 60
-|align = "center"|2755
-|-
-|align = "center"|6
-|align = "center"|100,000
-|align = "center"|50 to 100
-|align = "center"|4592
-|}<br clear="all">
-A 2-D CMS-Flow model was developed and calibrated to evaluate each design.  Details of the model configuration and calibration can be found in URS (2010).  The model domain extends about 60 km along the NW-SE directions and about 30 km along the SW-NE direction, and includes the Mississippi River levees, the Mississippi River-Gulf Outlet (MRGO) channel, and other features.  The size of the CMS grid cells ranges from 24 to 600 m with the fine grid along the White Ditch (Mississippi River) and the coarse grid in the Gulf of Mexico.  Figure 11 shows a view of the CMS grid bathymetry in the vicinity of the Location 2 alternative diversion.  The channels and channel elves are evident.  The grid includes specification of the culverts per the alternative design schematics.  The culverts were assumed to have a circular cross-section with 3 foot diameter, and 10 foot length.
-Figure 10.  Culverts designated for Alternative Location 2.
-Figure 11.  CMS Grid bathymetry in vicinity of Alternative Location 2.
-The CMS model boundary conditions included tidal elevations at the offshore boundary, freshwater flow at the Caernarvon Diversion, and freshwater inputs at the proposed White Ditch diversion.  Tide data from the U.S. Geological Survey (USGS) station (7374527) at Northeast Bay Gardene near Point-A-LA-Hache, LA was used as the tide boundary.  Freshwater flows were measured by the New Orleans District, USACE, and were used at the Caernarvon flow boundary.
-Figure 12 shows a time-series of snap shots of the freshwater flowing from the diversion, through the diversion channels and into the wetlands.  The flow through the culverts is evident at each culvert location as indicated by the growing freshwater area.
-Figure 12.  CMS Simulation results showing freshwater discharging through culverts.
-== Conclusions ==
-A representation circular or rectangular culverts has been implemented in the CMS explicit solver.  The algorithms have been tested and validated in field scale examples.  The representation of these structures in the CMS is intended to provide a simple but theoretical basis for simulating their effects on the hydrodynamics and salinity and sediment transport in coastal applications.  The algorithms are not intended to support detailed design of structures, and their use in CMS simulations should consider these limitations.
 == Additional Information ==
@@ Line 173: / Line 69: @@
 *Militello, A., Reed, C.W., Zundel, A.K., and Kraus, N.C.  2004.  Two-Dimensional Depth-Averaged Circulation Model M2D: Version 2.0, Report 1, Technical Documentation and User<nowiki>’</nowiki>s Guide, ERDC/CHL TR-04-2, U.S. Army Research and Development Center, Coastal and Hydraulics Laboratory, Vicksburg, MS.
 *URS. 2010. USACE White Ditch evaluation and design – hydrodynamic and salinity transport modeling. URS Corporation, Tallahassee, FL.
 ----