Filter1d: Difference between revisions
| (36 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
==Purpose== | ==Purpose== | ||
The Coastal Inlets Research Program Technical Wiki herein describes a desktop computer program for filtering and preprocessing time series in support of numerical modeling applications. The utility is | The Coastal Inlets Research Program Technical Wiki herein describes a desktop computer program for filtering and preprocessing time series in support of numerical modeling applications. The utility is provided as a Matlab script and a compiled stand alone executable. The graphical user interface is designed to be extremely easy to use. | ||
==Introduction== | ==Introduction== | ||
| Line 13: | Line 13: | ||
The main feature of the software is the ability to apply high-pass, low-pass, band-pass, and band-stop filters to time series. There are many types of filters | The main feature of the software is the ability to apply high-pass, low-pass, band-pass, and band-stop filters to time series. There are many types of filters in literature, and each have their own advantages and disadvantages. Filter1D uses a windowed sinc filter which is a non-recursive finite impulse response filter. Non-recursive filters consist of convolving the input time series with a weight function and therefore only depend on non-filtered data points. Recursive filters use neighboring filtered points and therefore require stepping or iterations. The advantage non-recursive filters compared to recursive filters is that they are more stable and mathematically simpler. Their disadvantage is that they may require a large number of weights to achieve a desired filter response (amplitude reduction in frequency domain). If the weights are symmetric, then an equal weight is given to points to the left and to the right of a given point and the filter is said to be symmetric and therefore produces no phase lag. | ||
An ideal filter response is a step function. The inverse Fourier transform of an idealized filter response is given by the sinc function. Because the sinc | An ideal filter response is a step function. The inverse Fourier transform of an idealized filter response is given by the sinc function. Because the sinc function extends to minus and positive infinity it must be truncated to be used numerically. The truncation produces a ripple effect (Gibbs phenomenon) in the response function. By multiplying the sinc function with a tapered window such as a Gaussian function, the discontinuities at the ends of the filter are reduced and thus improving the filter response. Several symmetric windows are available in Filter1D including the Hanning, Blackman and Lanczos windows. | ||
Just as in the case of a moving average, special treatment is required for filtering time series near boundaries (begging and end). In Filter1D, an extrapolation technique is used in which an inverted mirror copy of the data is placed before and after the time series. This technique is simple and produces generally good results. Filtering also requires uniformly spaced data (no gaps). Non-uniformly spaced time series are interpolated in Filter1D using linear interpolation. If gaps are present larger than a user specified threshold, than the data is divided into separate time series. | |||
However, preprocessing time series rarely involves just smoothing (filtering). In many cases it is important to determine and remove bad data points (outliers) through interpolation. Filter1D uses two methods for determining outliers. The first is based on the absolute differences (residuals) between the filtered and raw time series. Any data points which exceed a user specified threshold is flagged as an outlier and indicated by cyan colored boxed. The second method uses the magnitude of the finite difference approximation of the second order time derivative. The default thresholds are based on the standard deviation of the residuals and second derivatives and can be changed by the user. | |||
Besides filtering and quality control, the most common preprocessing procedures for preparing numerical model time series include transformations such as unit or datums conversions, cropping, and format conversions. Filter1D provides a simple calculator in which the user may type in any Matlab compatible statement using the time ''t'' and data value ''x'' variables such as ''x'' = 1.3*''x''-0.01, ''t''=60*''t'', or ''x''=''x''(''t''>=100). | |||
<br style="clear:both" /> | <br style="clear:both" /> | ||
==Input Files== | ==Input Files== | ||
Filter1D | Filter1D supports several input file formats including SMS compatible formats, and allows users to import generic ASCII files by specifying the file format interactively. | ||
=== Time Series Data File === | === Time Series Data File === | ||
| Line 64: | Line 73: | ||
=== TAP Microsoft Excel Worksheet === | === TAP Microsoft Excel Worksheet === | ||
[[Image:Filter1D_Figure1.png|thumb|right|400px|Figure 1. Example format for a TAPs Microsoft Excel Worksheet]] | [[Image:Filter1D_Figure1.png|thumb|right|400px|Figure 1. Example format for a TAPs Microsoft Excel Worksheet (Format B).]] | ||
These files consist of an array of water level data entered on a Microsoft Excel workbook (*.xls). Filter1D allows the user to choose the input worksheet and therefore the worksheets contained within the Excel file may be any order. The format of the worksheet should be as follows. The first line is reserved as a header line usually used to describe data columns. The actual content of the header is not actually read by Filter1D and is therefore only for user<nowiki>’</nowiki>s information. Two separate formats are available for the data columns: | These files consist of an array of water level data entered on a Microsoft Excel workbook (*.xls). Filter1D allows the user to choose the input worksheet and therefore the worksheets contained within the Excel file may be any order. The format of the worksheet should be as follows. The first line is reserved as a header line usually used to describe data columns. The actual content of the header is not actually read by Filter1D and is therefore only for user<nowiki>’</nowiki>s information. Two separate formats are available for the data columns: | ||
*Format A. | |||
:Col. 1 - Record number, station number or Julian day (not used in calculations) | |||
:Col. 2 - Date in Excel month-day-year-time format (3/14/01 13:30) | |||
:Col. 3 – Water level in feet or meters (Columns <nowiki>></nowiki> 3 must be empty) | |||
*Format B | |||
:Col. 1 - Record number, station number or Julian day (not used in calculations) | |||
:Col. 2 - Date in Excel month-day-year format (3/14/01) | |||
:Col. 3 - Local Standard Time in Excel 24-hour time format (13:30) | |||
:Col. 4 – Water level in meters or feet | |||
A set of non-numeric column labels may be inserted as the first row of either array. Note that a 4<sup>th</sup> column is not allowed when using format A. Additional metadata such as instrument type, location etc. should be stored in separate worksheets. | A set of non-numeric column labels may be inserted as the first row of either array. Note that a 4<sup>th</sup> column is not allowed when using format A. Additional metadata such as instrument type, location etc. should be stored in separate worksheets. | ||
<br style="clear:both" /> | <br style="clear:both" /> | ||
=== TAP<nowiki>’</nowiki>s Tidal Prediction File=== | === TAP<nowiki>’</nowiki>s Tidal Prediction File=== | ||
The Tidal Analysis and Prediction (TAP) software can perform tidal harmonic analysis and predictions of water levels and currents. The file format for tidal predictions contains 6 header lines with information on the file name, analysis length, tidal constituents used, goodness of fit parameters and vertical datums. The first column of data is the Julian day in Local Standard Time and the following three columns contain the observed, predicted and residual time series of water levels. Below is an example of the file format of a TAP<nowiki>’</nowiki>s Tidal Prediction File | The Tidal Analysis and Prediction (TAP) software can perform tidal harmonic analysis and predictions of water levels and currents. The file format for tidal predictions contains 6 header lines with information on the file name, analysis length, tidal constituents used, goodness of fit parameters and vertical datums. The first column of data is the Julian day in Local Standard Time and the following three columns contain the observed, predicted and residual time series of water levels. Below is an example of the file format of a TAP<nowiki>’</nowiki>s Tidal Prediction File | ||
:NAPL20010111.txt -- 20 day analysis -- <br> | :NAPL20010111.txt -- 20 day analysis -- <br> | ||
| Line 89: | Line 108: | ||
==Getting Started== | ==Getting Started== | ||
[[Image:Filter1D_Figure2.png| | [[Image:Filter1D_Figure2.png|thumb|right|600px|Figure 2. Filter1D interface showing an idealized input time series]] | ||
Filter1D | Filter1D can be launched either from the Matlab script filter1d.m or the stand alone application filter1d.exe. The stand alone version requires the installation of the Matlab Component Runtime Installer MCRinstaller.exe. This file contains the Matlab libraries needed to run the program. There are two options to open the Filter1D utility. The first is by clicking on the menu Data <nowiki>|</nowiki> Analysis <nowiki>|</nowiki> 1D Filter. The Filter1D interface will appear with an idealized time series as shown in Figure 2. The time series consists of three tidal harmonic constituents M2 (1.9324 cpd), O1 (0.9295 cpd), and M4 (3.8647 cpd) plus additional white noise. The upper right plot shows the computed amplitude spectra as a function of frequency (cpd). Because the white noise energy is distributed in a wide range of frequencies, it does not appear to be significant in the amplitude spectra. However, from the time series plot, it is clear the quality of the signal is significantly reduced by the presence of noise. | ||
<br style="clear:both" /> | |||
[[Image:Filter1D_Figure3.png|thumb|right|600px|Figure 3. Filter1D interface showing the filtered idealized input time series]] | |||
To filter the time series, simply click on the button labeled ''Apply''. The resulting window is shown in Figure 3. In the menu which reads ''Windowed Sinc Filter'', ''Window'' indicates the window used with the sinc function in the filter and ''Type'' indicates the type of filter and is either low-pass, high-pass and band-pass. ''Cut-Off Freq.'' indicates the cut-off frequency in the cases for low-pass and high-pass filters and the central frequency for Band-Pass filter. ''Length'' indicates the length of the filter or the number of weights used so that n = 2*''Length''<nowiki>+</nowiki>1 is the number of weights in the filter. The filtered time series will automatically be displayed in red in the lower plot. The amplitude spectrum plot will show an additional red line which corresponds to the calculated amplitude spectra of the filtered time series and allows the user to see how much energy has been removed from the time series in the frequency domain. Overlaid on the amplitude spectra plot is the filter response curve. The cut-off frequency is shown as a vertical line in the sample plot. | |||
Although the original and filtered amplitude spectra are quite similar the reduction in noise is evident in the time series plot. It is recommended that the user experiment with the many functions and options available using at this stage. For example, the data cursor located in the menu bar may be used to click on any point of the time series or amplitude spectra plots to obtain the x- and y-values. The zoom in, zoom out, and panning tools are useful for viewing specific portions of long time series and inspecting the data for outliers. The markers (points) for the input and filtered time series can be displayed by selecting the option ''Line Markers'' under the View menu. It is recommended that the user change the filter settings inside the box labels "Windowed Sinc Filter" to get a good "feeling" for how the filter works. | |||
<br style="clear:both" /> | |||
== Example Application == | |||
As an example, a water level time series measured by an Acoustic Doppler Profiler or ADP at Blind Pass, FL [[Blind_Pass.rar | Blind_Pass.tsd]] is analyzed and prepared for use in the Coastal Modeling System circulation model CMS-Flow. | |||
As an example, a water level time series measured by an Acoustic Doppler Profiler or ADP at Blind Pass, FL is analyzed and prepared for use in the Coastal Modeling System circulation model CMS-Flow | |||
===Loading Data and Initial Inspection=== | ===Loading Data and Initial Inspection=== | ||
[[Image: | [[Image:Filter1D_Figure4.png|thumb|right|500px|Figure 4. Example of a dialog window for opening input files.]] | ||
To load the data file, click on the button | To load the data file [[Media:Blind_Pass.rar | Blind_Pass.tsd]], click on the button labeled ''Browse'' and a window will appear as in Figure 4. Go to the folder where the input file is located, select the file and click on ''Open'' or simply double-click on the file. | ||
A dialog window will appear indicating that variables time steps have been identified. Since the filtering algorithm requires data spaced at regular intervals, the data must be interpolated to eliminate small data gaps, time shifts or changing in the sampling interval. The user will also be prompted to input the maximum interval for interpolation. The data is subsequently cropped to the first interval exceeding this value. By cropping the data in this way, the interpolation of large gaps is avoided which can introduce errors in the filter algorithm. | |||
[[Image:Filter1D_Figure5.png|thumb|right|600px|Figure 5. Filter1D window with imported water level time series for Blind Pass, FL]] | |||
Once, the data is loaded, the Filter1D window should view as in Figure 4. The amplitude spectrum shows two distinct peaks at approximately 0.98 cpd and 1.93 cpd which correspond to the K1 and M2 tidal constituents respectively. | Once, the data is loaded, the Filter1D window should view as in Figure 4. The amplitude spectrum shows two distinct peaks at approximately 0.98 cpd and 1.93 cpd which correspond to the K1 and M2 tidal constituents respectively. | ||
<br style="clear:both" /> | <br style="clear:both" /> | ||
===Initial Outlier Detection=== | ===Initial Outlier Detection=== | ||
Even before performing any filtering, the user may want to identify outliers and remove them from the time series. This is done by using maximum absolute value of the time series second derivative Points which exceed a user specified threshold are designated as possible outliers are highlighted with cyan colored squares. To identify possible outliers, click on Tools <nowiki>|</nowiki> Find Outliers. A window dialog will appear promting the user the input a threshold value. If the OK button is pressed, the points which exceed the threshold are highlighted but not deleted. In order to delete the points, the user must manually delete individual points by using the ''Delete Points'' tool under the ''Edit'' menu. To delete points, left-click on a point and a green circle will appear on the data point closest to the point clicked. An additional left-click on the point will remove it and linearly re-interpolate it. The default threshold is equal to four times the standard deviation of the maximum absolute second derivative for the whole time series. | Even before performing any filtering, the user may want to identify outliers and remove them from the time series. This is done by using maximum absolute value of the time series second derivative Points which exceed a user specified threshold are designated as possible outliers are highlighted with cyan colored squares. To identify possible outliers, click on Tools <nowiki>|</nowiki> Find Outliers. A window dialog will appear promting the user the input a threshold value. If the OK button is pressed, the points which exceed the threshold are highlighted but not deleted. In order to delete the points, the user must manually delete individual points by using the ''Delete Points'' tool under the ''Edit'' menu. To delete points, left-click on a point and a green circle will appear on the data point closest to the point clicked. An additional left-click on the point will remove it and linearly re-interpolate it. The default threshold is equal to four times the standard deviation of the maximum absolute second derivative for the whole time series. | ||
===Filtering=== | ===Filtering=== | ||
[[Image: | [[Image:Filter1D_Figure6.png|thumb|right|600px|Figure 6. Filter1D window showing the imported and filtered water level time series for Blind Pass, FL]] | ||
After clicking on the ''Apply'' button, the filtered time series and amplitude spectra will be displayed in red color. It is important to check that the cut-off frequency is adequate and that energy is not being removed at frequencies near the range of interest, in this, astronomical tides. The highest frequency of interest in case is the M4 tides (3.867 cpd). Therefore, a cut-off frequency of 5 cpd should be adequate. The best way of checking that the frequencies of interest are not being modified is by examining the amplitude spectra and filter response curve. It is also recommended to closely examine the time series by panning through sections of it after trying different cut-off frequencies and filter lengths to make sure that the user implements the optimal filter settings. In general, the closer the cut-off frequency is the frequencies of interest the sharper the response function must be and therefore the larger number of filter coefficients required. The disadvantage of using a larger number of filter coefficients is that the, the computation increases but mainly that the filter may have problems with start and ending of the time series. Filter1D automatically sets limits to the length of the filter. | After clicking on the ''Apply'' button, the filtered time series and amplitude spectra will be displayed in red color. It is important to check that the cut-off frequency is adequate and that energy is not being removed at frequencies near the range of interest, in this, astronomical tides. The highest frequency of interest in case is the M4 tides (3.867 cpd). Therefore, a cut-off frequency of 5 cpd should be adequate. The best way of checking that the frequencies of interest are not being modified is by examining the amplitude spectra and filter response curve. It is also recommended to closely examine the time series by panning through sections of it after trying different cut-off frequencies and filter lengths to make sure that the user implements the optimal filter settings. In general, the closer the cut-off frequency is the frequencies of interest the sharper the response function must be and therefore the larger number of filter coefficients required. The disadvantage of using a larger number of filter coefficients is that the, the computation increases but mainly that the filter may have problems with start and ending of the time series. Filter1D automatically sets limits to the length of the filter. | ||
<br style="clear:both" /> | |||
== Additional Information== | == Additional Information== | ||
| Line 165: | Line 149: | ||
---- | ---- | ||
[[Utilities | CMS Utilities]] | |||
[[ | |||
| | |||
Latest revision as of 14:27, 11 October 2010
Filter1D - Time Series Analysis Tool
By Alejandro Sánchez
Purpose
The Coastal Inlets Research Program Technical Wiki herein describes a desktop computer program for filtering and preprocessing time series in support of numerical modeling applications. The utility is provided as a Matlab script and a compiled stand alone executable. The graphical user interface is designed to be extremely easy to use.
Introduction
Preprocessing and quality control of input time series for surface water flow and sediment transport numerical models are key steps in setting up the simulations and obtaining correct results. In the past, users of the SMS have performed these tasks using external software such as MATLAB® or EXCEL® and required several steps. The software presented herein, provides users of the SMS, a one-stop package for preparing model input time series and allows users to interpolate, resample, filter, and transform any type of model forcing and supports SMS compatible file formats for ease of data transfer.
The main feature of the software is the ability to apply high-pass, low-pass, band-pass, and band-stop filters to time series. There are many types of filters in literature, and each have their own advantages and disadvantages. Filter1D uses a windowed sinc filter which is a non-recursive finite impulse response filter. Non-recursive filters consist of convolving the input time series with a weight function and therefore only depend on non-filtered data points. Recursive filters use neighboring filtered points and therefore require stepping or iterations. The advantage non-recursive filters compared to recursive filters is that they are more stable and mathematically simpler. Their disadvantage is that they may require a large number of weights to achieve a desired filter response (amplitude reduction in frequency domain). If the weights are symmetric, then an equal weight is given to points to the left and to the right of a given point and the filter is said to be symmetric and therefore produces no phase lag.
An ideal filter response is a step function. The inverse Fourier transform of an idealized filter response is given by the sinc function. Because the sinc function extends to minus and positive infinity it must be truncated to be used numerically. The truncation produces a ripple effect (Gibbs phenomenon) in the response function. By multiplying the sinc function with a tapered window such as a Gaussian function, the discontinuities at the ends of the filter are reduced and thus improving the filter response. Several symmetric windows are available in Filter1D including the Hanning, Blackman and Lanczos windows.
Just as in the case of a moving average, special treatment is required for filtering time series near boundaries (begging and end). In Filter1D, an extrapolation technique is used in which an inverted mirror copy of the data is placed before and after the time series. This technique is simple and produces generally good results. Filtering also requires uniformly spaced data (no gaps). Non-uniformly spaced time series are interpolated in Filter1D using linear interpolation. If gaps are present larger than a user specified threshold, than the data is divided into separate time series.
However, preprocessing time series rarely involves just smoothing (filtering). In many cases it is important to determine and remove bad data points (outliers) through interpolation. Filter1D uses two methods for determining outliers. The first is based on the absolute differences (residuals) between the filtered and raw time series. Any data points which exceed a user specified threshold is flagged as an outlier and indicated by cyan colored boxed. The second method uses the magnitude of the finite difference approximation of the second order time derivative. The default thresholds are based on the standard deviation of the residuals and second derivatives and can be changed by the user.
Besides filtering and quality control, the most common preprocessing procedures for preparing numerical model time series include transformations such as unit or datums conversions, cropping, and format conversions. Filter1D provides a simple calculator in which the user may type in any Matlab compatible statement using the time t and data value x variables such as x = 1.3*x-0.01, t=60*t, or x=x(t>=100).
Input Files
Filter1D supports several input file formats including SMS compatible formats, and allows users to import generic ASCII files by specifying the file format interactively.
Time Series Data File
The first file format which is supported in Filter1D is the Time Series Data file (*.tsd). This file is supported in SMS versions 10.1+. The ASCII file consists of two header lines followed by data columns separated by spaced or tabs. The first line contains the identifier TIMESERIES. The second line should contain 5 elements. The first element of the second line is the name of the time series within apostrophes. The second element specifies the curve type and may be either "Unassigned", "Vel. & Mag.", or "Vel. Components". The third element is an integer specifying the number of input columns including the time stamp (column 1). The forth element is the length of the input time series. The fifth element is the date and time of the start of the time series within apostrophes, specified as "mm/dd/yyy HH:MM:SS" where mm is the month, dd is the day, HH is the hour, MM is the minute, and SS is the seconds. The input time series does not need to have a regular time interval.
- TIME_SERIES
- "CRCR2007" "Unassigned" 2 1535 "03/01/2007 00:00:00"
- 0.00 0.227
- 1800.00 0.198
- 3600.00 0.168
- 5400.00 0.137
- 7200.00 0.104
- 9000.00 0.070
- 10800.00 0.036
XY Series File
The XY Series file is an ASCII file used in SMS versions 10.0+ which contains time series data in a simple compact format. The first line of the file contains a header with four elements. The first is the letter XYS indicating the file type, the second is a file identifier number. The third element indicates the length of the input time series and the forth is the time series name within apostrophes. An example of an XY Series file is shown below
- XYS 1 5 "Curve"
- 0.0 3.864877777
- 0.01 -8.37412494
- 0.03 -10.98672748
- 0.04 -16.76807057
- 0.06 -15.35866559
NOAA CO-OPS File
The National Oceanic and Atmospheric Administration (NOAA) Center for Operational Oceanographic Products and Services (CO-OPS) Tides and Currents website http://www.co-ops.nos.noaa.gov/index.shtml provides water surface elevation and currents and historical and active stations all over the United States. The user may use directly import water surface elevation data copied directly from this website using the NOAA CO-OPS file format shown below
- Tide DataStation Date Time Pred 6 Acoustc
- DCP#: 1 1
- Units: Meters Meters
- Data%: MSL GMT 100.000 99.382
- Maximum: 0.779 0.945
- Minimum: -0.786 -0.755
- ------- -------- ----- ------- -------
- 8639207 20070301 00:00 0.222 0.279
- 8639207 20070301 00:06 0.207 0.261
- 8639207 20070301 00:12 0.191 0.245
- 8639207 20070301 00:18 0.175 0.224
TAP Microsoft Excel Worksheet
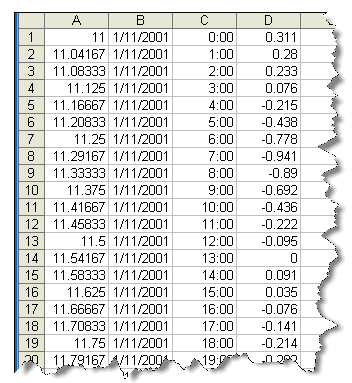
These files consist of an array of water level data entered on a Microsoft Excel workbook (*.xls). Filter1D allows the user to choose the input worksheet and therefore the worksheets contained within the Excel file may be any order. The format of the worksheet should be as follows. The first line is reserved as a header line usually used to describe data columns. The actual content of the header is not actually read by Filter1D and is therefore only for user’s information. Two separate formats are available for the data columns:
- Format A.
- Col. 1 - Record number, station number or Julian day (not used in calculations)
- Col. 2 - Date in Excel month-day-year-time format (3/14/01 13:30)
- Col. 3 – Water level in feet or meters (Columns > 3 must be empty)
- Format B
- Col. 1 - Record number, station number or Julian day (not used in calculations)
- Col. 2 - Date in Excel month-day-year format (3/14/01)
- Col. 3 - Local Standard Time in Excel 24-hour time format (13:30)
- Col. 4 – Water level in meters or feet
A set of non-numeric column labels may be inserted as the first row of either array. Note that a 4th column is not allowed when using format A. Additional metadata such as instrument type, location etc. should be stored in separate worksheets.
TAP’s Tidal Prediction File
The Tidal Analysis and Prediction (TAP) software can perform tidal harmonic analysis and predictions of water levels and currents. The file format for tidal predictions contains 6 header lines with information on the file name, analysis length, tidal constituents used, goodness of fit parameters and vertical datums. The first column of data is the Julian day in Local Standard Time and the following three columns contain the observed, predicted and residual time series of water levels. Below is an example of the file format of a TAP’s Tidal Prediction File
- NAPL20010111.txt -- 20 day analysis --
- Start Date/Time(LST): 11-Jan-2001 00:00:00 11
- Tides: O1 K1 MNS2 N2 M2 S2 MK3 MN4 M4 S4 2MS6
- RMS= 0.099 %R_var= 86.42
- Mean water level: -0.1851 meters
- JDay(LST) Observed Predicted Residual
- 11.000000 0.3110 0.3257 -0.0147
- 11.041667 0.2800 0.3162 -0.0362
- 11.083333 0.2330 0.2213 0.0117
- 11.125000 0.0760 0.0387 0.0373
- 11.166667 -0.2150 -0.2053 -0.0097
Getting Started
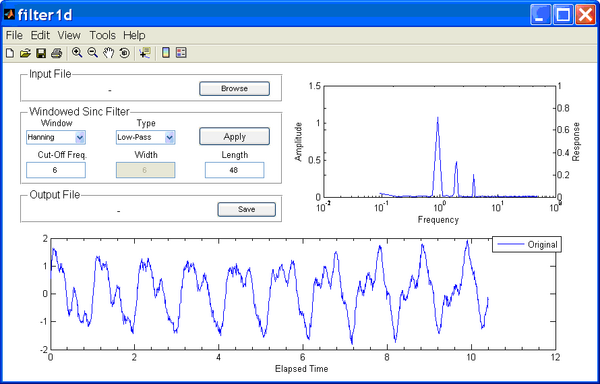
Filter1D can be launched either from the Matlab script filter1d.m or the stand alone application filter1d.exe. The stand alone version requires the installation of the Matlab Component Runtime Installer MCRinstaller.exe. This file contains the Matlab libraries needed to run the program. There are two options to open the Filter1D utility. The first is by clicking on the menu Data | Analysis | 1D Filter. The Filter1D interface will appear with an idealized time series as shown in Figure 2. The time series consists of three tidal harmonic constituents M2 (1.9324 cpd), O1 (0.9295 cpd), and M4 (3.8647 cpd) plus additional white noise. The upper right plot shows the computed amplitude spectra as a function of frequency (cpd). Because the white noise energy is distributed in a wide range of frequencies, it does not appear to be significant in the amplitude spectra. However, from the time series plot, it is clear the quality of the signal is significantly reduced by the presence of noise.
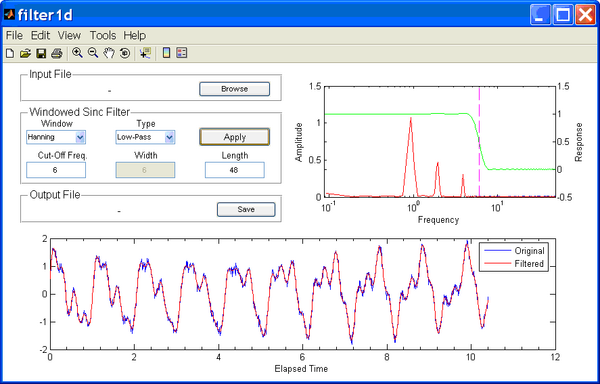
To filter the time series, simply click on the button labeled Apply. The resulting window is shown in Figure 3. In the menu which reads Windowed Sinc Filter, Window indicates the window used with the sinc function in the filter and Type indicates the type of filter and is either low-pass, high-pass and band-pass. Cut-Off Freq. indicates the cut-off frequency in the cases for low-pass and high-pass filters and the central frequency for Band-Pass filter. Length indicates the length of the filter or the number of weights used so that n = 2*Length+1 is the number of weights in the filter. The filtered time series will automatically be displayed in red in the lower plot. The amplitude spectrum plot will show an additional red line which corresponds to the calculated amplitude spectra of the filtered time series and allows the user to see how much energy has been removed from the time series in the frequency domain. Overlaid on the amplitude spectra plot is the filter response curve. The cut-off frequency is shown as a vertical line in the sample plot.
Although the original and filtered amplitude spectra are quite similar the reduction in noise is evident in the time series plot. It is recommended that the user experiment with the many functions and options available using at this stage. For example, the data cursor located in the menu bar may be used to click on any point of the time series or amplitude spectra plots to obtain the x- and y-values. The zoom in, zoom out, and panning tools are useful for viewing specific portions of long time series and inspecting the data for outliers. The markers (points) for the input and filtered time series can be displayed by selecting the option Line Markers under the View menu. It is recommended that the user change the filter settings inside the box labels "Windowed Sinc Filter" to get a good "feeling" for how the filter works.
Example Application
As an example, a water level time series measured by an Acoustic Doppler Profiler or ADP at Blind Pass, FL Blind_Pass.tsd is analyzed and prepared for use in the Coastal Modeling System circulation model CMS-Flow.
Loading Data and Initial Inspection
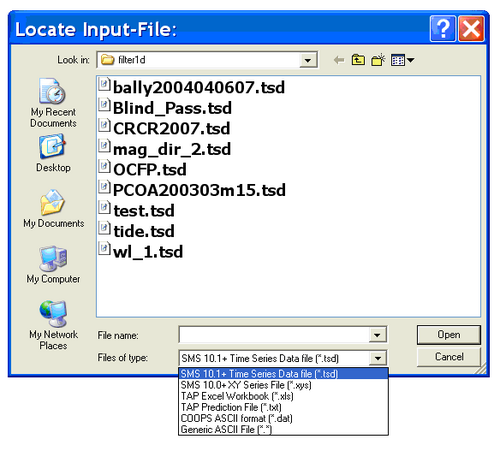
To load the data file Blind_Pass.tsd, click on the button labeled Browse and a window will appear as in Figure 4. Go to the folder where the input file is located, select the file and click on Open or simply double-click on the file.
A dialog window will appear indicating that variables time steps have been identified. Since the filtering algorithm requires data spaced at regular intervals, the data must be interpolated to eliminate small data gaps, time shifts or changing in the sampling interval. The user will also be prompted to input the maximum interval for interpolation. The data is subsequently cropped to the first interval exceeding this value. By cropping the data in this way, the interpolation of large gaps is avoided which can introduce errors in the filter algorithm.
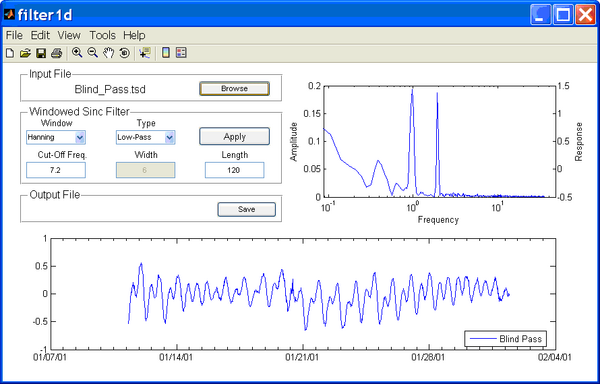
Once, the data is loaded, the Filter1D window should view as in Figure 4. The amplitude spectrum shows two distinct peaks at approximately 0.98 cpd and 1.93 cpd which correspond to the K1 and M2 tidal constituents respectively.
Initial Outlier Detection
Even before performing any filtering, the user may want to identify outliers and remove them from the time series. This is done by using maximum absolute value of the time series second derivative Points which exceed a user specified threshold are designated as possible outliers are highlighted with cyan colored squares. To identify possible outliers, click on Tools | Find Outliers. A window dialog will appear promting the user the input a threshold value. If the OK button is pressed, the points which exceed the threshold are highlighted but not deleted. In order to delete the points, the user must manually delete individual points by using the Delete Points tool under the Edit menu. To delete points, left-click on a point and a green circle will appear on the data point closest to the point clicked. An additional left-click on the point will remove it and linearly re-interpolate it. The default threshold is equal to four times the standard deviation of the maximum absolute second derivative for the whole time series.
Filtering
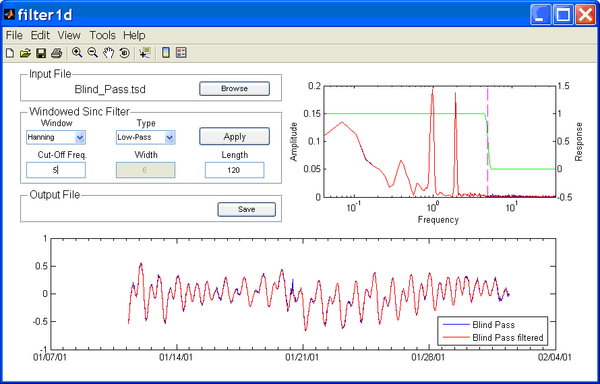
After clicking on the Apply button, the filtered time series and amplitude spectra will be displayed in red color. It is important to check that the cut-off frequency is adequate and that energy is not being removed at frequencies near the range of interest, in this, astronomical tides. The highest frequency of interest in case is the M4 tides (3.867 cpd). Therefore, a cut-off frequency of 5 cpd should be adequate. The best way of checking that the frequencies of interest are not being modified is by examining the amplitude spectra and filter response curve. It is also recommended to closely examine the time series by panning through sections of it after trying different cut-off frequencies and filter lengths to make sure that the user implements the optimal filter settings. In general, the closer the cut-off frequency is the frequencies of interest the sharper the response function must be and therefore the larger number of filter coefficients required. The disadvantage of using a larger number of filter coefficients is that the, the computation increases but mainly that the filter may have problems with start and ending of the time series. Filter1D automatically sets limits to the length of the filter.
Additional Information
Questions about this CHETN can be addressed Alex Sánchez at (601-634-2027), FAX (601-634-3433), or e-mail: [mailto: Alejandro.Sanchez@usace.army.mil Alejandro.Sanchez@usace.army.mil]. This Technical Note should be referenced as follows: