Weirs: Difference between revisions

From CIRPwiki
Jump to navigation Jump to search
No edit summary
No edit summary
 
(23 intermediate revisions by 3 users not shown)
Line 1: Line 1:
__NOTOC__
__NOTOC__
<big>


=='''Representation of Weirs in the Coastal Modeling System''' ==
=='''Representation of Weirs in the CMS''' ==


'''''By Christopher Reed and Alejandro Sánchez'''''
'''''By Christopher Reed and Alejandro Sánchez'''''


Last Date Modified: September 17, 2010
'''''Last Date Modified: September 17, 2010'''''
 
----
 
==Purpose==
This Coastal and Hydraulics Engineering Technical Wiki describes the representation of weirs in the Coastal Modeling System (CMS) operated through the Surface-water Modeling System (SMS).  The CMS is a hydrodynamic and transport model designed for coastal and inlet applications and the SMS is a graphical user interface utility for PCs, developed by the U.S. Army Corps of Engineers (USACE).  The simulation of weirs has been implemented in the CMS-Flow explicit solver.  The mathematical and numerical implementation is described and examples applications are summarized.


==Introduction==
==Introduction==
Weirs are a common coastal engineering structure used to control flow and can affect sediment transport.  They are typically used in weir jetties or in wetlands to control discharges, provide flood control, act as salinity barriers and optimally distribute freshwater to manage salinity regimes and sedimentation rates and deposition patterns.  Since these structures are a significant component of hydrodynamic and sediment transport controls in the coastal zone, it is important that the CMS simulate their effects.  The simulation of weirs is based on the standard weir equation for either sharp-crested or broad-crested weirs, with a foundation in Bernoulli<nowiki>’</nowiki>s equation. The implementation of weirs in the CMS is validated in two applications on the lower Mississippi River.  The weirs are applied in the simulation of flow over the Bonne Carrie spillway north of New Orleans.
Weirs are a common coastal engineering structure used to control flow and can affect sediment transport.  They are typically used in weir jetties or in wetlands to control discharges, provide flood control, act as salinity barriers and optimally distribute freshwater to manage salinity regimes and sedimentation rates and deposition patterns.  Since these structures are a significant component of hydrodynamic and sediment transport controls in the coastal zone, it is important that the CMS simulate their effects.  The simulation of weirs is based on the standard weir equation for either sharp-crested or broad-crested weirs, with a foundation in Bernoulli<nowiki>’</nowiki>s equation. The implementation of weirs in the CMS is validated in two applications on the lower Mississippi River.  The weirs are applied in the simulation of flow over the Bonne Carrie spillway north of New Orleans.


==Coastal Modeling System==
==Formulation==
The CMS calculates water levels, currents and waves through the coupling between a hydrodynamic model, CMS-Flow and a wave spectral model, CMS-Wave. These two models can also interact dynamically to simulate sediment and salinity transport, and morphology change (Militello, et&nbsp;al., 2004; Buttolph et&nbsp;al. 2006; Lin et&nbsp;al. 2008).
Two approaches are developed to implement weir structures in the CMS. In the first approach the standard weir equation for a rectangular crosssection is introduced in the model as follows (HEC 2010):
 


CMS‑Flow is a three-dimensional (3D) finite-volume model that solves the mass conservation and shallow-water momentum equations of water motion. The model can run in a two-dimensional (2-D) mode based on the depth-integrated equation. The wave radiation stress and wave field information entering the flow and sediment transport formulas in CMS‑Flow are supplied by CMS‑Wave.  CMS‑Flow is forced by water surface elevation (e.g., from tide), wind and river discharge at the model boundaries, and wave radiation stress and wind field over the model computational domain. Physical processes pertinent to the present study calculated by CMS‑Flow include current, water surface elevation, sediment transport, morphology change, and representation of non-erodible bottom (e.g., structures). Additional capabilities include wetting and drying, spacially varying bottom friction, salinity transport, efficient grid storage in memory, and hot-start options.
{{Equation|<math>Q = C_{df} C_w L h^{1.5} </math>|1}}


where Q is the flow rate over the weir crest, <math>C_w</math> is the weir coefficient, <math>L_w</math> is the weir crest length, <math>h</math> is the upstream water depth above the crest, and <math>C_{df}</math> is the submergence correction factor (also referred to as the drowned flow reduction factor). A definition schematic for both the free flow and submerged flow conditions is provided in Figure 1.
CMS‑Wave is a 2-D steady-state (time-independent) phase-averaged, spectral wave transformation model. The model contains theoretically derived approximations of wave diffraction, reflection, and wave-current interaction for wave simulations at coastal inlets with jetties and breakwaters. It employs a forward-marching and finite-difference method to solve the wave action conservation equation. CMS-Wave operates mainly on a coastal half-plane, so primary waves can propagate only from the seaward boundary toward shore. In the full-plane mode, CMS‑Wave performs the backward-marching for seaward spectral transformation after the forward-marching is completed.
 
==Formulation==
The Hydraulic Engineering Center (HEC, 2010) approach for calculating flow over rectangular weirs is adopted here.  The form of the weir flow equation as presented in HEC (2010) is:
        {{Equation| <math> Q = C_{df} C_w L h^{1.5} </math>|2=1}}
 
where <math>Q</math> is the flow rate over the weir crest, <math>C_w</math> is the weir coefficient, <math>L</math> is the weir crest length, <math>h</math> is the upstream water depth above the crest, and <math>C_{df}</math> is the submergence correction factor (also referred to as the drowned flow reduction factor). A definition schematic for both the free flow and submerged flow conditions is provided in Figure 1.


[[File:Weirs_Figure_1.png|thumb|left|500px|Figure 1. Schematic showing weir flow conditions.]]
[[File:Weirs_Figure_1.png|thumb|left|500px|Figure 1. Schematic showing weir flow conditions.]]
<br style="clear:both" />
<br style="clear:both" />
An inspection of Equation 1 reveals that the weir coefficient is dimensional. In CMS, the the equation is re-written as:


        {{Equation| <math> Q = C_{df} C'_w \sqrt{g} L h^{1.5} </math>|2=2}}
To obtain a non-dimensional weir coefficient, Equation (1) can be re-written as (Reed and
Sanchez 2011)


where <math>g</math> is the acceleration due to gravity and <math> C'_w = C_w \ \sqrt{g} </math>.  In this form, the coefficients are independent of the measurement system (i.e. Metric or English). The value for the weir coefficient depends on the upstream and downstream geometry of the weir.  Ranges for the coefficient suggested in HEC (2010) are listed in Table 1.0.
{{Equation|<math>Q = C_{df} C'_w \sqrt{g} L h^{1.5} </math>|2}}


<br style="clear:both" />
where <math> C'_w = C_w / \sqrt{g} </math>.  Ranges for <math>C^'_{w}</math> were suggested in HEC (2010). For a sharp-crested weir, it is between 0.55 and 0.58, and a broad-crested weir between 0.46 and 0.55.
'''Table 1.0.  Suggested Weir Coefficient'''''' ''' QUOTE      ''' Values.'''
{|border="2" cellspacing="0" cellpadding="4" width="40%" align="center"
|align = "center"|'''Configuration'''
|align = "center"| QUOTE      '''  Range*'''
|-
|Sharp-crested
|align = "center"|0.55 – 0.58
|-
|Broad-crested
|align = "center"|0.46– 0.55
|}<br clear="all">
<nowiki>*</nowiki> values in HEC (2010) converted to


Super-critical flow conditions occur when the flow is independent of the tail-water elevation.  These conditions occur when the tail-water elevation is sufficiently low that the sub-critical coefficient <math> C_{df} </math> is equal to 1.0. For submerged conditions a different approach is used for setting      .  For sharp-crested weirs, the coefficient is based on the equation by Villemonte (1947):
The submergence coefficient (C<sub>df</sub>) is determined using different methods. For a sharp-crested weir, the Villemonte formula is used,


        {{Equation| <math> C_{df} = 1 - \biggl( \frac{h_2}{h_1} \biggr) ^{1.5) </math>|2=3}}
{{Equation|<math>C_{df} = \Bigg[1 - \biggl( \frac{h_2}{h_1} \biggr) ^{1.5} \Bigg]^{0.385} </math>|3}}


where <math> C'_w = C_w \ \sqrt{g} </math>     and <math> C'_w = C_w \ \sqrt{g} </math>     are defined in Figure 2. For broad-crested weirs, the value of      is calculated by fitting a curve to data from USACE EM 1110-2-1603 (plate 3-5, Section A-A).  An exponential curve was fit to the Section A-A data.  The fit is shown in Figure 2 and the equation for C<sub>df</sub> is:
where <math>h_1</math> and <math> h_2 </math> are the upstream and downstream water levels above the weir crest elevation, respectively. For a broad-crested weir, <math>C_w ^'</math>is calculated as 


[[File:Weirs_Figure_2.png|thumb|left|500px|Figure 2.  Curve fit to the USACE EM 1110-2-1603, plate 3-5, Section A-A data.]]
{{Equation|<math>C_{df} = \left\{
<br style="clear:both" />
\begin{align}
&\quad \quad \quad 1  \quad\quad\quad\quad\quad\quad\quad\quad h_2/h_1 \leq 0.67 \\  
&1 - 27.8(h_2/h_1 - 0.67)^3 \quad h_2/h_1 > 0.67
\end{align}
\right.
</math>|4}}


==Numerical Implementation==
For a spillway-type weir, <math>C_df</math> is obtained by fitting a curve to data (Reed and Sanchez 2011),
The CMS-Flow explicit solver uses a staggered grid for the basis of the numerical solution.  Weirs are implemented on the cell faces by specifying the two adjacent cells.  The order of the cell specification is not critical for the weir implementation since the algorithm implemented in the CMS will determine the flow regime and the flow direction from the specified weir crest elevation and the water elevation in the adjacent cells.  Figure 6 shows a typical CMS grid with a weir specified at a cell face.


[[File:Weirs_Figure_3.png|thumb|left|400px|Figure 3.  CMS grid and designation of weirs.]]
{{Equation|<math> C_{df} = 1 -  \exp{ \biggl(-8.5 \frac{h_d}{h_1} \biggr) }</math>|5}}
<br style="clear:both" />


In addition to the weir location,the user must also specify the crest elevation relative to the model datum, crest length L and the coefficient QUOTE      .  Multiple weirs can be specified at each face and the total flow across the face is the sum of the flow calculated for each individual weir.  The momentum flux associated with the flow over the weir (and subsequently across the CMS cell face) is included in both the mass balance and the momentum balance calculations.  Also, a weir can be specified as ''additive'' or ''replacing'' the cell face momentum flux that is calculated using the CMS solver. When the ''replacing'' weir type is specified, the flow from all weirs associated with the cell face replaces the calculated momentum flux. If an additive weir is specified, then the final momentum flux for the cell face is calculated as the weighted sum of the weir and momentum equations fluxes:
Super-critical flow conditions occur when the tail-water elevation is sufficiently low. Under these conditions, the submergence coefficient, <math>C_{df}</math> is equal to 1.0.


The second approach treats the structure cells as other internal cells by adding the x- and y-components of the resistance force terms <math>M_x \text { and } M_y</math> induced by the weir structures in the depth-averaged momentum equations. The resistance forcing is represented by a quadratic drag law and the Manning’s (n) needs to be specified as the drag coefficient.


Where      and      are the momentum equations shallow water and weir equations,      is the total flow across the face, and the fractions      and      for the momentum equation and weir flow contributions are defined as:


The application of the ''additive'' weir type would be applicable when a weir is set in a levee or other elevated structure.  In cases where the levee is over topped the flow across the levee would be a combination of the weir flow and the flow over the levee surface.
[[File:Weirs_Figure_2.png|thumb|left|500px|Figure 2.  Curve fit to the USACE EM 1110-2-1603, plate 3-5, Section A-A data.]]
<br style="clear:both" />


==Numerical Implementation==


The total flux across the cell face will be the sum of all weirs specified for that cell face. However, only the fluxes associated with the weirs will be included in the momentum balance.
A specially designed implicit scheme is developed to couple the flow computations of the upstream and downstream of weir structures (Wu 2012).  Multiple weirs can be specified in the CMS and each weir is implemented on a line of cells (cell string), as shown in Figure 3. The model assumes the same fluxes across the upstream and downstream
interfaces of each weir cell, and the flux is calculated with the following equation that is modified from Equation (2):


When salinity or sediment transport is included in simulations with weirs, the salinity and suspended sediment will be transported.  The bedload components in sediment transport algorithms will not be transported over weirs.
{{Equation|<math>q = C_{df}C_w ^' C_{wl} \sqrt{g} h^{1.5}ds</math>|6}}


==Example Application==
where ds is the length of the face upstream or downstream of a weir cell, and C<sub>wl</sub> is a coefficient of distribution of flow discharge over the cells of each weir structure. Since <math>\Sigma q = Q</math>, the following constraint should be applied to the distribution coefficient, C<sub>wl</sub>:
[[File:Weirs_Figure_4.png|thumb|right|900px|Figure 4. CMS grid for BCS Weir Simulation.]]
As an example of weir applications in the CMS, the CMS model was applied to the simulation of flow through the Bonnet Carre Spillway (BCS), which is located along the lower Mississippi River.  The feasibility of locating a port facility along the Mississippi River at the Bonnet Carre Spillway was being investigated. The major concern was that the facility structures would interfere with the flow of flood waters from the Mississippi River through the spillway.


{{Equation|<math>\Sigma C_{wl} ds = L_w</math>|7}}


The purpose of the BCS is to divert floodwater from the Mississippi River to the Gulf of Mexico via Lake Pontchartrain. The spillway is located at River Mile 128 and was designed to pass 250,000 cfs of Mississippi River floodwater at the design stage to Lake Pontchartrain via a 5.7 mile long spillway.  The BCS will be operated, in conjunction with other area structures, to divert sufficient floodwater from the Mississippi River to prevent the discharge in the Mississippi River from exceeding 1,250,000 cfs at New Orleans.
where the summation is applied over all the cells of each weir structure. If a constant C<sub>wl</sub> is assumed, <math>C_{wl} = L_w /\Sigma ds</math>. One may also specify different values for C<sub>wl</sub> on the cells according to their locations, bottom elevations, etc. For example, a smaller value can be given to the cells near the banks, and zero for those cells where the weir is blocked or inactive.


The implicit CMS-Flow model uses the SIMPLEC algorithm to solve the continuity and
momentum equations (Wu et al. 2011). The flux (q) in Equation (6) is calculated using an implicit scheme by expanding q to a first-order Taylor series and deriving the flux and water level corrections. In the simulations of salinity or sediment transport with weirs, the salinity and suspended sediment will be transported over weir structures, but the bed load will be trapped.


The inlet structure of the BCS is a needle-controlled weir, located about a quarter of a mile from the riverbank.  The weir is designed as a concrete gravity-over-fall dam consisting of 350 bays, each 20 feet in width, separated by 2-foot wide concrete piers.  There are 176 bays in four groups, with weir crest elevations at 17.80 and 174 bays in three groups, with weir crest elevations at 15.80 ft.  When in operation, the flow over the spillway weirs is free flowing, and there is no influence from the tail-water elevations.




The 2-D CMS model domain was set to extend from the upstream gage at Reserve, which is about 8 miles upstream of the BCS, down to the Carrollton gage, which is south of New Orleans and about 27 miles downstream of the BCS.  The domain is shown in Figure 4 and includes an expanded view in the vicinity of the BCS.  The grid spacing was set to 196.8 ft (60 m).  The river levees were used to delineate the boundary since they are expected to be slightly higher than the water elevations expected in the model simulations. The grid required 16,975 cells to cover the modeling domain.


The CMS-Flow explicit solver uses a staggered grid for the basis of the numerical solution.  Weirs are implemented on the cell faces by specifying the two adjacent cells.  The order of the cell specification is not critical for the weir implementation since the algorithm implemented in the CMS will determine the flow regime and the flow direction from the specified weir crest elevation and the water elevation in the adjacent cells.  Figure 6 shows a typical CMS grid with a weir specified at a cell face.


The entrance area to the BCS was included in the model as well as a short section downstream of the spillway.  Since the flow over the BCS was the main concern in the analysis, and the flow of the weirs is super-critical (no tail-water effects), the downstream section is only needed to provide an outlet for the flow and the model configuration for this area does not impact the results of the analysis.  The weirs were assigned along a sequence of grid cells that coincide with the physical location of the BCS.
[[File:Weirs_Figure_3.png|thumb|left|400px|Figure 3.  CMS grid and designation of weirs.]]
<br style="clear:both" />


The grid extent was designed to coincide with gage locations so that measured data could be used as boundary conditions.  Flow data from the Tarbert gage was used for the upstream flow boundary condition, and stage data from the Carrolton gage was used for the downstream water elevation boundary condition.  A downstream water surface elevation for the extension of the spillway towards Lake Pontchartrain is also required, but the results of the analysis are not sensitive to the selection of this value.  The value only needs to be sufficiently lower than the weir crest elevation to allow for supercritical flow over the weirs and high enough to keep the spillway submerged.
In addition to the weir location,the user must also specify the crest elevation relative to the model datum, crest length L and the coefficient  QUOTE  .  Multiple weirs can be specified at each face and the total flow across the face is the sum of the flow calculated for each individual weir.  The momentum flux associated with the flow over the weir (and subsequently across the CMS cell face) is included in both the mass balance and the momentum balance calculations.  Also, a weir can be specified as ''additive'' or ''replacing'' the cell face momentum flux that is calculated using the CMS solver.  When the ''replacing'' weir type is specified, the flow from all weirs associated with the cell face replaces the calculated momentum flux.  If an additive weir is specified, then the final momentum flux for the cell face is calculated as the weighted sum of the weir and momentum equations fluxes:




Three scenarios were selected for the model calibration and validation.  The first two are high flow cases with the BCS closed.  Data from March 9, 2001 was used for the calibration case and recorded stage.  Flow from January 31, 2005 was used for validation of the model.  The third calibration case used data from April 22, 2008 while a major flood event occurred and for which the BCS was opened.  This case was used to validate the weir function in the CMS.  For all cases, the calibration consisted of comparing the predicted stage at the Reserve gage.  For Case 3, a comparison of the simulated and measured flow over the BCS was assessed.
Where      and      are the momentum equations shallow water and weir equations,      is the total flow across the face, and the fractions      and       for the momentum equation and weir flow contributions are defined as:
 
   
   
The representation of the weirs in the model required special processing to ensure that the total length of the BCS weir system was correctly represented since the grid cells were longer than the individual BCS bays. The BCS contains 350 bays, each with a 20 ft (6.09 m) weir.  Each bay is separated by a 2-foot thick wall, thus the total length of the spillway is 7,698 feet (when the last wall is not included).  In order to simulate the operating conditions of the spillway bays, 40 cells were identified at the approximate location of the Bonnet Carre spillway.  In order to correctly represent the total length of the BCS weirs in the model, each cell coincident with the BCS was assigned a total weir length equivalent to 8.75 bays, which is equivalent to 350 bays divided among 40 grid cells.  Thus, each cell contained 175 feet of weir crest.


The application of the ''additive'' weir type would be applicable when a weir is set in a levee or other elevated structure.  In cases where the levee is over topped the flow across the levee would be a combination of the weir flow and the flow over the levee surface.


Another characteristic of the BCS bays is their alternating weir crest elevations.  The bays are organized into seven sections.  The length of each section, number of bays and weir crest elevations are shown in Table 2.  The number of cells that were used to represent each section and the corresponding weir length are provided in the last two columns.  The spillway sections are numbered from west to east:


<br style="clear:both" />
The total flux across the cell face will be the sum of all weirs specified for that cell face. However, only the fluxes associated with the weirs will be included in the momentum balance.
'''Table 2.  BCS Weir Configuration'''
{|border="2" cellspacing="0" cellpadding="4" width="100%" align="left"
|align = "center"|Section (numbered from west to east)
|align = "center"|Number of Bays
|align = "center"|Elevation of Weirs (ft)
|align = "center"|Total BCS Weir Length in Section
|align = "center"|Number of Grid Cells used for Each Section
|align = "center"|Total Length (ft) of Weir Represented in Grid Cells
|-
|align = "center"|1
|align = "center"|44
|align = "center"|17.22
|align = "center"|880
|align = "center"|5
|align = "center"|875
|-
|align = "center"|2
|align = "center"|43
|align = "center"|15.35
|align = "center"|860
|align = "center"|5
|align = "center"|875
|-
|align = "center"|3
|align = "center"|44
|align = "center"|17.22
|align = "center"|880
|align = "center"|5
|align = "center"|875
|-
|align = "center"|4
|align = "center"|88
|align = "center"|15.35
|align = "center"|1,720
|align = "center"|10
|align = "center"|1,750
|-
|align = "center"|5
|align = "center"|44
|align = "center"|17.22
|align = "center"|880
|align = "center"|5
|align = "center"|875
|-
|align = "center"|6
|align = "center"|43
|align = "center"|15.35
|align = "center"|860
|align = "center"|5
|align = "center"|875
|-
|align = "center"|7
|align = "center"|44
|align = "center"|17.22
|align = "center"|880
|align = "center"|5
|align = "center"|875
|}<br clear="all">


For Cases 1 and 2, the weir crest elevations were set to approximately 30 feet to insure that no flow passed through the spillway.  The model calibration was obtained by globally adjusting the friction parameter (Manning<nowiki>’</nowiki>s n) until the model reproduced the measured upstream stage at the Reserve gage location.  After a few simulations; the value of 0.019 was found to yield the best results.  The velocity patterns in the vicinity of the spillway for Case 1 are shown in Figure 5.  The model was then configured for the validation case (Case 2) to verify whether the model could reproduce good results for different stage and flow conditions.  The results for these two cases are shown in Table 3.
When salinity or sediment transport is included in simulations with weirs, the salinity and suspended sediment will be transported.  The bedload components in sediment transport algorithms will not be transported over weirs.


'''Table 3.  Model Calibration and Validation Results.'''
{|border="2" cellspacing="0" cellpadding="4" width="82%" align="left"
|align = "center"|'''Case ID'''
|align = "center"|'''Type'''
|align = "center"|'''Carrollton Stage (ft) (downstream boundary condition)'''
|align = "center"|'''Tarbert Flow (cfs) (Upstream flow boundary)'''
|align = "center"|'''Expected Reserve Stage (ft)'''
|align = "center"|'''Simulated Reserve Stage (ft)'''
|align = "center"|'''Percent Error'''
|-
|1
|Calibration
|13.9
|1,097,818
|19.7
|20.2
|2.5
|-
|2
|Validation
|15.5
|1,185,445
|22.0
|22.7
|3.2
|-
|3
|Validation
|16.7
|1,465,000
|23.7
|23.2
|2.1
|}<br clear="all">
[[File:Weirs_Figure_5.png|thumb|left|600px|Figure 5.  CMS simulation velocity patterns for Case 1.]]
<br style="clear:both" />
The final validation was completed for Case 3, which represents the flood event of 2008, and was used to calibrate the coefficients in the CMS weir representations.  The 2008 flood report (URS, 2009), which documents the 2008 flood event, provides information on which bays of the BCS were open and the total flow through each bay.  The total flow was estimated to be 167,000 cfs and 160 bays were opened.  The total flow through the spillway in the simulation was 169,221 cfs using a weir coefficient of 0.57 and the stage results are shown in Table 3.  The simulated velocity patterns for the flow through the spillway are shown in Figure 6.  The effect on the staggered open bays is evident in the flow patterns.
[[File:Weirs_Figure_6.png|thumb|left|600px|Figure 6.  CMS simulation velocity patterns for Case 3.]]
<br style="clear:both" />


==Additional Information==
==Additional Information==
Line 219: Line 96:
==References==
==References==
*Buttolph, A. M., C. W. Reed, N. C. Kraus, N. Ono, M. Larson, B. Camenen, H. Hanson, T. Wamsley, and A. . Zundel, A. K. 2006. Two-dimensional depth-averaged circulation model CMS-M2D: Version 3.0, Report 2, sediment transport and morphology change. Coastal and Hydraulics Laboratory Technical Report ERDC/CHL-TR-06-7. Vicksburg, MS: U.S. Army Engineer Research and Development Center.
*Buttolph, A. M., C. W. Reed, N. C. Kraus, N. Ono, M. Larson, B. Camenen, H. Hanson, T. Wamsley, and A. . Zundel, A. K. 2006. Two-dimensional depth-averaged circulation model CMS-M2D: Version 3.0, Report 2, sediment transport and morphology change. Coastal and Hydraulics Laboratory Technical Report ERDC/CHL-TR-06-7. Vicksburg, MS: U.S. Army Engineer Research and Development Center.
*Hydrological Engineering Center (HEC). 2010. HEC-RAS River Analysis System, Hydraulic Reference Manual, Version 4.1, Davis, California: HEC, US Army Corps of Engineers.


*Militello, A., Reed, C.W., Zundel, A.K., and Kraus, N.C.  2004.  Two-Dimensional Depth-Averaged Circulation Model M2D: Version 2.0, Report 1, Technical Documentation and User<nowiki>’</nowiki>s Guide, ERDC/CHL TR-04-2, U.S. Army Research and Development Center, Coastal and Hydraulics Laboratory, Vicksburg, MS.
*Militello, A., Reed, C.W., Zundel, A.K., and Kraus, N.C.  2004.  Two-Dimensional Depth-Averaged Circulation Model M2D: Version 2.0, Report 1, Technical Documentation and User<nowiki>’</nowiki>s Guide, ERDC/CHL TR-04-2, U.S. Army Research and Development Center, Coastal and Hydraulics Laboratory, Vicksburg, MS.
*Reed, C. W., and A. Sanchez. 2011. Representation of rubble mound structures in the Coastal Modeling System.  CIRP Wiki, http://cirp.usace.army.mil/wiki/References#Structures.


*URS. 2009. Hydraulic Modeling of Proposed Container Facility Along Mississippi River at Bonnet Carre<nowiki>’</nowiki> Spillway. URS Corporation, Tallahassee, FL.
*URS. 2009. Hydraulic Modeling of Proposed Container Facility Along Mississippi River at Bonnet Carre<nowiki>’</nowiki> Spillway. URS Corporation, Tallahassee, FL.


*Villemonte, J.R (December 25,1947). "Submerged Weir Discharge Studies." Engineering News Record, p. 866-869.
*Villemonte, J.R (December 25,1947). "Submerged Weir Discharge Studies." Engineering News Record, p. 866-869.
*Wu, W., A. Sanchez, and M. Zhang. 2011. An implicit 2D depth-averaged finite-volume model of flow and sediment
transport in coastal waters, ICCE 2010. Vicksburg, MS: US Army Engineer Research and Development Center.
*Wu, W. 2012. Implementation of structures in the implicit CMS2D model. An Interim Report to Coastal Inlets Research Program. Vicksburg, MS: US Army Engineer Research and Development Center.


-----
-----

Latest revision as of 17:08, 25 February 2015


Representation of Weirs in the CMS

By Christopher Reed and Alejandro Sánchez

Last Date Modified: September 17, 2010

Introduction

Weirs are a common coastal engineering structure used to control flow and can affect sediment transport. They are typically used in weir jetties or in wetlands to control discharges, provide flood control, act as salinity barriers and optimally distribute freshwater to manage salinity regimes and sedimentation rates and deposition patterns. Since these structures are a significant component of hydrodynamic and sediment transport controls in the coastal zone, it is important that the CMS simulate their effects. The simulation of weirs is based on the standard weir equation for either sharp-crested or broad-crested weirs, with a foundation in Bernoulli’s equation. The implementation of weirs in the CMS is validated in two applications on the lower Mississippi River. The weirs are applied in the simulation of flow over the Bonne Carrie spillway north of New Orleans.

Formulation

Two approaches are developed to implement weir structures in the CMS. In the first approach the standard weir equation for a rectangular crosssection is introduced in the model as follows (HEC 2010):

  (1)

where Q is the flow rate over the weir crest, is the weir coefficient, is the weir crest length, is the upstream water depth above the crest, and is the submergence correction factor (also referred to as the drowned flow reduction factor). A definition schematic for both the free flow and submerged flow conditions is provided in Figure 1.

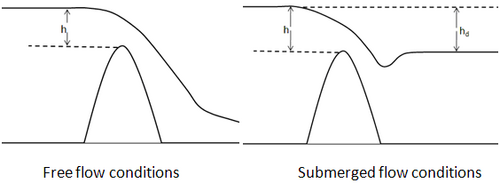
Figure 1. Schematic showing weir flow conditions.


To obtain a non-dimensional weir coefficient, Equation (1) can be re-written as (Reed and Sanchez 2011)

  (2)

where . Ranges for were suggested in HEC (2010). For a sharp-crested weir, it is between 0.55 and 0.58, and a broad-crested weir between 0.46 and 0.55.

The submergence coefficient (Cdf) is determined using different methods. For a sharp-crested weir, the Villemonte formula is used,

  (3)

where and are the upstream and downstream water levels above the weir crest elevation, respectively. For a broad-crested weir,  is calculated as

  (4)

For a spillway-type weir, is obtained by fitting a curve to data (Reed and Sanchez 2011),

  (5)

Super-critical flow conditions occur when the tail-water elevation is sufficiently low. Under these conditions, the submergence coefficient, is equal to 1.0.

The second approach treats the structure cells as other internal cells by adding the x- and y-components of the resistance force terms induced by the weir structures in the depth-averaged momentum equations. The resistance forcing is represented by a quadratic drag law and the Manning’s (n) needs to be specified as the drag coefficient.


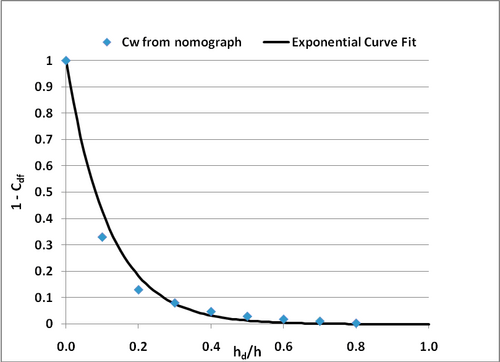
Figure 2. Curve fit to the USACE EM 1110-2-1603, plate 3-5, Section A-A data.


Numerical Implementation

A specially designed implicit scheme is developed to couple the flow computations of the upstream and downstream of weir structures (Wu 2012). Multiple weirs can be specified in the CMS and each weir is implemented on a line of cells (cell string), as shown in Figure 3. The model assumes the same fluxes across the upstream and downstream interfaces of each weir cell, and the flux is calculated with the following equation that is modified from Equation (2):

  (6)

where ds is the length of the face upstream or downstream of a weir cell, and Cwl is a coefficient of distribution of flow discharge over the cells of each weir structure. Since , the following constraint should be applied to the distribution coefficient, Cwl:

  (7)

where the summation is applied over all the cells of each weir structure. If a constant Cwl is assumed, . One may also specify different values for Cwl on the cells according to their locations, bottom elevations, etc. For example, a smaller value can be given to the cells near the banks, and zero for those cells where the weir is blocked or inactive.

The implicit CMS-Flow model uses the SIMPLEC algorithm to solve the continuity and momentum equations (Wu et al. 2011). The flux (q) in Equation (6) is calculated using an implicit scheme by expanding q to a first-order Taylor series and deriving the flux and water level corrections. In the simulations of salinity or sediment transport with weirs, the salinity and suspended sediment will be transported over weir structures, but the bed load will be trapped.



The CMS-Flow explicit solver uses a staggered grid for the basis of the numerical solution. Weirs are implemented on the cell faces by specifying the two adjacent cells. The order of the cell specification is not critical for the weir implementation since the algorithm implemented in the CMS will determine the flow regime and the flow direction from the specified weir crest elevation and the water elevation in the adjacent cells. Figure 6 shows a typical CMS grid with a weir specified at a cell face.

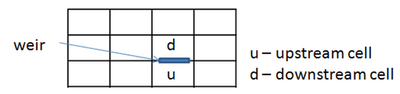
Figure 3. CMS grid and designation of weirs.


In addition to the weir location,the user must also specify the crest elevation relative to the model datum, crest length L and the coefficient QUOTE . Multiple weirs can be specified at each face and the total flow across the face is the sum of the flow calculated for each individual weir. The momentum flux associated with the flow over the weir (and subsequently across the CMS cell face) is included in both the mass balance and the momentum balance calculations. Also, a weir can be specified as additive or replacing the cell face momentum flux that is calculated using the CMS solver. When the replacing weir type is specified, the flow from all weirs associated with the cell face replaces the calculated momentum flux. If an additive weir is specified, then the final momentum flux for the cell face is calculated as the weighted sum of the weir and momentum equations fluxes:


Where and are the momentum equations shallow water and weir equations, is the total flow across the face, and the fractions and for the momentum equation and weir flow contributions are defined as:


The application of the additive weir type would be applicable when a weir is set in a levee or other elevated structure. In cases where the levee is over topped the flow across the levee would be a combination of the weir flow and the flow over the levee surface.


The total flux across the cell face will be the sum of all weirs specified for that cell face. However, only the fluxes associated with the weirs will be included in the momentum balance.

When salinity or sediment transport is included in simulations with weirs, the salinity and suspended sediment will be transported. The bedload components in sediment transport algorithms will not be transported over weirs.


Additional Information

This wiki technical note was prepared and funded under the Coastal Inlets Research Program (CIRP) being conducted at the U.S. Army Engineer Research and Development Center, Costal and Hydraulics Laboratory. Questions about this technical note can be addressed to to Dr. Christopher W. Reed (Chris_Reed@URSCorp.com) of URS Corporation, the CIRP Program Manager, Dr. Julie D. Rosati (Julie.D.Rosati@usace.army.mil), the assistant Program Manager, Dr. Nicholas C. Kraus (Nicholas.C.Kraus@usace.army.mil).

References

  • Buttolph, A. M., C. W. Reed, N. C. Kraus, N. Ono, M. Larson, B. Camenen, H. Hanson, T. Wamsley, and A. . Zundel, A. K. 2006. Two-dimensional depth-averaged circulation model CMS-M2D: Version 3.0, Report 2, sediment transport and morphology change. Coastal and Hydraulics Laboratory Technical Report ERDC/CHL-TR-06-7. Vicksburg, MS: U.S. Army Engineer Research and Development Center.
  • Hydrological Engineering Center (HEC). 2010. HEC-RAS River Analysis System, Hydraulic Reference Manual, Version 4.1, Davis, California: HEC, US Army Corps of Engineers.
  • Militello, A., Reed, C.W., Zundel, A.K., and Kraus, N.C. 2004. Two-Dimensional Depth-Averaged Circulation Model M2D: Version 2.0, Report 1, Technical Documentation and User’s Guide, ERDC/CHL TR-04-2, U.S. Army Research and Development Center, Coastal and Hydraulics Laboratory, Vicksburg, MS.
  • URS. 2009. Hydraulic Modeling of Proposed Container Facility Along Mississippi River at Bonnet Carre’ Spillway. URS Corporation, Tallahassee, FL.
  • Villemonte, J.R (December 25,1947). "Submerged Weir Discharge Studies." Engineering News Record, p. 866-869.
  • Wu, W., A. Sanchez, and M. Zhang. 2011. An implicit 2D depth-averaged finite-volume model of flow and sediment

transport in coastal waters, ICCE 2010. Vicksburg, MS: US Army Engineer Research and Development Center.

  • Wu, W. 2012. Implementation of structures in the implicit CMS2D model. An Interim Report to Coastal Inlets Research Program. Vicksburg, MS: US Army Engineer Research and Development Center.

Documentation Portal

Retrieved from "https://cirpwiki.info/index.php?title=Weirs&oldid=11610"