Circular Basin: Difference between revisions
No edit summary |
|||
| (13 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
=Problem= | =Problem= | ||
Dupont (2001) presented an analytical solution for a closed circular domain on an f-plane with a linear bottom friction. The governing equations are | Dupont (2001) presented an analytical solution for a closed circular domain on an f-plane with a linear bottom friction. The governing equations are | ||
{{Equation|<math> | |||
\frac{\partial H U}{\partial x} + \frac{\partial H V}{\partial y} = 0 | |||
</math>|1}} | |||
{{Equation|<math> | |||
-f_c V + g \frac{\partial \eta}{\partial x} = \kappa U + \frac{W y}{R H} | |||
</math>|2}} | |||
{{Equation|<math> | |||
f_c U + g \frac{\partial \eta}{\partial y} = \kappa V | |||
</math>|3}} | |||
where <math>U</math> and <math>V</math> are the depth-averaged current velocities in the <math>x</math> and <math>y</math> directions respectively, <math>g</math> is the gravitational constant, <math>\eta</math> is the water surface elevation with respect to mean sea level, <math>\kappa</math> is a linear bottom friction coefficient, <math>R</math> is the radius of the domain, <math>H</math> is the water depth, and <math>W</math> is a constant equal to the gradient of the wind forcing. | where <math>U</math> and <math>V</math> are the depth-averaged current velocities in the <math>x</math> and <math>y</math> directions respectively, <math>g</math> is the gravitational constant, <math>\eta</math> is the water surface elevation with respect to mean sea level, <math>\kappa</math> is a linear bottom friction coefficient, <math>R</math> is the radius of the domain, <math>H</math> is the water depth, and <math>W</math> is a constant equal to the gradient of the wind forcing. | ||
| Line 11: | Line 19: | ||
=Solution= | =Solution= | ||
The analytical solution for water surface elevation solution is given by | The analytical solution for water surface elevation solution is given by | ||
{{Equation| <math> \eta = | {{Equation|<math> | ||
\begin{cases} | \eta = | ||
\frac{W{{r}^{2}}\sin 2\theta }{4gHR}, & \mbox{if } f_c=0 \\ | \begin{cases} | ||
\frac{W{{f}_{c}}}{RgH\kappa }\left[ \frac{{{R}^{2}}}{8}+\frac{{{r}^{2}}}{4}\left( \frac{\kappa }{{{f}_{c}}}\sin 2\theta -1 \right) \right], & \mbox{if } f_c \ne0 \\ | \frac{W{{r}^{2}}\sin 2\theta }{4gHR}, & \mbox{if } f_c=0 \\ | ||
\end{cases} | \frac{W{{f}_{c}}}{RgH\kappa }\left[ \frac{{{R}^{2}}}{8}+\frac{{{r}^{2}}}{4}\left( \frac{\kappa }{{{f}_{c}}}\sin 2\theta -1 \right) \right], & \mbox{if } f_c \ne0 \\ | ||
\end{cases} | |||
</math>|4}} | |||
The current velocities are independent of the Coriolis parameter and are given by | The current velocities are independent of the Coriolis parameter and are given by | ||
{{Equation| <math> U = \frac{W y }{2 R H \kappa} </math> | | {{Equation|<math> | ||
{{Equation| <math> V = -\frac{W x }{2 R H \kappa} </math> | | U = \frac{W y }{2 R H \kappa} | ||
</math>|5}} | |||
{{Equation|<math> | |||
V = -\frac{W x }{2 R H \kappa} | |||
</math>|6}} | |||
= Setup = | = Setup = | ||
| Line 25: | Line 40: | ||
The model is run to steady state from zero current and water level initial conditions with <math> W = 10^-4 \text{m}^2 \text{s}^{-2} </math>, <math> \kappa = 10^{-3} \text{s}^{-1} </math> , and <math> f_c = 0</math>. Table 1 shows the general settings used for CMS-Flow. Figure 1 shows the computational grid with 5 levels of refinement from 2000 m to 125 m. | The model is run to steady state from zero current and water level initial conditions with <math> W = 10^-4 \text{m}^2 \text{s}^{-2} </math>, <math> \kappa = 10^{-3} \text{s}^{-1} </math> , and <math> f_c = 0</math>. Table 1 shows the general settings used for CMS-Flow. Figure 1 shows the computational grid with 5 levels of refinement from 2000 m to 125 m. | ||
<br style="clear:both" /> | |||
'''Table 1. General Settings for Wind-driven flow in a circular basin''' | '''Table 1. General Settings for Wind-driven flow in a circular basin''' | ||
{|border="1" | {|border="1" | ||
| Line 36: | Line 51: | ||
|Ramp Period || 24 hrs | |Ramp Period || 24 hrs | ||
|- | |- | ||
|Initial Water Depth || | |Initial Water Depth || 100 m | ||
|- | |- | ||
|Mixing Terms || Off | |Mixing Terms || Off | ||
| Line 47: | Line 62: | ||
<br style="clear:both" /> | <br style="clear:both" /> | ||
= Results = | = Results = | ||
[[Image:CB3_Analytical_No_Coriolis_V4.png|thumb|left| | == No Coriolis == | ||
[[Image:CB3_Analytical_No_Coriolis_V4.png|thumb|left|600px| Figure 1. Analytical current velocities and water levels for the case without Coriolis.]] | |||
[[Image:CB3_Calculated_No_Coriolis_V5.png|thumb|right|600px| Figure 2. Calculated current velocities and water levels for the case without Coriolis.]] | |||
<br style="clear:both" /> | |||
'''Table 2. Goodness of fit statistics for the current velocity and water level.''' | |||
{|border="1" | |||
|'''Variable''' ||'''NRMSE, %'''||'''NMAE, %'''||'''R^2'''||'''Bias''' | |||
|- | |||
|U-Velocity || 2.52 || 0.37 || 0.999 || -8.5e-8 m/s | |||
|- | |||
|V-Velocity || 2.53 || 0.38 || 0.999 || 7.26e-8 m/s | |||
|- | |||
|Water Level|| 0.03 || 0.02 || 0.999 || -3.5e-7 m | |||
|} | |||
* For a definition of the goodness of fit statistics see [[Statistics | Goodness of fit statistics]]. | |||
<br style="clear:both" /> | <br style="clear:both" /> | ||
Table | == With Coriolis == | ||
[[Image:CB3_Analytical_Coriolis_V4.png|thumb|left|600px| Figure 3. Analytical current velocities and water levels for the case with Coriolis.]] | |||
[[Image:CB3_Calculated_Coriolis_V5.png|thumb|right|600px| Figure 4. Calculated current velocities and water levels for the case with Coriolis.]] | |||
<br style="clear:both" /> | |||
'''Table 3. Goodness of fit statistics for the current velocity and water level.''' | |||
{|border="1" | {|border="1" | ||
|'''Variable''' ||'''RRMSE, %'''||'''RMAE, %'''||'''R^2'''||'''Bias''' | |'''Variable''' ||'''RRMSE, %'''||'''RMAE, %'''||'''R^2'''||'''Bias''' | ||
|- | |- | ||
|U-Velocity || | |U-Velocity || 2.53 || 0.37 || 0.999 || -8.5e-8 m/s | ||
|- | |- | ||
|V-Velocity || | |V-Velocity || 2.56 || 0.37 || 0.999 || 6.5e-8 m/s | ||
|- | |- | ||
|Water Level|| 0. | |Water Level|| 0.03 || 0.02 || 0.999 || -3.0e-7 m | ||
|} | |} | ||
<br style="clear:both" /> | |||
= References = | = References = | ||
Latest revision as of 20:07, 18 April 2013
UNDER CONSTRUCTION
Problem
Dupont (2001) presented an analytical solution for a closed circular domain on an f-plane with a linear bottom friction. The governing equations are
| (1) |
| (2) |
| (3) |
where and are the depth-averaged current velocities in the and directions respectively, is the gravitational constant, is the water surface elevation with respect to mean sea level, is a linear bottom friction coefficient, is the radius of the domain, is the water depth, and is a constant equal to the gradient of the wind forcing.
Solution
The analytical solution for water surface elevation solution is given by
| (4) |
The current velocities are independent of the Coriolis parameter and are given by
| (5) |
| (6) |
Setup

The model is run to steady state from zero current and water level initial conditions with , , and . Table 1 shows the general settings used for CMS-Flow. Figure 1 shows the computational grid with 5 levels of refinement from 2000 m to 125 m.
Table 1. General Settings for Wind-driven flow in a circular basin
| Parameter | Value |
| Time step | 3600 s |
| Simulation Duration | 72 hrs |
| Ramp Period | 24 hrs |
| Initial Water Depth | 100 m |
| Mixing Terms | Off |
| Wall Friction | Off |
| Linear Bottom Friction Coefficient | 0.001 |
Results
No Coriolis
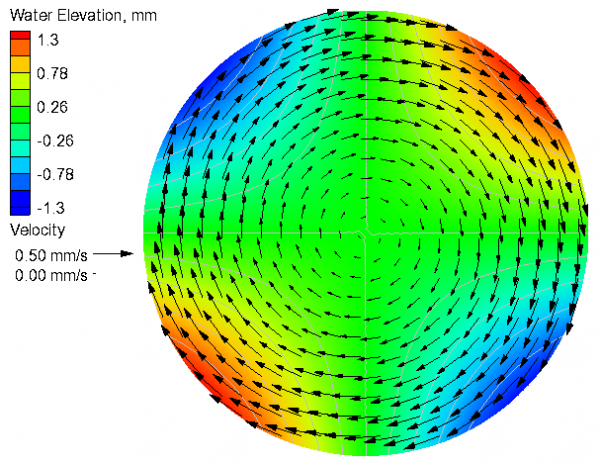
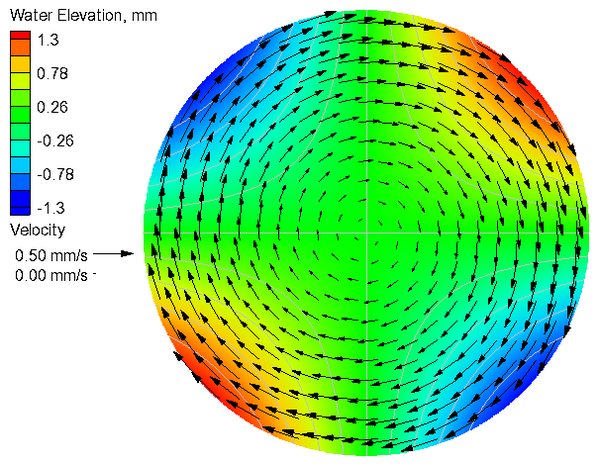
Table 2. Goodness of fit statistics for the current velocity and water level.
| Variable | NRMSE, % | NMAE, % | R^2 | Bias |
| U-Velocity | 2.52 | 0.37 | 0.999 | -8.5e-8 m/s |
| V-Velocity | 2.53 | 0.38 | 0.999 | 7.26e-8 m/s |
| Water Level | 0.03 | 0.02 | 0.999 | -3.5e-7 m |
- For a definition of the goodness of fit statistics see Goodness of fit statistics.
With Coriolis
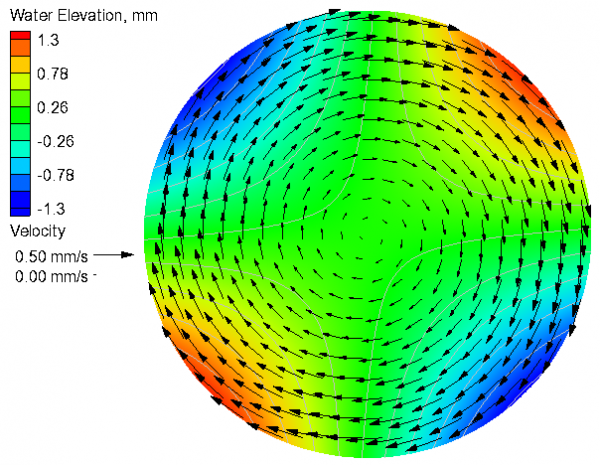
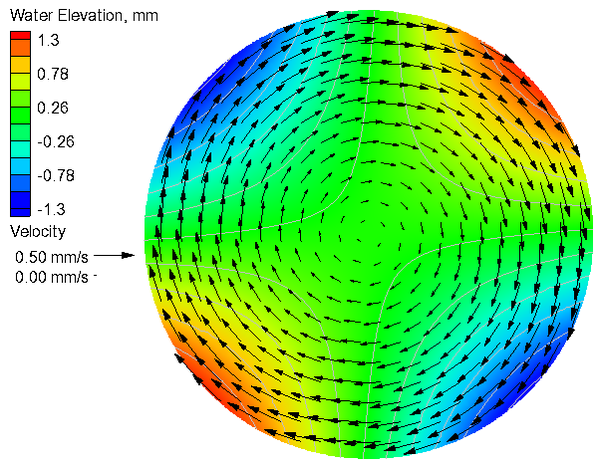
Table 3. Goodness of fit statistics for the current velocity and water level.
| Variable | RRMSE, % | RMAE, % | R^2 | Bias |
| U-Velocity | 2.53 | 0.37 | 0.999 | -8.5e-8 m/s |
| V-Velocity | 2.56 | 0.37 | 0.999 | 6.5e-8 m/s |
| Water Level | 0.03 | 0.02 | 0.999 | -3.0e-7 m |
References
- Dupont, F., 2001. Comparison of numerical methods for modelling ocean circulation in basins with irregular coasts. Ph.D. thesis, McGill University, Montreal.