CMS-Flow:Non-equilibrium Sediment Transport: Difference between revisions
No edit summary |
|||
| (155 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
''' | ''' UNDER CONSTRUCTION''' | ||
''written by Alejandro Sanchez'' | |||
Last date modified: December 8, 2010 | |||
= | = Total-load Transport Equation = | ||
The single-sized sediment transport model described in Sánchez and Wu (2011a) was extended to multiple-sized sediments within CMS by Sánchez and Wu (2011b). In this model, the sediment transport is separated into current- and wave-related transports. The transport due to currents includes the stirring effect of waves, and the wave-related transport includes the transport due to asymmetric oscillatory wave motion as well as steady contributions by Stokes drift, surface roller, and undertow. The current-related bed and suspended transports are combined into a single total-load transport equation, thus reducing the computational costs and simplifying the bed change computation. The 2DH transport equation for the current-related total load is | |||
{{Equation| | |||
<math> | |||
\frac{\partial}{\partial t} \biggl( \frac{ h C_{tk} }{\beta _{tk}} \biggr) + \frac{\partial (U_j h C_{tk})}{\partial x_j} = \frac{\partial }{\partial x_j} \biggl[ \nu _s h \frac{\partial (r_{sk} C_{tk})}{\partial x_j} \biggr] + \alpha _t \omega _{sk} (C_{t*k} - C_{tk}) | |||
</math>|1}} | |||
for ''j''= 1,2; k=1,2...,N, where ''N'' is the number of sediment size classes and | |||
:<math>C_{tk}</math> = actual depth-averaged total-load sediment concentration [kg/m<sup>3</sup>] for size class ''k'' defined as <math>C_{tk} = q_{tk}/(Uh)</math> in which <math>q_{tk}</math> is the total-load mass transport | |||
= | :<math>C_{tk*}</math> = equilibrium depth-averaged total-load sediment concentration [kg/m<sup>3</sup>] for size class ''k'' and described in the equilibrium concentration and transport rates section | ||
:<math>\beta_{tk}</math> = total-load correction factor described in the Total-Load Correction Factor section [-] | |||
:<math>r_{sk}</math> = fraction of suspended load in total load for size class k described in fraction of suspended sediments section [-] | |||
= | :<math>v_s</math> = horizontal sediment mixing coefficient described in the horizontal sediment mixing coefficient section [m<sup>2</sup>/s] | ||
:<math>\alpha_t</math> = total-load adaptation coefficient described in the adaptation coefficient section [-] | |||
:<math>\omega_{sk}</math> = sediment fall velocity [m/s]. | |||
= | In the above equation, the first term represents the temporal variation of <math>C_{tk}</math>; the second term represents the horizontal advection; the third term represents the horizontal diffusion and dispersion of suspended sediments; and the last term represents the erosion and deposition. The equation may be applied to single-sized sediment transport by using a single sediment size class (i.e., N = 1). The bed composition, however, does not vary when using a single sediment size class. The units of sediment concentration used here are kg/m<sup>3</sup> rather than dimensionless volume concentrations in order to avoid numerical precision errors at low concentrations. | ||
In the above equations, it is assumed that the wave flux velocity is not included in the momentum equations. If the wave flux velocity is included, then the total flux velocity ''(V)'' should be used instead of the depth-averaged current velocity ''(U)''. The reason for this is because without a wave-induced sediment transport to counter the offshore directed transport due to the undertow, the model would predict excessive movement of sediment offshore. | |||
= Fraction of Suspended Sediment = | |||
In order to solve the system of equations for sediment transport implicitly, the fraction of suspended sediment must be determined explicitly. This is done by assuming | |||
= | {{Equation| | ||
<math>r_{sk} = \frac{q_{sk}}{q_{tk}} \simeq \frac{q_{sk*}}{q_{tk*}} | |||
</math>|2}} | |||
where <math>q_{sk} \text{and } q_{tk}</math> are the actual suspended- and total-load transport rates and <math>q_{sk*} \text{and } q_{tk*}</math> are the equilibrium suspended- and total-load transport rates. | |||
=Adaptation Coefficient= | |||
The total-load adaptation coefficient <math>(\alpha_t )</math> is an important parameter in the sediment transport model. There are many variations of this parameter in literature (Lin 1984; Gallappatti and Vreugdenhil 1985; and Armanini and di Silvio 1986). CMS uses a total-load adaptation coefficient <math>(\alpha_t )</math> that is related to the total-load adaptation length (L<sub>t</sub> ) and time (T<sub>t</sub>) by | |||
{{Equation| | |||
<math>L_t = \frac{Uh}{\alpha_t \omega_s} = UT_t</math> | |||
|3}} | |||
where: | |||
:<math>\omega_s</math> = sediment fall velocity corresponding to the transport grain size for single-sized sediment transport or the median grain size for multiple-sized sediment transport [m/s] | |||
= | :U = depth-averaged current velocity [m/s] | ||
:h = water depth [m]. | |||
The adaptation length or time is a characteristic distance or time for sediment to adjust from non-equilibrium to equilibrium transport. Because the total load is a combination of the bed and suspended loads, the associated adaptation length may be calculated as <math> L_t = r_s L_s + (1 - r_s)L_b \text{ or } L_t = \text{ max }(L_s, L_b ), \text{where } L_s \text{and } L_b</math> are the suspended- and bed-load adaptation lengths. The symbol <math>L_s</math> is defined as | |||
== | {{Equation| | ||
<math>L_s = \frac {Uh}{\alpha \omega_s} = UT_s | |||
</math>|4}} | |||
in which <math>\alpha \text{ and } T_s</math> are the adaptation coefficient lengths for suspended load. The adaptation coefficient ''<math>(\alpha )</math>'' can be calculated either empirically or based on analytical solutions to the pure vertical convection-diffusion equation of suspended sediment. One example of an empirical formula is that proposed by Lin (1984): | |||
{{Equation| | |||
<math>\alpha = 3.25 + 0.55 \ ln \big(\frac{\omega_s}{\kappa u_*}\big) </math>|5}} | |||
where u<sub>*</sub> is the bed shear stress, and <math>\kappa</math> is the von Karman constant. Armanini and di Silvio (1986) proposed an analytical equation: | |||
{{Equation|<math>\frac{1}{a} = \frac{\delta}{h} + \left(1 - \frac{\delta}{h}\right)\exp \left[-1.5\left(\frac{\delta}{h}\right)^{-1/6} \frac{\omega_s}{u_*} \right]</math>|6}} | |||
where <math>\delta</math> is the thickness of the bottom layer defined by <math>\delta = 33 z_0 \text { and } z_0</math> is the zero-velocity distance from the bed. Gallappatti (1983) proposed the following equation to determine the suspended-load adaptation time: | |||
{{Equation|<math>T_s = \frac{h}{u_*}exp | |||
\left[\begin{align}&(1.57 - 20.12u_r)\omega_* ^3 + (326.832u_r ^{2.2047} - 0.2)\omega_* ^2\\& +(0.1385 \ ln \ u_r - 6.4061)\omega_* + (0.5467u_r - 2.1963)\end{align}\right]</math>|7}} | |||
== | where u<sub>*</sub> is the current related bottom shear velocity, <math>u_r = u_*/U, \text{ and } \omega_* = \omega_s /u_*</math>. | ||
The bed-load adaptation length (L<sub>b</sub>) is generally related to the dimension of bed forms such as sand dunes. Large bed forms are generally proportional to the water depth, and, therefore, the bed-load adaptation length can be estimated as L<sub>b</sub> = a<sub>b</sub>h in which a<sub>b</sub> is an empirical coefficient on the order of 5-10. Although limited guidance exists on methods to estimate L<sub>b</sub>, the determination of L<sub>b</sub> is still empirical and in the developmental stage. For a detailed discussion of the adaptation length, the reader is referred to Wu (2007). In general, it is recommended that the adaptation length be calibrated with field data in order to achieve the best and most reliable results. | |||
= Total-load correction factor = | |||
The total-load correction factor (β<sub>tk</sub>) accounts for the vertical distribution of the suspended sediment concentration and velocity profiles as well as the fact that bed load travels at a slower velocity than the depth-averaged current velocity (Figure 1) (Wu 2007). By definition, β<sub>tk</sub> is the ratio of the depth-averaged total-load and flow velocities. | |||
[[File:fig_2_3.png]]<br> | |||
'''Figure 1. Schematic of sediment and current vertical profiles.''' | |||
In a combined bed-load and suspended-load model, the correction factor is given by | |||
{{Equation|<math>\beta_{tk} = \frac{1}{r_{sk} / \beta_{sk} + (1-r_{sk})U/u_{bk}} </math>|8}} | |||
where u<sub>bk</sub> is the bed-load velocity, and β<sub>sk</sub> is the suspended-load correction factor and is defined as the ratio of the depth-averaged suspended sediment and flow velocities. Since most sediment is transported near the bed, both the total- and suspended-load correction factors (β<sub>tk</sub> and β<sub>sk</sub>) are usually less than 1 and typically in the range of 0.3 and 0.7, respectively. By assuming logarithmic current velocity and exponential suspended sediment concentration profiles, an explicit expression for the suspended-load correction factor (β<sub>sk</sub>) may be obtained as (Sánchez and Wu 2011b) | |||
{{Equation|<math> | |||
\beta_{sk} = \frac{\int_{z_b + a}^{\overline{\eta}}uc_k dz}{U\int_{z_b + a}^{\overline{\eta}}c_k dz} = | |||
\frac{E_1(\phi_k A) - E_1 (\phi_k) + ln(A/Z)e^{-\phi_k A} - ln(1/Z)e^{-\phi_k}}{e^{-\phi_k A}[ln(1/Z)-1][1-e^{-\phi_k(1-A)}]}</math>|9}} | |||
where: | |||
<math>\phi_k = \omega_{sk}h/\epsilon_k [-]</math> | |||
A = a/h [-] | |||
Z = z<sub>a</sub>/h [-] | |||
<math>\epsilon_k</math> = vertical mixing coefficient [m<sup>2</sup>/s] | |||
a = reference height near the bed for the suspended load [m] | |||
z<sub>a</sub> = apparent roughness length [m] | |||
<math>E_1 (x) = \int_x ^\infty \frac{e^{-t}}{t} dt</math> (exponential integral). | |||
The equation can be further simplified by assuming that the reference height is proportional to the apparent roughness length (e.g., a = 30z<sub>z</sub>) so that <math>\beta_{sk} = \beta_{sk}(Z,\phi_k)</math>. Figure 2 shows a comparison of the suspended-load correction factor based on the logarithmic velocity with exponential and Rouse suspended sediment concentration profiles. Both cases show similar behavior for the suspended-load correction factor (<math>\beta_{sk}</math>). For fine sediments (small fall velocity), <math>\beta_{sk}</math> is close to 1.0 and experiences smaller influences by the bottom roughness, while for course sediments, <math>\beta_{sk}</math>can be as low as 0.5 and is largely influenced by the bottom roughness. This is to be expected since course sediments are transported more closely to the bottom, compared to fine sediments. | |||
[[File:fig_2_4.png|400px]] | |||
<br> | |||
'''Figure 2. Suspended load correction factors based on the logarithmic velocity profile and (a) exponential and (b) Rouse suspended sediment profile. The Rouse number is <math>r = \omega_s /(\kappa u_* )</math>''' | |||
The bed-load velocity (u<sub>bk</sub>) in Equation 8 is calculated using the van Rijn (1984a) formula with re-calibrated coefficients from Wu et al. (2006): | |||
{{Equation|<math> | |||
u_{bk} = 1.64 \left(\frac{\tau_b ^'}{\tau_{crk}} - 1 \right)^{0.5} \sqrt{(s-1)gd_k} | |||
</math>|10}} | |||
where: | |||
s = specific gravity [-] | |||
g = gravitational constant (~9.81 m/s<sup>2</sup>) | |||
d<sub>k</sub> = characteristic grain diameter for the k<sup>th</sup> size class [m] | |||
<math>\tau_b ^' = (n^'/n)^{3/2}\tau_b</math> = grain-related bed shear stress [Pa] | |||
<math>n^' = d_{50}^{1/6}/20 \ </math> = grain-related Manning’s roughness coefficient [s/m<sup>1/3</sup>] | |||
<math>\tau_{crk}</math> = critical bed shear stress for the k<sup>th</sup> size class [Pa]. | |||
= Bed Change Equation = | |||
The change in the water depth is calculated by | |||
{{Equation|<math> | |||
\rho_s (1 - p'_m) \biggl( \frac{\partial z_b}{\partial t} \biggr)_k = \alpha _t \omega _{sk} (C_{tk} - C_{tk*}) + \frac{\partial }{\partial x_j} \biggl[ D_s q_{bk} \frac{\partial z_b}{\partial x_j} \biggr]</math>|11}} | |||
where: | |||
z<sub>b</sub> = bed elevation with respect to the vertical datum [m] | |||
p<sub>m</sub><sup>'</sup> = bed porosity [-] | |||
<math>\rho_s</math> = sediment (material) density (~2650 kg/m<sup>3</sup> for quartz sediment) | |||
D<sub>s</sub> = empirical bed-slope coefficient (constant) [-] | |||
<math>q_{bk} = hUC_{tk}(1-r_{sk})</math> is the bed-load mass transport rate magnitude [kg/m/s]. | |||
The first term on the right-hand side of the above equation represents the bed change due to sediment exchange near the bed. The last term accounts for the effect of the bed slope on bed-load transport. The bed-slope coefficient (D<sub>s</sub>) is usually about 0.1 to 3.0. For a detailed derivation of the above equation, the reader is referred to Sanchez and Wu (2011a). The total bed change is calculated as the sum of the bed changes for all size classes: | |||
{{Equation|<math> | |||
\frac{\partial z_b}{\partial t} = \sum_k \left(\frac{\partial z_b}{\partial t} \right)_k | |||
</math>|12}} | |||
= Bed Sorting and Gradation (nonuniform sediments) = | |||
When simulating nonuniform sediments it is necessary to keep track of the vertical variation in bed composition. In order to do this, the bed is divided into discrete layers. The top layer is the mixing or active layer and is the layer of sediment which is actively being exchanged with the bed and suspended loads. The temporal variation of the bed-material in the mixing and second layers is calculated as (Wu 2004) | |||
{{Equation| | |||
<math> | |||
\frac{\partial (\delta_m p_{bk}) }{\partial t} + \biggl( \frac{\partial \zeta}{\partial t} \biggr)_k = -\frac{\partial (\delta_m p_{bk}) }{\partial t} = p^*_{bk} \biggl(\frac{\partial \delta_m }{\partial t} + \frac{\partial \zeta }{\partial t} \biggr) | |||
</math>|11}} | |||
where <math> \delta_m </math> and <math> \delta_s </math> are the thicknesses of the mixing and second layers respectively. <math> p^*_{bk} = p_{bk} </math> for <math> \partial \zeta / \partial t + \partial \delta_m / \partial t \le 0 </math> or <math> p^*_{bk} = p_{sk} </math> otherwise. Figure 3 shows an example of the bed layer evolution over time for varying bed deposition and erosion. | |||
[[File:Bed_layering_V2.jpg|thumb|left|500px|Figure 3. Example of bed layer variation for varying deposition and erosion.]] | |||
<br style="clear:both" /> | |||
= Boundary Conditions = | |||
There are three types of boundary conditions in the sediment transport: Wet-dry, Outflow and Inflow. | |||
1. Wet-dry interface. | |||
:The interface between wet and dry cells has a zero-flux boundary condition. Both the advective and diffusive fluxes are set to zero at the wet-dry interfaces. Note that avalanching may still occur between wet-dry cells. | |||
2. Outflow Boundary Condition | |||
:Outflow boundaries are assigned a zero-gradient boundary condition and sediments are allowed to be transported freely out of the domain. | |||
3. Inflow Boundary Condition | |||
:When flow is entering the domain, it is necessary to specify the sediment concentration. In CMS-Flow, the inflow sediment concentration is set to the equilibrium sediment concentation. For some cases, it is desired to reduce the amount of sediment entering from the boundary such as in locations where the sediment source is limited (i.e. coral reefs). The inflow equilibrium sediment concentration may be adjusted by multiplying by a loading scaling factor and is specified by the Advanced Card NET_LOADING_FACTOR or SEDIMENT_INFLOW_LOADING_FACTOR. | |||
= Numerical Methods = | |||
The governing equations are discretized using the Finite Volume Method on a staggered, non-uniform Cartesian grid. Time integration is calculated with a simple explicit forward Euler scheme. Diffusion terms are discretized with the standard central difference scheme. Advection terms are discretized with either the first order upwind scheme or the second order Hybrid Linear/Parabolic Approximation (HLPA) scheme of Zhu (1991). The default advection scheme is HLPA but may be changed with the Advanced Card ADVECTION_SCHEME. | |||
= References = | |||
* Buttolph, A. M., C. W. Reed, N. C. Kraus, N. Ono, M. Larson, B. Camenen, H. Hanson, T. Wamsley, and A. K. Zundel. (2006). “Two-dimensional depth-averaged circulation model CMS-M2D: Version 3.0, Report 2: Sediment transport and morphology change.” Coastal and Hydraulics Laboratory Technical Report ERDC/CHL TR-06-9. Vicksburg, MS: U.S. Army Engineer Research and Development Center, U.S.A. | |||
* Camenen, B., and Larson, M. (2007). “A unified sediment transport formulation for coastal inlet application”. Technical Report ERDC-CHL CR-07-01. Vicksburg, MS: U.S. Army Engineer Research and Development Center, U.S.A | |||
* Parker, G., Kilingeman, P. C., and McLean, D. G. (1982). “Bed load and size distribution in paved gravel-bed streams.” J. Hydr. Div., ASCE, 108(4), 544-571. | |||
* Soulsby, R. L. (1997). Dynamics of marine sands, a manual for practical applications. H. R. Wallingford, UK: Thomas Telford. | |||
* Watanabe, A. (1987). “3-dimensional numerical model of beach evolution”. Proc. Coastal Sediments ’87, ASCE, 802-817. | |||
* Wu, W. (2004).“Depth-averaged 2-D numerical modeling of unsteady flow and nonuniform sediment transport in open channels”. J. Hydraulic Eng., ASCE, 135(10), 1013–1024. | |||
* van Rijn, L. C. (1985). “Flume experiments of sedimentation in channels by currents and waves.” Report S 347-II, Delft Hydraulics laboratory, Deflt, Netherlands. | |||
* Zhu, J. (1991). “A low diffusive and oscillation-free convection scheme”. Com. App. Num. Meth., 7, 225-232. | |||
* Zundel, A. K. (2000). “Surface-water modeling system reference manual”. Brigham Young University, Environmental Modeling Research Laboratory, Provo, UT. | |||
= External Links = | |||
* Aug 2006 Two-Dimensional Depth-Averaged Circulation Model CMS-M2D: Version 3.0, Report 2, Sediment Transport and Morphology Change [http://libweb.erdc.usace.army.mil/Archimages/705.PDF] | * Aug 2006 Two-Dimensional Depth-Averaged Circulation Model CMS-M2D: Version 3.0, Report 2, Sediment Transport and Morphology Change [http://libweb.erdc.usace.army.mil/Archimages/705.PDF] | ||
* Aug 2008 CMS-Wave: A Nearshore Spectral Wave Processes Model for Coastal Inlets and Navigation Projects [http://libweb.wes.army.mil/uhtbin/hyperion/CHL-TR-08-13.pdf] | * Aug 2008 CMS-Wave: A Nearshore Spectral Wave Processes Model for Coastal Inlets and Navigation Projects [http://libweb.wes.army.mil/uhtbin/hyperion/CHL-TR-08-13.pdf] | ||
[[Media:Presentation.pdf | Powerpoint presentation on NET]] | |||
---- | |||
[[CMS#Documentation_Portal | Documentation Portal]] | |||
[[category:CMS-Flow]] | |||
Latest revision as of 16:33, 6 November 2014
UNDER CONSTRUCTION
written by Alejandro Sanchez Last date modified: December 8, 2010
Total-load Transport Equation
The single-sized sediment transport model described in Sánchez and Wu (2011a) was extended to multiple-sized sediments within CMS by Sánchez and Wu (2011b). In this model, the sediment transport is separated into current- and wave-related transports. The transport due to currents includes the stirring effect of waves, and the wave-related transport includes the transport due to asymmetric oscillatory wave motion as well as steady contributions by Stokes drift, surface roller, and undertow. The current-related bed and suspended transports are combined into a single total-load transport equation, thus reducing the computational costs and simplifying the bed change computation. The 2DH transport equation for the current-related total load is
|
|
(1) |
for j= 1,2; k=1,2...,N, where N is the number of sediment size classes and
- = actual depth-averaged total-load sediment concentration [kg/m3] for size class k defined as in which is the total-load mass transport
- = equilibrium depth-averaged total-load sediment concentration [kg/m3] for size class k and described in the equilibrium concentration and transport rates section
- = total-load correction factor described in the Total-Load Correction Factor section [-]
- = fraction of suspended load in total load for size class k described in fraction of suspended sediments section [-]
- = horizontal sediment mixing coefficient described in the horizontal sediment mixing coefficient section [m2/s]
- = total-load adaptation coefficient described in the adaptation coefficient section [-]
- = sediment fall velocity [m/s].
In the above equation, the first term represents the temporal variation of ; the second term represents the horizontal advection; the third term represents the horizontal diffusion and dispersion of suspended sediments; and the last term represents the erosion and deposition. The equation may be applied to single-sized sediment transport by using a single sediment size class (i.e., N = 1). The bed composition, however, does not vary when using a single sediment size class. The units of sediment concentration used here are kg/m3 rather than dimensionless volume concentrations in order to avoid numerical precision errors at low concentrations.
In the above equations, it is assumed that the wave flux velocity is not included in the momentum equations. If the wave flux velocity is included, then the total flux velocity (V) should be used instead of the depth-averaged current velocity (U). The reason for this is because without a wave-induced sediment transport to counter the offshore directed transport due to the undertow, the model would predict excessive movement of sediment offshore.
Fraction of Suspended Sediment
In order to solve the system of equations for sediment transport implicitly, the fraction of suspended sediment must be determined explicitly. This is done by assuming
|
|
(2) |
where are the actual suspended- and total-load transport rates and are the equilibrium suspended- and total-load transport rates.
Adaptation Coefficient
The total-load adaptation coefficient is an important parameter in the sediment transport model. There are many variations of this parameter in literature (Lin 1984; Gallappatti and Vreugdenhil 1985; and Armanini and di Silvio 1986). CMS uses a total-load adaptation coefficient that is related to the total-load adaptation length (Lt ) and time (Tt) by
|
|
(3) |
where:
- = sediment fall velocity corresponding to the transport grain size for single-sized sediment transport or the median grain size for multiple-sized sediment transport [m/s]
- U = depth-averaged current velocity [m/s]
- h = water depth [m].
The adaptation length or time is a characteristic distance or time for sediment to adjust from non-equilibrium to equilibrium transport. Because the total load is a combination of the bed and suspended loads, the associated adaptation length may be calculated as are the suspended- and bed-load adaptation lengths. The symbol is defined as
|
|
(4) |
in which are the adaptation coefficient lengths for suspended load. The adaptation coefficient can be calculated either empirically or based on analytical solutions to the pure vertical convection-diffusion equation of suspended sediment. One example of an empirical formula is that proposed by Lin (1984):
|
|
(5) |
where u* is the bed shear stress, and is the von Karman constant. Armanini and di Silvio (1986) proposed an analytical equation:
| (6) |
where is the thickness of the bottom layer defined by is the zero-velocity distance from the bed. Gallappatti (1983) proposed the following equation to determine the suspended-load adaptation time:
| (7) |
where u* is the current related bottom shear velocity, .
The bed-load adaptation length (Lb) is generally related to the dimension of bed forms such as sand dunes. Large bed forms are generally proportional to the water depth, and, therefore, the bed-load adaptation length can be estimated as Lb = abh in which ab is an empirical coefficient on the order of 5-10. Although limited guidance exists on methods to estimate Lb, the determination of Lb is still empirical and in the developmental stage. For a detailed discussion of the adaptation length, the reader is referred to Wu (2007). In general, it is recommended that the adaptation length be calibrated with field data in order to achieve the best and most reliable results.
Total-load correction factor
The total-load correction factor (βtk) accounts for the vertical distribution of the suspended sediment concentration and velocity profiles as well as the fact that bed load travels at a slower velocity than the depth-averaged current velocity (Figure 1) (Wu 2007). By definition, βtk is the ratio of the depth-averaged total-load and flow velocities.
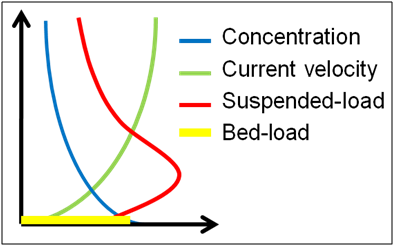
Figure 1. Schematic of sediment and current vertical profiles.
In a combined bed-load and suspended-load model, the correction factor is given by
| (8) |
where ubk is the bed-load velocity, and βsk is the suspended-load correction factor and is defined as the ratio of the depth-averaged suspended sediment and flow velocities. Since most sediment is transported near the bed, both the total- and suspended-load correction factors (βtk and βsk) are usually less than 1 and typically in the range of 0.3 and 0.7, respectively. By assuming logarithmic current velocity and exponential suspended sediment concentration profiles, an explicit expression for the suspended-load correction factor (βsk) may be obtained as (Sánchez and Wu 2011b)
| (9) |
where:
A = a/h [-]
Z = za/h [-]
= vertical mixing coefficient [m2/s]
a = reference height near the bed for the suspended load [m]
za = apparent roughness length [m]
(exponential integral).
The equation can be further simplified by assuming that the reference height is proportional to the apparent roughness length (e.g., a = 30zz) so that . Figure 2 shows a comparison of the suspended-load correction factor based on the logarithmic velocity with exponential and Rouse suspended sediment concentration profiles. Both cases show similar behavior for the suspended-load correction factor (). For fine sediments (small fall velocity), is close to 1.0 and experiences smaller influences by the bottom roughness, while for course sediments, can be as low as 0.5 and is largely influenced by the bottom roughness. This is to be expected since course sediments are transported more closely to the bottom, compared to fine sediments.
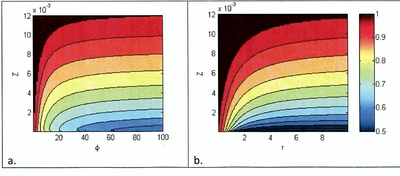
Figure 2. Suspended load correction factors based on the logarithmic velocity profile and (a) exponential and (b) Rouse suspended sediment profile. The Rouse number is
The bed-load velocity (ubk) in Equation 8 is calculated using the van Rijn (1984a) formula with re-calibrated coefficients from Wu et al. (2006):
| (10) |
where:
s = specific gravity [-]
g = gravitational constant (~9.81 m/s2)
dk = characteristic grain diameter for the kth size class [m]
= grain-related bed shear stress [Pa]
= grain-related Manning’s roughness coefficient [s/m1/3]
= critical bed shear stress for the kth size class [Pa].
Bed Change Equation
The change in the water depth is calculated by
| (11) |
where:
zb = bed elevation with respect to the vertical datum [m]
pm' = bed porosity [-]
= sediment (material) density (~2650 kg/m3 for quartz sediment)
Ds = empirical bed-slope coefficient (constant) [-]
is the bed-load mass transport rate magnitude [kg/m/s].
The first term on the right-hand side of the above equation represents the bed change due to sediment exchange near the bed. The last term accounts for the effect of the bed slope on bed-load transport. The bed-slope coefficient (Ds) is usually about 0.1 to 3.0. For a detailed derivation of the above equation, the reader is referred to Sanchez and Wu (2011a). The total bed change is calculated as the sum of the bed changes for all size classes:
| (12) |
Bed Sorting and Gradation (nonuniform sediments)
When simulating nonuniform sediments it is necessary to keep track of the vertical variation in bed composition. In order to do this, the bed is divided into discrete layers. The top layer is the mixing or active layer and is the layer of sediment which is actively being exchanged with the bed and suspended loads. The temporal variation of the bed-material in the mixing and second layers is calculated as (Wu 2004)
|
|
(11) |
where and are the thicknesses of the mixing and second layers respectively. for or otherwise. Figure 3 shows an example of the bed layer evolution over time for varying bed deposition and erosion.
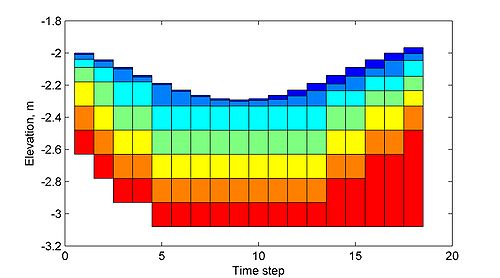
Boundary Conditions
There are three types of boundary conditions in the sediment transport: Wet-dry, Outflow and Inflow.
1. Wet-dry interface.
- The interface between wet and dry cells has a zero-flux boundary condition. Both the advective and diffusive fluxes are set to zero at the wet-dry interfaces. Note that avalanching may still occur between wet-dry cells.
2. Outflow Boundary Condition
- Outflow boundaries are assigned a zero-gradient boundary condition and sediments are allowed to be transported freely out of the domain.
3. Inflow Boundary Condition
- When flow is entering the domain, it is necessary to specify the sediment concentration. In CMS-Flow, the inflow sediment concentration is set to the equilibrium sediment concentation. For some cases, it is desired to reduce the amount of sediment entering from the boundary such as in locations where the sediment source is limited (i.e. coral reefs). The inflow equilibrium sediment concentration may be adjusted by multiplying by a loading scaling factor and is specified by the Advanced Card NET_LOADING_FACTOR or SEDIMENT_INFLOW_LOADING_FACTOR.
Numerical Methods
The governing equations are discretized using the Finite Volume Method on a staggered, non-uniform Cartesian grid. Time integration is calculated with a simple explicit forward Euler scheme. Diffusion terms are discretized with the standard central difference scheme. Advection terms are discretized with either the first order upwind scheme or the second order Hybrid Linear/Parabolic Approximation (HLPA) scheme of Zhu (1991). The default advection scheme is HLPA but may be changed with the Advanced Card ADVECTION_SCHEME.
References
- Buttolph, A. M., C. W. Reed, N. C. Kraus, N. Ono, M. Larson, B. Camenen, H. Hanson, T. Wamsley, and A. K. Zundel. (2006). “Two-dimensional depth-averaged circulation model CMS-M2D: Version 3.0, Report 2: Sediment transport and morphology change.” Coastal and Hydraulics Laboratory Technical Report ERDC/CHL TR-06-9. Vicksburg, MS: U.S. Army Engineer Research and Development Center, U.S.A.
- Camenen, B., and Larson, M. (2007). “A unified sediment transport formulation for coastal inlet application”. Technical Report ERDC-CHL CR-07-01. Vicksburg, MS: U.S. Army Engineer Research and Development Center, U.S.A
- Parker, G., Kilingeman, P. C., and McLean, D. G. (1982). “Bed load and size distribution in paved gravel-bed streams.” J. Hydr. Div., ASCE, 108(4), 544-571.
- Soulsby, R. L. (1997). Dynamics of marine sands, a manual for practical applications. H. R. Wallingford, UK: Thomas Telford.
- Watanabe, A. (1987). “3-dimensional numerical model of beach evolution”. Proc. Coastal Sediments ’87, ASCE, 802-817.
- Wu, W. (2004).“Depth-averaged 2-D numerical modeling of unsteady flow and nonuniform sediment transport in open channels”. J. Hydraulic Eng., ASCE, 135(10), 1013–1024.
- van Rijn, L. C. (1985). “Flume experiments of sedimentation in channels by currents and waves.” Report S 347-II, Delft Hydraulics laboratory, Deflt, Netherlands.
- Zhu, J. (1991). “A low diffusive and oscillation-free convection scheme”. Com. App. Num. Meth., 7, 225-232.
- Zundel, A. K. (2000). “Surface-water modeling system reference manual”. Brigham Young University, Environmental Modeling Research Laboratory, Provo, UT.
External Links
- Aug 2006 Two-Dimensional Depth-Averaged Circulation Model CMS-M2D: Version 3.0, Report 2, Sediment Transport and Morphology Change [1]
- Aug 2008 CMS-Wave: A Nearshore Spectral Wave Processes Model for Coastal Inlets and Navigation Projects [2]
Powerpoint presentation on NET