Wind Setup: Difference between revisions
Jump to navigation
Jump to search
| Line 4: | Line 4: | ||
== Analytical Solution == | == Analytical Solution == | ||
The analytical solution for wind setup over a constant depth is given by | The analytical solution for wind setup over a constant depth is given by | ||
\begin{equation} \tag{1} | |||
\eta = \sqrt{2 \frac{\rho_a C_d W^2}{\rho g} (x + C ) + h^2} - h | |||
\end{equation} | |||
where <math>\eta</math> is the water surface elevation, <math>\rho</math> is the water density, <math>\rho_a</math> is the air density, <math>g</math> is the gravitational acceleration, <math>W</math> is the wind speed, <math>h</math> is the water depth, and <math>C</math> is a constant of integration. | where <math>\eta</math> is the water surface elevation, <math>\rho</math> is the water density, <math>\rho_a</math> is the air density, <math>g</math> is the gravitational acceleration, <math>W</math> is the wind speed, <math>h</math> is the water depth, and <math>C</math> is a constant of integration. | ||
== Model Setup == | == Model Setup == | ||
Revision as of 14:35, 16 July 2012
UNDER CONSTRUCTION
Analytical Solution
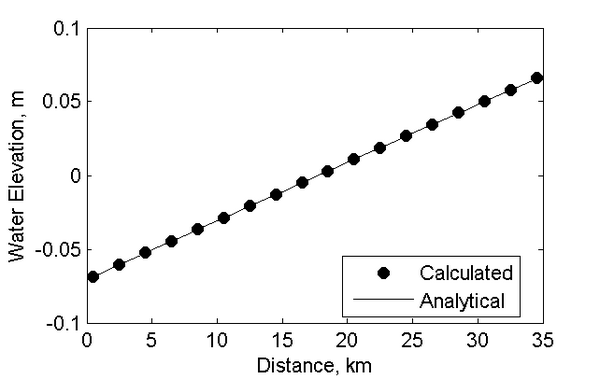
The analytical solution for wind setup over a constant depth is given by \begin{equation} \tag{1}
\eta = \sqrt{2 \frac{\rho_a C_d W^2}{\rho g} (x + C ) + h^2} - h
\end{equation}
where is the water surface elevation, is the water density, is the air density, is the gravitational acceleration, is the wind speed, is the water depth, and is a constant of integration.
Model Setup
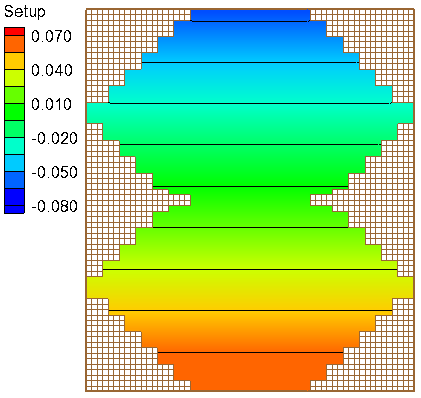
A computational grid with constant water depth of 5 m and irregular boundaries is used in order to test the model performance. The computational grid has 60 columns and 70 rows and a constant resolution of 500 m.
Results