CR-07-1:Chapter4

Suspended load

Introduction

The earliest transport rate formulas are mainly based on the concept that the sediment transport rate for steady uniform flow can be related to the bottom shear stress (Meyer-Peter and Müller 1948; Einstein 1950; Engelund and Hansen 1972) assuming that bed-load transport prevails. However, if the shear stress is sufficiently large, the particles can be lifted, put in suspension, and transported in large quantities by the current. Thus, suspended load often prevails for fine sediments (d₅₀ < 0.5 mm). The traditional approach for calculating the unsteady depth-averaged volumetric suspended load transport q_ss is to determine the vertical distribution of suspended sediment concentration (c) and velocity (u), after which the product between these two quantities is integrated through the vertical from the edge of the bed-load layer (z = z_a) to the water surface (z = h) (Van Rijn 1993), yielding:

\begin{equation} \tag{111}

 {{q}_{ss}}\left( t \right)=\int_{{{z}_{a}}}^{h}{u\left( z,t \right)c\left( z,t \right)dz}

\end{equation}

where q_ss(t) is the depth-averaged instantaneous suspended load per unit width, u(z,t) and c(z,t) are, respectively, the horizontal velocity and the volume sediment concentration at the height z, z_a is the level at the top of the bed-load layer, and h(t) is the instantaneous water depth. A steady situation is typically assumed to simplify the problem, so time-averaged values $u\left(z\right)={\overline {u\left(z,t\right)}}$ and $c\left(z\right)={\overline {c\left(z,t\right)}}$

are substituted (Figure 39):

\begin{equation} \tag{112} {{q}_{ss}}=\int_{{{z}_{a}}}^{h}{c\left( z \right)u\left( z \right)dz} \end{equation}

Therefore, an accurate estimation of the total suspended load requires accurate prediction of the mean current velocity and concentration profiles.

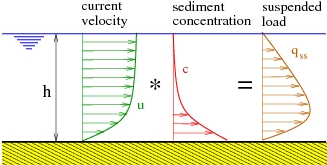
Figure 39. Computation of suspended load over depth.

In the marine coastal environment, the process of sediment transport becomes complex because of the presence of oscillatory flows and the interaction between steady and oscillatory flows. For longshore sediment transport, the effect of the short waves is typically modeled as an additional sediment stirring that increases the bed shear stress and the vertical mixing coefficient for the sediment in suspension (Bijker 1967; Watanabe 1982; Van Rijn 1993).

To describe suspended load above the wave boundary layer, some refined mathematical approaches were proposed during the last decades with sophisticated turbulence closure models (Fredsøe et al. 1985; Davies 1990; Davies et al. 1997). However, the development of practical sediment transport models still has a strong empirical character and relies heavily on physical insight combined with quantitative data obtained through laboratory and field experiments.

An essential part of morphodynamic computations for flow conditions involving suspended sediment transport is the use of a reference concentration as a bed boundary condition. Van Rijn (1984b) proposed that the reference concentration should be a function of the bed-load transport. Furthermore, the main controlling parameters for the suspended load are the settling velocity of the sediment W_s, and more specifically, the vertical sediment diffusion coefficient $\varphi _{v}$. The latter is examined here and compared to the Van Rijn (1984b) results.

In the nearshore, for mild wave conditions, the bed is covered by ripples. These bed forms strongly affect the sediment transport by enhancing the suspended load, but also by modifying the direction of the sediment transport. Assuming $u\left(z,t\right)={\overline {u\left(z,t\right)}}+{\tilde {u}}\left(z,t\right)=u\left(z\right)+{\tilde {u}}\left(z,t\right)$ and $c\left(z,t\right)={\overline {c\left(z,t\right)}}+{\tilde {c}}\left(z,t\right)=c\left(z\right)+{\tilde {c}}\left(z,t\right)$, where ${\tilde {u}}\left(z,t\right)$ and ${\tilde {c}}\left(z,t\right)$ are the oscillatory components, the net suspended sediment transport is obtained by averaging Equation 111:

\begin{equation} \tag{113}

 {{q}_{ss}}=<\int_{{{z}_{a}}}^{h\left( t \right)}{\left[ u\left( z \right)c\left( z \right)+\tilde{u}\left( z,t \right)\tilde{c}\left( z,t \right) \right]}dz>

\end{equation}

\begin{equation} \tag{114} ={{q}_{ss,c}}+{{q}_{ss,w}} \end{equation}

The first term on the right side (Equation 114) corresponds to the current-related suspended load, and the second term corresponds to the wave-related suspended load. The wave-related suspended load includes the quasi-steady suspended load due to asymmetric waves (assuming no phase lag exist between the wave velocity and the sediment concentration) and the unsteady effects due to a possible phase lag between the instantaneous velocity and concentration. Many experimental studies and most predictive models do not take into account the wave-related suspended load, although it appears to be significant for cross-shore sediment transport.

The objective of this study was to develop a reliable and general formulation for the prediction of suspended load transport valid under a wide range of fluvial and coastal conditions. For this purpose, various data sets were used for the model development including steady and oscillatory flows. The study focused on the prediction of the sediment concentration through the water column, establishing relationships for the vertical sediment diffusivity and the reference concentration. Assuming a typical velocity profile, the current-related suspended load can easily be calculated. The second part of this study focused on the possible phase lag affecting the suspended load in the wave direction due to the presence of ripples.

Equilibrium profile for suspended sediment

Mass conservation equation An equilibrium can exist between the settling velocity and the hydrodynamic forcing (Figure 40). The equation for the sediment concentration is derived from the mass conservation equation employed to compute changes in bottom topography:

\begin{equation} \tag{115} \frac{\partial c}{\partial t}+\text{div}\vec{F}=0 \end{equation}

with

\begin{equation} \tag{116} \vec{F}={{\vec{F}}_{a}}+{{\vec{F}}_{s}}+{{\vec{F}}_{d}} \end{equation}

where c is the sediment volume concentration (dimensionless), and F is the total sediment flux (consisting of contributions from advection, settling, and diffusion):

\begin{equation} \tag{117}

 \begin{align}
 & {{{\vec{F}}}_{a}}=c\ \vec{u}+c\ w\ {{{\vec{e}}}_{z}} \\
 & {{{\vec{F}}}_{s}}=-c\ {{W}_{s}}\ {{{\vec{e}}}_{z}} \\
 & {{{\vec{F}}}_{d}}=-{{\varepsilon }_{h}}\ \overrightarrow{\text{gra}{{\text{d}}_{\text{h}}}}\left( c \right)-{{\varepsilon }_{\nu }}\frac{\partial c}{\partial z}{{{\vec{e}}}_{z}} \\
 \end{align}

\end{equation}

with ${\vec {u}}$  the horizontal velocity vector, w the vertical velocity, ${{\vec {e}}_{z}}$  the unit vector in the vertical, ${\overrightarrow {{\text{gra}}{{\text{d}}_{\text{h}}}}}=\partial /\partial x+\partial /\partial y$ the horizontal gradient, and $\varepsilon _{v}$ and $\varepsilon _{h}$ the vertical and horizontal eddy diffusivity, respectively.

The bottom boundary condition yields the following relationship:

\begin{equation} \tag{118}

 -\left( {{{\vec{F}}}_{s}}+{{{\vec{F}}}_{d}} \right)\ \vec{n}=S

\end{equation}

where ${\vec {n}}$  is the unit vector perpendicular to the bottom, and S the erosion-deposition flux due to suspended load.

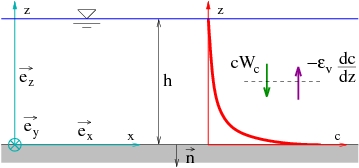
Figure 40. Concentration profile for steady conditions.

Several different expressions have been derived for the concentration profile, but most of them rely on the steady-state vertical diffusion equation (Figure 40). Under steady conditions ($\partial c/\partial t=0$, ${\text{div}}{{\vec {F}}_{a}}=0$,  ${\overrightarrow {{\text{gra}}{{\text{d}}_{\text{h}}}}}\left(c\right)=0\ {\text{and}}\ S=0$), Equation 115 may be simplified to:

\begin{equation} \tag{119}

 \frac{\partial c\left( z \right)}{\partial z}+\frac{{{W}_{s}}}{{{\varepsilon }_{v}}}c\left( z \right)=0

\end{equation}

Depending on the expression selected for $\varepsilon _{v}$ analytical solutions to Equation 119 of different type may be found. Thus, if $c\left(z={{z}_{a}}\right)={{c}_{a}}$, where z_a is the reference level (the maximum value of the computed roughness is often used):

\begin{equation} \tag{120}

 c\left( z \right)={{c}_{a}}\exp \left( -\int_{{{z}_{a}}}^{z}{\frac{Ws}{{{\varepsilon }_{v}}}dz} \right)

\end{equation}

Schmidt number An eddy viscosity coefficient is employed for determining the mixing, or diffusion coefficient. However, the mixing of sediment is not completely analogous to the mixing of water. The vertical eddy diffusivity of particles $\varepsilon _{v}$ is then related to the vertical eddy viscosity V_v through the Schmidt number s:

\begin{equation} \tag{121} \sigma =\frac{{{\varepsilon }_{v}}}{{{\nu }_{v}}} \end{equation}

In principle, s should be a constant, and s = 1. Three different processes were listed by Rose and Thorne (2001) to explain a deviation from unity:

• The first process to explain a s-values different from unity was proposed by Sumer and Deigaard (1981) and Van Rijn (1984b). They hypothesized that the centrifugal force in a fluid eddy causes sediment grains to be thrown outside of the eddy, which increases s.
• Another reason presented by Fredsøe and Deigaard (1994, pp. 231-234) for s to deviate from unity might be sediment settling out of the surrounding water before the water loses its earlier composition by mixing. This effect is particularly significant for the high concentration of cohesive sediments. Lees (1981) showed that s displayed a decreasing trend with increasing suspended sediment concentration.
• Rose and Thorne (2001) added that the estimation of s may be affected by the settling velocity, which varies because of the presence of turbulence.

Based on measurements by Coleman (1981), Van Rijn (1984b) suggested the following expression for s, which was defined as the ratio between the maximum sediment diffusivity and the maximum fluid eddy viscosity ($\sigma ={{\varepsilon }_{v,\max }}/{{\nu }_{v,\max }}$ with ${{\nu }_{v,\max }}=0.25\ \kappa {{u}_{*}}h$ for a parabolic profile):

\begin{equation} \tag{122}

 \sigma =1+2 { {\left( \frac{W_s}{u_*} \right)}^2}\text{    with    }0.1<\frac{W_s}{u_*}<1

\end{equation}

Sediment diffusivity and concentration profiles The sediment diffusivity $\varepsilon _{v}$ is a fundamental parameter for the estimation of the concentration profile, and it is a function of bottom roughness and shear stress, agitation (mainly due to waves), and settling velocity. Various distributions of the sediment mixing can be found in the literature, which typically produce either an exponential or a power-law sediment concentration profile.

Exponential profile. If the sediment diffusivity $\varepsilon _{v}$ is constant ($\varepsilon _{v}\approx 10^{-}12m^{2}$), an exponential profile is obtained for the mean concentration:

\begin{equation} \tag{123}

 c\left( z \right)={{c}_{R}}\exp \left( -\frac{{{W}_{s}}}{{{\varepsilon }_{v}}}z \right)

\end{equation}

where c_R is the reference concentration. The ratio W_s/$\varepsilon _{v}$ determines suspension conditions:

if W_s/$\varepsilon _{v}$ > 4: weak suspension,

if W_s/$\varepsilon _{v}$ < 0.5: strong suspension.

The sediment diffusivity is often described as a function of the shear velocity and the water depth according to:

\begin{equation} \tag{124} {{\varepsilon }_{v,E}}={{\sigma }_{E}}\ \kappa \ {{u}_{*}}\ h \end{equation}

where $\kappa$ is Von Karman's constant ($\kappa$ = 0.41), and s_E a constant consistent with the Schmidt number s.

Power-law profile. In the coastal zone, $\varepsilon _{v}$ is typically not expected to be constant over the depth, but a function of the agitation (mainly due to waves), bottom roughness, and settling velocity. For suspended sediment in a steady current, Rouse (1938) proposed a linear equation for the sediment diffusivity:

\begin{equation} \tag{125}

 {{\varepsilon }_{v,P}}={{\sigma }_{P}}\ \kappa \ {{u}_{*}}\ z

\end{equation}

with s_P being a constant consistent with the Schmidt number s that Rouse assumed equal to 1. This expression, nowadays widely used, gives the following expression for the concentration profile over depth:

\begin{equation} \tag{126}

 c\left( z \right)={{c}_{a}}{ {\left( \frac{z}{{{z}_{a}}} \right)}^{-{{W}_{s}}/{{\sigma }_{p}}\kappa {{u}_{*}}}}

\end{equation}

The parameter $P_{R}=W_{s}/(\kappa {u}{*})$ is commonly referred to as the Rouse parameter. It determines the shape of the suspended sediment profile, whereas the reference concentration c_a determines the magnitude of sediment in suspension at the reference level a:

• P_R > 5: near-bed suspension (h/10).
• 5 > P_R > 2: suspension through bottom half of boundary layer.
• 2 > P_R >1: suspension throughout the boundary layer.
• 1 > P_R: uniform suspension throughout the boundary layer.

The Rouse expression may be extended to a parabolic equation for the sediment diffusivity:

\begin{equation} \tag{127}

 {{\varepsilon }_{v,B}}={{\sigma }_{B}}\ \kappa \ {{u}_{*}}\ z\left( 1-\frac{z}{h} \right)

\end{equation}

where s_B is a constant consistent with the Schmidt number s. This expression implies the following solution for concentration profile over the depth:

\begin{equation} \tag{128}

 c\left( z \right)={{c}_{a}}{ {\left( \frac{z}{h-z}\frac{h-{{z}_{a}}}{{{z}_{a}}} \right)}^{-{{W}_{s}}/{{\sigma }_{B}}\kappa {{u}_{*}}}}

\end{equation}

Because $\varepsilon _{v}$ varies over the depth, different values for s_E, s_P, and s_B are obtained depending on the chosen profile. Figure 41 plots the three different analytic profiles (Equations 124, 125, and 127) with s_E = 1/2s_P = 1/6s_B assuming that the constant value for the sediment diffusivity was obtained from an average over the depth for the linear profile and the parabolic profile.

Experimental estimation of sediment diffusivity profile. If reliable point-concentration measurements are available, $\varepsilon _{v}$ may be calculated from (Vanoni 1946):

\begin{equation} \tag{129} {{\varepsilon }_{v}}=\frac{-{{W}_{s}}c}{dc/dz} \end{equation}

However, experimental estimation of the sediment concentration often induces non-negligible errors because in most situations a maximum of 10-15 points is available over the depth, implying that the estimated slope of the resultant curve is subject to large discrepancies.

In the following, the subscript v to indicate a vertical diffusivity will be dropped to simplify the notation.

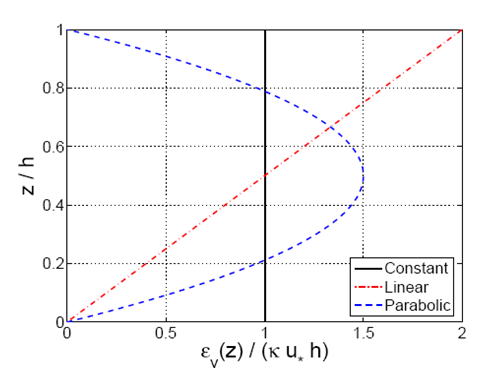
Figure 41. Three analytical relationships for vertical sediment diffusivity (Equations 124, 125, and 127) versus '''z'''/'''h 'with s = sE '= 1/2sP '= 1/6sB.

Sediment diffusivity due to steady current

Experimental data To investigate the sediment diffusivity profile in steady conditions, available data sets covering a wide range in conditions were compiled and analyzed. Table 15 summarizes these data sets, where the types of flow motion and sediment properties are listed. For all these experiments, sand with a relative density s = 2.65 was used. Most of these data sets were found in the SEDMOC (Van Rijn et al. 2001) data compilation.

Using the data sets summarized in Table 15, the shear velocity can be calculated from the measurements of the energy slope, but also directly from the measurements of the velocity profile. Figure 42 compares these two methods of computing the shear velocity. Even if a correlation is observed, a large scatter exists (see also Camenen et al. 2006). The energy slope method appears to be more consistent, because the calculation of the shear velocity from the velocity profile shows more scatter (the number of measurement points in the velocity profile is often limited, particularly close to the bottom).

Table 15. Data summary for suspended sediment experiments under steady currents.

Author(s)	Location	Flow Type	Number	d'50 '(mm)	b '(m)'	Fr '(-)'	U*c '(m/sec)'
Anderson (1942)	Enoree River, USA (1940-41)	River data	23	0.7	15	0.15-0.25	0.02-0.07
Barton & Lin (1955)	Fort-Collins, USA	Tilting flume	26	0.18	1.2	0.2-0.9	0.02-0,08
Laursen (1958)	Iowa, USA (1961-63)	Tilting flume	12	0.4, 1	0.9	0.25-0.60	0.02-0.09
Scott & Stephens (1966)	Mississippi River, USA (1961-63)	River	23	0.4	500	0.11-0.16	0.05-0.13
Culbertson et al. (1972)	Rio Grande River, USA (1965-66)	River	22	0.18-0.33	20	0.3-0.6	0.05-0.15
Voogt et al. (1991)	Krammer Beach, The Nederlands (April 1987)	Tidal channel	60	0.22-0.35	300	0.1-0.5	0.03-0.15
Damgaard et al. (2003)	Wallingford, Great Britain	Duct experiments	24	0.08-0.20	0.6	0.2-0.4	0.01-9.14

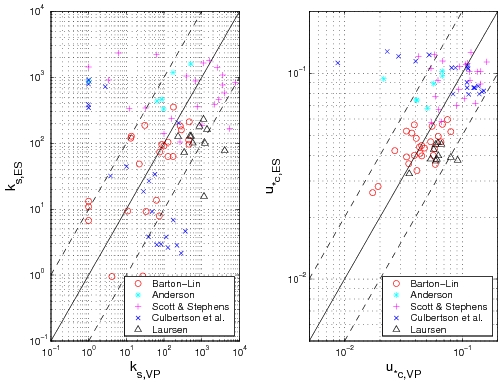
'Figure 42. Comparison between "energy slope" (ES) method and "velocity profile" method (VP) to estimate the Nikuradse roughness '''ks 'and shear velocity '''u_*c.

The experimental values obtained from each sediment concentration profile in the data sets are plotted (Figure 43) using Equation 129 and a point-by-point method yielding an estimate of the diffusivity according to:

\begin{equation} \tag{130}

 {{\varepsilon }_{c,i}}=\frac{-{{W}_{s}}c(i)}{\left\{ c\left( i+1 \right)-c\left( i-1 \right)/\left[ z\left( i+1 \right)-z\left( i-1 \right) \right] \right\}}

\end{equation}

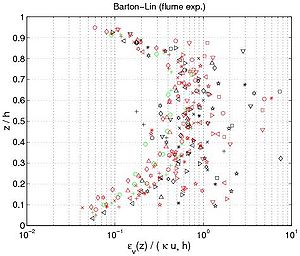
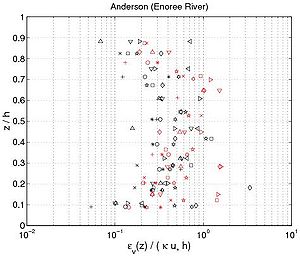
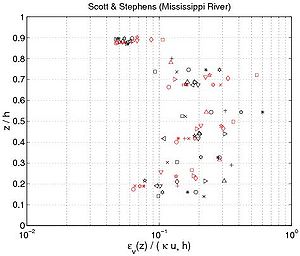
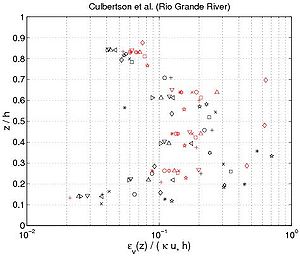
where i + 1 indicates consecutive experimental points along the z-axis for the concentration profile, and $\varepsilon$_c,i is the estimated sediment diffusivity at level z = z(i). Figure 43 confirms several results obtained previously. First, the sediment diffusivity is a linear function of the shear velocity u_*c and the water depth h. Nevertheless, it appears that the mean values obtained for z $\approx$ h/2 (where $\varepsilon _{c}$ is not function of z), depends on other parameters. Based on analysis of the different data set, the mean value varies from 710 ² m²/sec to 1 m²/sec. Moreover, $\varepsilon _{c}$ appears to be an increasing function of z if $z/h\leq 0.3$, a constant value for $0.3\leq z/h\leq 0.7$, and a decreasing function of z if $z/h\leq 0.7$. Thus, referring to these results and the curves obtained in Figure 41, the best of the three analytic profiles previously discussed is the parabolic profile (Equation 127). Van Rijn(1984b) also proposed the following equations to compute the current-related sediment diffusivity:

\begin{equation} \tag{131}

 \begin{align} {{\varepsilon }_{c}}
 &=\kappa \sigma {{u}_{*}}\ z(1-z/h)&\mbox{if {z}<0.5 h} \\
 &=0.25\kappa \sigma {{u}_{*}}\ h   &\mbox{if 0.5 h<z} 
 \end{align}

\end{equation}

Van Rijn (1984b) assumed that the sediment diffusivity is constant in the upper part of the water column. However, from the experimental results, a decrease is clearly observed if $z/h\leq 0.7$. Equation 131, which produces a complex equation for the concentration profile, does not appear to improve the results compared to the parabolic profile.

Finally, for the data sets from Voogt et al. (1991) and Damgaard et al. (2003), measurements of the energy slope were not made, and the calculation of the shear velocity from the velocity profile shows significant scatter. Therefore, results obtained for these two data sets are not presented in Figure 43.

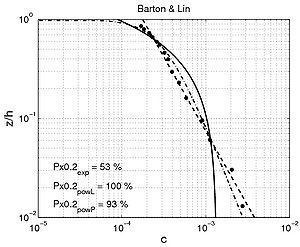
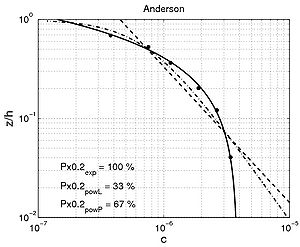
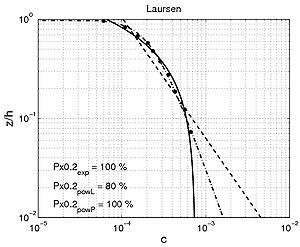
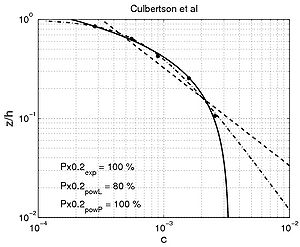
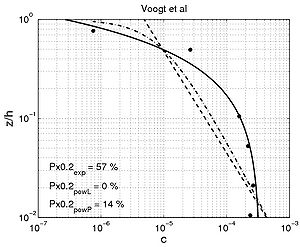
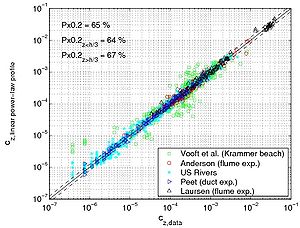
Shape of concentration profile Power-law and exponential concentration profiles were fitted to the measurements (Table 15). For a power-law profile, both linear and parabolic sediment diffusivity were examined. Some typical examples of the fit for these profiles are presented in Figure 44 for each of the data sets. Table 16 lists the percentage of sediment concentration values predicted within a range of 20 percent error of the measurements presented for the different data sets (symbolized by pred_20,meas, pred_20,powL, and pred_20,pow for the fit of the exponential-law and the "linear" and "parabolic" power-laws, respectively in Figure 45). These calculations were also performed for sediment concentration data closer to the bed (z < h/3) and in the upper layer (z > h/3), where the velocity is approximately constant.

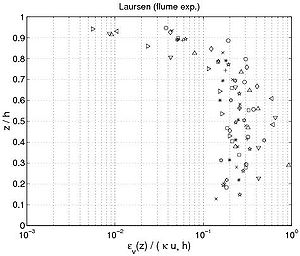Figure 43. Vertical profile of sediment diffusivity obtained from Equation 129 using measured concentration profiles (each symbol corresponds to a particular profile).

Table 16. Percentage of predictions of sediment concentration within +/- 20 percent of measured values obtained using an exponential law or power law
(linear and parabolic profile) for $\varepsilon _{c}$ in fitting against data.

Authors(s)	Exponential-Law Profile (%)							Power-Law Profile (linear) (%)	Power-Law Profile (parab.) (%)
	z	z '< '''h'''/3'	z '> '''h'''/3'	z	z '< '''h'''/3'	z '> '''h'''/3'	z	z '< '''h'''/3'	z '> '''h'''/3'
Barton & Lin	69.4	51.1	80.3	85.7	80.2	89.1	76.1	67.8	81.3
U.S. Rivers	66.4	60.3	72.5	62.1	64.8	59.5	71.4	71.4	71.5
Voogt et al.	46.6	38.4	62.2	36.5	37.6	34.5	48.9	44.6	57.1
Damgaard	82.5	82.5	-	90.0	90.0	-	90.8	90.8	-
Laursen	96.9	100	95.8	85.7	85.2	85.9	92.9	100	90.1
Total	65.6	57.0	75.8	65.4	63.5	67.4	69.9	66.4	74.1

---

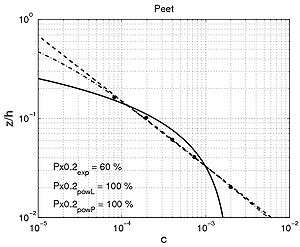Figure 44. Examples of comparisons between predicted concentration profiles, using fitted exponential (solid line) or power-law profiles (dashed line), and measured concentration.

---

---- (a)	(b)
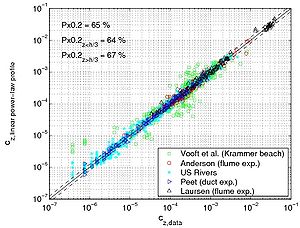(c)

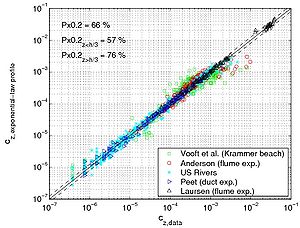Figure 45. Comparison between predicted concentration using fitted exponential profile (a), "linear" power-law profile (b), or "parabolic" power-law profile (c), and measured concentration using all data.

The main observation from this study is that there is no obvious law that fits all the measurements. However, the exponential law tends to yield better results for the upper part of the water column, whereas the linear power-law profile shows slightly better agreements closer to the bed. The parabolic power-law profile tends to produce better overall results as it presents nearly as good results as for the exponential profile in the upper part of the water column and even better results than the linear power-law profile in the lower part of the water column. This result confirms the idea of Van Rijn (1984b), who proposed an expression for the sediment diffusivity that linearly depends on the distance to the bed z close to the bed and is constant for z > h/2. However, large differences between the two laws are found depending on the data set. Thus, the data sets obtained from Barton and Lin (1955) and Damgaard et al. (2003) are better described by a power-law profile, whereas the data sets obtained from Voogt et al. (1991) and Laursen (1958) exhibit better agreement with an exponential profile. All the data points are plotted (Figure 45) comparing predicted and measured sediment concentrations. It can be seen that larger discrepancy appears in using the power-law profile for the three U.S. rivers data sets, whereas larger discrepancy appears using the exponential law profile with the Barton and Lin (1955) data set.

It should also be noted that the parabolic power-law profile produces a concentration equal to zero at the level z = h, although the two other laws allows a non-zero value. In breaking waves, the sediment diffusivity is clearly different from zero at z = h, which means that the parabolic power-law profile may not be used in the presence of breaking waves. For an expression that is applicable for both current and waves, the exponential law seems to be the most appropriate.

Estimation of Schmidt number Based on concentration profiles obtained from the compiled data set (Table 15), the fitted power-law and exponential profiles allow for an estimate of the Schmidt number. As discussed previously, the parabolic power-law profile for the sediment diffusivity ?_c produces the best qualitative agreement with the observed profiles. For that reason, a good correlation between s_B and s is expected, and s_B is calculated using Equation 128:

\begin{equation} \tag{132} {{\sigma }_{B}}=\frac{-{{W}_{s}}}{{{\alpha }_{B}}\kappa {{u}_{*c}}} \end{equation}

where a_B is the observed slope of the power-law relationship obtained by fitting to the data (the s_P-value is obtained in a similar manner).

Some additional data were compiled (Table 17) from the studies by Rose and Thorne (2001), who also estimated s_c assuming a Rouse concentration profile, and from Van Rijn (1984b), who used the Coleman (1970)data.

Combining data sets listed in Table 15 and the data listed in Table 17, a similar expression as the one Van Rijn (1984b) proposed was found (Figure 46):

\begin{equation} \tag{133}

 {{\sigma }_{c}}\approx {{\sigma }_{B}}=0.6+6{ {\left( \frac{{{W}_{s}}}{{{u}_{*c}}} \right)}^{2}}

\end{equation}

Table 17. Data summary for analysis on Schmidt number ('''d_''''s'_' 'corresponds to median grain size in suspension).

Author(s)	Location	Number	ds '(m)'	U*C '(m/sec)'	h '(m)'
Coleman (1970)	Flume experiments	16	1.49 - 2.10 10-4	0.02 - 0.06	0.4 - 0.8
Whitehouse (1995)	Thames estuary, UK	4	9 10-5	0.56 - 0.61	5 +/1 2
Green et al. (1999)	Tanukau Harbour, NZ	2	1.3 10-5	0.35, 0.45	12-15
Rose & Thorne (2001)	Taw estuary, UK	4	1.2 1.3 10-4	0.41 - 0.63	1.8 - 2.8

This equation produces a critical value for $W_s/u_{*c} \approx 0.25$, yielding $\sigma _c = 1$. Up to this critical value, the centrifugal forces in the fluid eddies produce an increasing $\sigma_c$. Equation 133 presents improved results compared to previous predictive formulas, as shown in Table 18 and Figure 46.

Table 18. Prediction of Schmidt number using parabolic profile
or an exponential profile for steady current.

Author(s)	$\sigma_c \approx \sigma_B$ (Equation 132)				$\sigma_c \approx 6 \sigma_E$ (Equation 135)
	Px1.5 %	Px2 %	Mean $(f(\sigma_c))$	Std $(f(\sigma_c))$	Px1.5 %	Px2 %	Mean $(f(\sigma_c))$	Std $(f(\sigma_c))$
Van Rijn (Equation 123)	53	78	-0.02	0.25	54	84	-0.08	0.22
Rose & Thorne	58	75	0.02	0.32	63	84	-0.04	0.27
Equation 133	52	78	0.03	0.27	68	90	-0.02	0.19
Equation 136	50	76	-0.04	0.26	68	88	-0.09	0.18

Using the exponential law to estimate the sediment diffusivity, for a steady current Equation 124 reduces to:

\begin{equation} \tag{134}

 \varepsilon_{c,E}=\sigma_E \kappa u_{*c} h \approx
 \frac{\sigma_c}{6} \kappa u_{*c} h

\end{equation}

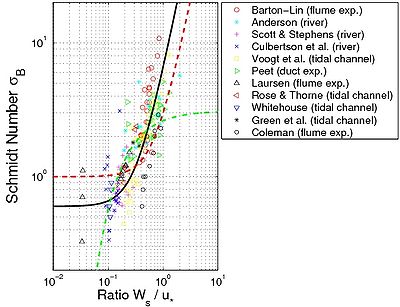
Figure 46. Estimation of Schmidt number (assumed equal to $\sigma_B$) as function of ratio $W_s/u_{*c}$ (solid line corresponds to Equation 133, dashed line to Equation 122, proposed by Van Rijn (1984b), and dashed-dotted line to Rose and Thorne (2001) formula).

It is also possible to calculate the coefficient s_E for the data:

\begin{equation} \tag{135}

 \sigma_E = \frac{-W_s}{\alpha_E \kappa u_{*c} h}

\end{equation}

where $a_E$ is the observed slope of the exponential-law relationship. Using the discussed data sets, an expression for $\sigma_E$ could be $\sigma_E = 1/6 \sigma_B$ following the results obtained for the parabolic profile where $\varepsilon_{c,E}=1/6\int_{0}^{h}{\varepsilon_{c,B} dz}$. It may be noted that $\sigma_E$ is roughly six times smaller than $\sigma_B$ (Figure 47), except for the data from Voogt et al. (1991) and from Damgaard et al. (2003), where $\sigma_E \approx 1/7$ and $1/15\sigma_B$, respectively. Similarly, $\sigma_E$ is roughly 2 to 3 times smaller than $\sigma_P$. The deviation from the theory may owe to the fact that the sediment concentration profiles were not measured through the entire water column.

Table 18 list the percentage of predicted values of the Schmidt number within a factor 0.5 and 2 (denoted Px1.5 and Px2, respectively) of the measurements presented together with the mean value and standard deviation of the function $f\left({{\sigma }_{c}}\right)=\log \left({{\sigma }_{c,pred}}/{{\sigma }_{c,meas}}\right)$. Equation 132 (from power law) and Equation 135 (from exponential law) were employed to estimate the Schmidt number. The spread in the results seems smaller if the Schmidt number is estimated from the exponential profile. Equation 133 yields similar results to the existing formulas if Equation 132 is employed, but improved results are obtained if Equation 135 is used (Table 18, Figure 48).

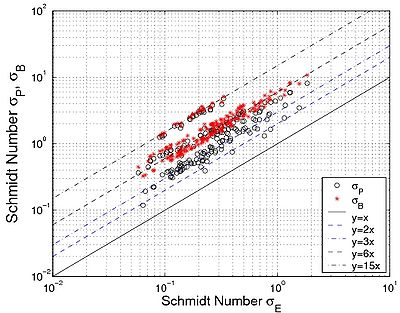
Figure 47. Estimated coefficient '''sE 'compared to coefficients sP 'and sB.

To put forward a relationship that gives physically meaningful results for all cases, it should be considered that the previous equations are correct only for W_s/u_*c < 1. For very small values of u_*c, the Schmidt number must be equal to 1, or s_E ? 1/6s_B. Thus, a new expression for s_E is proposed here (Figure 48):

\[{{\sigma }_{E}}=\left\{ \begin{align}

 & 0.7+3.6{{\sin }^{2}}\left( \frac{\pi }{2}\frac{{{W}_{s}}}{{{u}_{*c}}} \right)
   \text{if}\frac{{{W}_{s}}}{{{u}_{*c}}}\le 1 \\
 & 1.0+3.3{{\sin }^{2}}\left( \frac{\pi }{2}\frac{{{u}_{*c}}}{{{W}_{s}}} \right)
   \text{if}\frac{{{W}_{s}}}{{{u}_{*c}}}>1 \\

\end{align} \right.\qquad \qquad \qquad \text{(136)}\]

This equation presents slightly better results compared to Equation 133 (multiplied by 1/6, Table 18). Nevertheless, the data from the Damgaard et al. (2003) experiments are in general overestimated. This may be due to measurements only being carried out close to the bed (z < h/5).

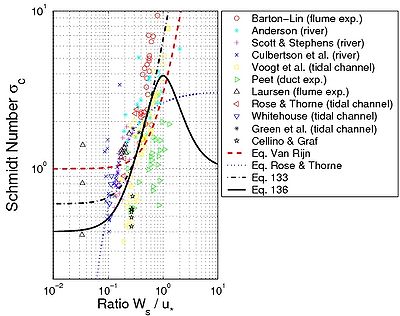
Figure 48. Estimated values of Schmidt number as function of ratio '''Ws/'''u_*c, together with predictive equations.

Sediment diffusivity in nonbreaking waves

The vertical distribution of suspended sediment outside the surf zone is mainly controlled by the downward settling of sediment particles, their resuspension, and the upward mixing of particles due to the generation of turbulence in boundary shear produced by friction at the seabed.

Theoretical profiles The eddy diffusivity for suspended sediment in nonbreaking waves may be defined as a constant, a linear, or a parabolic function of the vertical position relative to the water surface (or water depth):

\begin{equation} \tag{137}

\varepsilon_{w,E}=\sigma_E \kappa u_{*w} h

\end{equation}

\begin{equation} \tag{138}

\varepsilon_{w,P}=\sigma_P \kappa u_{*w} Z

\end{equation}

\begin{equation} \tag{139}

\varepsilon_{w,B}=\sigma_B \kappa u_{*w} Z \left(1-\frac{z}{h}\right)

\end{equation}

where $u_{*w}=\sqrt{\tau_w / \rho}$ is the shear velocity produced by the waves. Here, $\tau_w$ is the maximum shear stress due to the waves, and $\sigma_E$, $\sigma_P$, and $\sigma_B$ are the Schmidt numbers for an exponential, linear power-law, or parabolic power-law concentration profile, respectively.

Estimation of sediment diffusivity profiles for oscillatory flows To investigate the sediment diffusivity profile under oscillatory conditions, existing data sets covering a wide range of conditions were compiled and analyzed. Table 19 summarizes the data sets employed, where the flow-generation, sediment properties, and bed form characteristics are included. For all these experiments, sand with a relative density of s = 2.65 was used. Most of these data sets were compiled in the SEDMOC (Van Rijn et al. 2001) data set except those from Peters (2000), Gailani and Smith (2000), Bayram et al. (2001), and Wang et al. (2002).

For the extensive field data set from Gailani and Smith (2000), only two measurements of the concentration were provided over the depth. Also, for the data set from Peters (2000), only the parameters in the fitted exponential function (c_R and ?) were provided. Thus, these data sets were not consulted for a detailed study of the concentration profile. In the data set from Dohmen-Janssen (1999), the measurements were made close to the bed, within the sheet-flow layer. Thus, it will not be used for the estimation of the suspended load (as it corresponds to bed load), but only for investigating the behavior of the sediment diffusivity profile.

For each data set where the number of measurements of the concentration over the water column was sufficient (n > 5), the parameter values obtained from each sediment concentration profile were calculated over the water column using Equation 130.

Using the data sets presented in Table 19, the total shear velocity was estimated assuming that the shear velocities produced by the current or waves, respectively, can be linearly added. For most of the cases (wave flumes), the shear stress due to the current is much smaller than the shear stress due to the waves, and thus, may be neglected. The total Nikuradse roughness k_st was estimated using the method proposed by Soulsby (1997) by adding the grain-related, form-drag, and sediment transport roughness, k_s,g, k_s,r, and k_s,sf, respectively, assuming that the effects of waves prevail:

\begin{equation}\tag{140} k_{s,t}=k_{s,g}+k_{s,r}+k_{s,sf} \end{equation}

where $k_{s,sf}$ was obtained from the Wilson (1966, 1989a, b) formula and $k_{s,r}$ using the following formula:

\begin{equation} \tag{141} k_{s,r}=\alpha_r \frac{H_r^2}{L_r} \end{equation}

where $H_r$ and $L_r$ are the ripple height and length, and $\alpha_r$ is a constant ($\alpha_r = 0.25$). If the ripple characteristics were not measured, the Van Rijn (1989) formulas, proposed for irregular waves, were used (Equation 38).

The uncertainty involved in estimating the Nikuradse roughness and the ripple geometry explains the large scatter (Figures 49 and 50) as compared to the steady flow data previously discussed.

---

Table 19. Data summary for suspended sediment experiments under oscillatory flows.

Author(s)	Location	Flow Facility	Number	d'50 '(mm)	h '(m)'	Uc '''''''(m/sec)	Uw'1 '(m/sec)	Tw'1 '(sec)	Hr '(m)'	Lr '(m)'
Bosman (1982) and Steetzel (1985)	DHL, The Netherlalnds	Wave flume	70 (50)*	0.10	0.1 - 0.65	0.10 -0.32	0.13 - 0.30	1.4 - 2.0	0.01 - 0.03	0.08
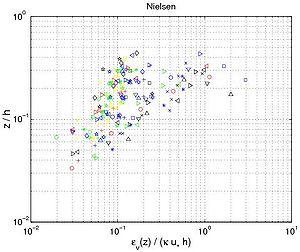
Nielsen (1984)	Australian beaches (1980-82), Australia	Field	65 (39)*	0.11 - 0.62	0.8 - 1.8	0 - 0.54	0.28 - 0.80	5.3 - 14.4	02 - 0.20	02 - 1.5
Steetzel (1984) and Van der Velden (1986)	DHL, The Netherlands	Small water tunnel	259 (259)*	0.10 - 0.36	0.4	0	0.07 - 0.65	1.0 - 7.0	0.005 - 0.1	0.011 - 0.55
Dette & Uliczka (1986)	Hannover, Germany	Large wave flume	11 (0)*	0.33	0.9 - 2.6	0	0.95 - 1.65	6.0	--3	--3
Kroon (1991)	Egmond beach (1989-90), The Netherlands	Field	31 (11)*	0.30 - 0.47	0.4 - 1.5	-0.55 - 0.97	0.20 - 0.91	3.1 - 12.6	0.005 - 0.05	0.15 - 0.75
Havinga (1992)	VinjeBasin, Delft, The Netherlands	Basin	28 (28)*	0.10	0.40 - 0.43	0.10 - 0.32	0 - 0.80	2.1 - 2.3	--3	--3
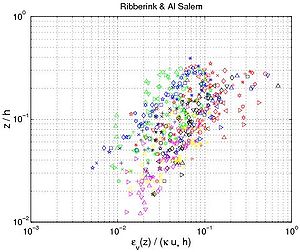
Ribberink & Al Salem (1994)	DHL, Delft, The Netherlands	Large water tunnel	71 (71)*	0.21	0.8	0	0.2 - 1.5	2.0 - 12.0	02 - 0.35	02 - 3.0
Dohmen-Janssen (1999)	DHL, Delft, The Netherlands	Large water tunnel	9	0.13 - 0.32	0.80	0.03 - 0.43	0.59 - 1.07	4.0 - 12.0	02	02
Chung et al. (2000)	Deltaflume, DHL, Delft, The Netherlands	Large wave flume	19 (19)*	0.16 - 0.33	3.5 - 4.5	-0.04 - -0.02	0.56 - 0.67	6.6 - 7.1	0.03 - 0.05	0.25 - 0.75
Peters (2000)	Großen Wellenkanal GWK, Hannover, Germany	Large wave flume	349 (0)*	0.12 - 0.33	0.4 - 2.4	-0.35 - 0.14	0.49 - 1.24	5.5
Gailani & Smith (2000)	Mouth Columbia River, Washington, USA	Field	818 (818)*	0.22	16.6 - 19.5	0 - 0.88	0.03 - 1.49	4.8 - 21.3	--3	--3
Voulgaris & Collins (2000)	Bournemouth beach, Caswell Bay, Rhossili Bay, UK	Field	12 (12)*	0.21, 0.26, 0.33	0.4 - 2.1	0.01 - 0.10	0.16 - 0.40	3.2 - 9.1	--3	--3
SEDMOC data set (Van Rijn et al. 2001) -Vessem-	Eastern Scheldt estuary (1983-84), The Netherlands	Field	70 (70)*	0.15	0.7 - 4.0	0.05 - 0.65	0.02 - 0.40	2.0 - 3.2	0.05	--3
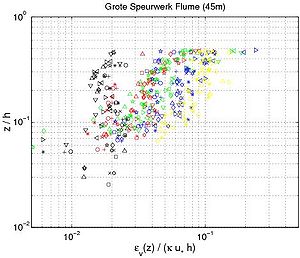
SEDMOC data set (Van Rijn et al. 2001)	Grote Speurwerk (35 m), DUT, Delft, The Netherlands	Wave flume	125 (81)*	0.10 - 0.22	0.29 - 0.60	0.07 - 0.45	0.17 - 0.55	1.2 - 2.7	0.002 - 0.029	0.006 - 0.20
SEDMOC data set (Van Rijn et al. 2001)	Grote Speurwerk (45 m), DUT, Delft, The Netherlands	Wave flume	62 (62)*	0.15 - 0.29	0.49 - 0.55	0.16 - 0.35	0.14 - 0.60	2.4 - 2.8	--3	--3
SEDMOC data set (Van Rijn et al. 2001)	Deltaflume, DHL, Delft, The Netherlands	Large wave flume	57 (30)*	0.19 - 0.24	0.7 - 3.4	-0.18 - 0	0.67 - 1.46	2.6 - 5.0	02 - 0.04	02 - 1.0
Bayram et al. (2001)	Sandy-Duck (1996-98), SC, USA	Field	66 (25)*	0.18 - 0.20	1.2 - 8.6	0.04 - 1.32	0.71 - 2.13	8.0 - 12.8	--3	--3
Wang et al. (2002)	LSTF, Vicksburg, MS, USA	Large basin	14 (0)*	0.22	0.10 - 0.40	0 - 0.18	0.27 - 0.45	1.5, 3.0	--3	--3
NOTE: Delft Hydraulics Laboratory (DHL), Delft University of Technology (DUT), Large-scale Sediment Transport Facility (LSTF). Number of nonbreaking cases. 1 Random waves, Us is computed from the root-mean-square wave height and Tw = Tp. 2 Flat bed. 3 Not available.

---

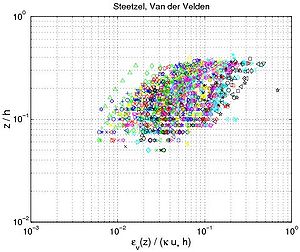
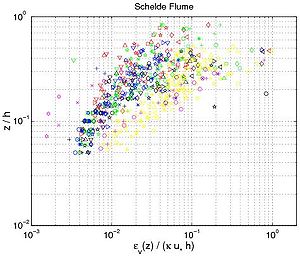
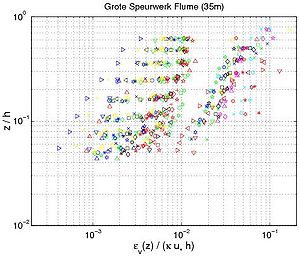
From Figures 49 and 50, three regions are observed regarding the sediment diffusivity profile under oscillatory flow. Close to the bottom, the sediment diffusivity reaches a minimum value and seems to be constant (the data sets from "Schelde Flume," Ribberink and Al Salem, Dohmen-Janssen). Above this region, the sediment diffusivity is a linear function of the elevation z/h until it reaches a maximum value (the data sets from "Grote Speurwerk Flume," Ribberink and Al Salem (1994), Dette and Ulickza (1986); and "Delta Flume"). Thus, as proposed by Van Rijn (1989), the sediment diffusivity for non-breaking waves may be described by the following equations:

\[\begin{align}

& z\le \delta_m \qquad\qquad \varepsilon_w = \varepsilon_{w,bed} \\
& z\ge z_w      \qquad\qquad \varepsilon_w = \varepsilon_{w,max} \\
& \delta_s <z < z_w \qquad  \varepsilon_w = \varepsilon_{w,bed}+\left( \varepsilon_{w,max} - \varepsilon_{w,bed} \right)\frac{z-\delta_m}{z_w-\delta_m} \\

\end{align}\qquad \qquad \text{(142)}\]

where d_m is the moving mixing layer (found to be equal to about three times the ripple height in the ripple regime, and three times the boundary layer thickness in the sheet-flow regime), and z_w is the elevation from where the sediment diffusivity appears to be approximately constant over the depth (VanRijn 1989 proposed z_w = 0.5h). Kosyan (1985) showed that the monotonic increase of the diffusion coefficient may be caused by to the orbital motion of the waves, whereas the constant value at the bottom may be caused by the friction between the moving fluid mass and the rough bottom.

From the data set of Dohmen-Janssen (1999), measurements were provided close to and inside the fixed bed. The calculation of the sediment diffusivity in this region is much more difficult because of the estimation of the hindered settling velocity (close to the bed, W_s decreases markedly with increasing sediment concentration). The Richardson and Zaki (1954) equation (Equation 10 with a = 4) limits the peak of the sediment diffusivity close to the bottom compared to a constant value for W_s. It appears that the sediment diffusivity increases strongly after entering the fixed bed. However, the advection-diffusion equation (Equation 115 to 117) is not valid anymore.

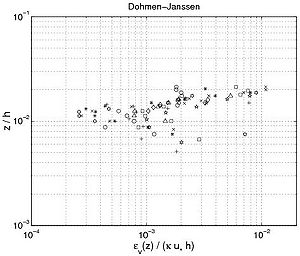Figure 49. Vertical profiles of eddy diffusivity obtained from Equation 130 using measured concentration profiles with interaction between nonbreaking waves and current (data from wave flumes and water tunnels; each symbol corresponds to particular profile).

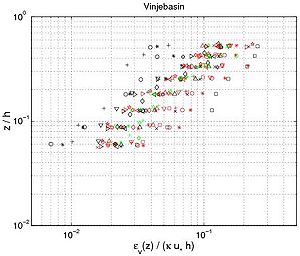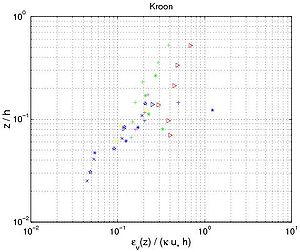
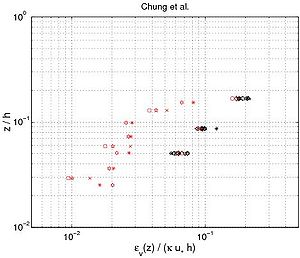
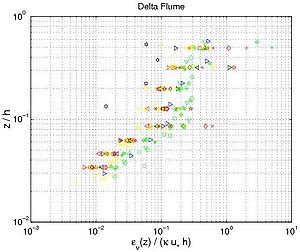
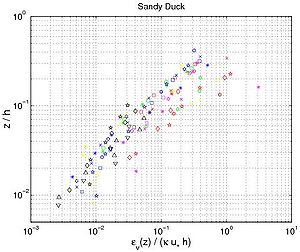
Figure 50. Vertical profile of eddy diffusivity obtained from Equation 130 using measured concentration profiles with interaction between nonbreaking waves and current (data from large-scale facilities and field measurements; each symbol corresponds to particular profile).

Starting point for suspended load A difficulty in estimating the suspended sediment load is to determine the elevation that separates suspended load and bed load. For the sheet-flow mode, this elevation should be at the top of the sheet-flow layer. Dohmen-Janssen (1999) defined the top of the sheet-flow layer as the maximum concentration where the interaction between the particles cannot be neglected, i.e., for a volume concentration of c ? 0.08. Figure 51 plots the concentration c versus the elevation z/h using the data from Dohmen-Janssen (1999). These data show some of the first measurements of large concentration close to the bottom in the sheet-flow regime (the sediment diffusivity profiles calculated from these sediment concentration profiles are shown in Figure 49). It appears that, in the sheet-flow layer, the concentration drops from c₀ ? 0.4-0.7 inside the fixed bed to c_b < 0.08 above the sheet flow. A two-phase model in which the granular interactions are described by application of the kinetic theory appeared to be the more accurate model to describe the sediment concentration profile inside the sheet-flow layer (Jenkins and Hanes 1998; Dohmen-Janssen and Hanes 2002).

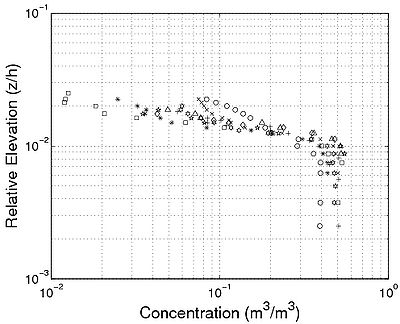
Figure 51. High sediment concentration close to bottom using data from Dohmen Janssen (1999) (elevation '''z 'was increased by 1 cm to allow for logarithmic representation).

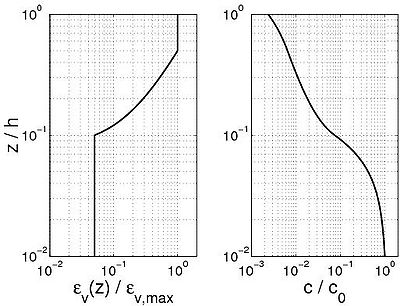
A simplified formula was developed to estimate a characteristic sediment concentration profile assuming a maximum value c = c₀ for the fixed bed and a distribution of the sediment diffusivity given by Equation 142 for the suspended sediment. The concentration profile is obtained by applying the advection-diffusion equation taking into account the hindered fall velocity (Equation 10). It can be observed (Figure 52(a)) that such a simple formula produces realistic sediment concentration profiles over the depth. For this calculation, ?_w,max = 5 10^-3 m²/sec, ?_w,bed = 1 10^-4 m²/sec, z_w = 0.5h, d_m = 0.1h (in Equation 142) and the coefficient n = 1 were chosen to allow for a correct decrease in concentration in the sheet-flow layer. The bed concentration c_b defined at the top of the moving mixing layer (d_m is here assumed to be equal to the sheet-flow layer d_s) is then found to be close to the value proposed by Dohmen-Jassen and Hanes (2002), i.e., c_b ? 0.06 instead of 0.08, but its value is sensitive to the coefficient n specifying the hindered settling velocity.

Figure 52(b) plots the same concentration profile as in Figure 52(a) represented emphasizing the three different layers where the bed is fixed and moves with large concentration (sheet flow), where suspension occurs. Thus, it is seen that estimation of the suspended concentration profile may be done with simple formulas. A fitted exponential profile and fitted parabolic logarithmic profile were added. It appears that both profiles can yield a correct estimate of the suspended sediment concentration profile using a reference concentration smaller than c_b. On the other hand, these formulas exhibit limitations close to the bed and thus appear to be sensitive to choice of the reference concentration.

As Van Rijn (1993) found, similar sediment diffusivity profiles were observed for a rippled bed. The thickness d_m is then assumed to be on the order of the ripple height instead of the thickness of the sheet-flow layer. The same kind of suspended sediment profile should be obtained, whereas in the moving mixing layer, larger and smaller concentration should be observed on the crest and the trough of a ripple, respectively (Figure 53). The sediment diffusivity due to the ripples is large close to the bed because of ripple-generated eddies, but does not increase steeply over the depth because the eddies dissolve traveling upwards.

---

(a)
(b)

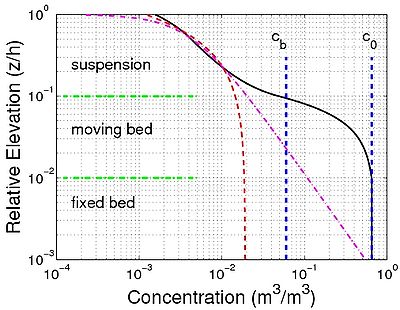Figure 52. (a) Characteristic sediment diffusion profile (Equation 142) and induced sediment concentration profile, and (b) division of induced concentration profile to
different layers and application of an exponential and parabolic
logarithmic profile to estimate suspended load.

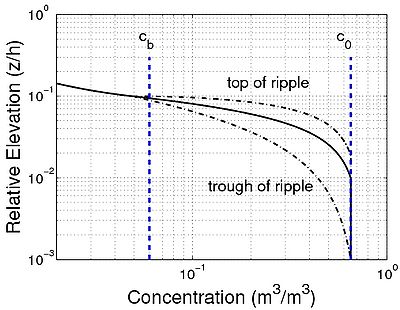
Figure 53. Schematic representation of sediment concentration within moving mixing layer for rippled bed.

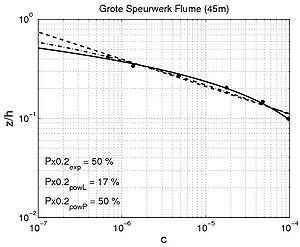
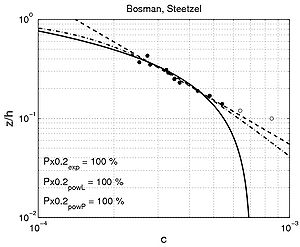
Shape of concentration profile As for a steady current, concentration profiles described by power-law and exponential equations were fitted to the measurements. For a power-law profile, a linear and a parabolic variation in sediment diffusivity over depth were investigated. Some typical examples of fitted profiles are presented in Figures 54, 55, and 56 for each of the data sets. Table 20 lists the percentage of sediment concentration predicted within a range of 20 percent error for the different data sets presented (pred_20,meas, pred_20,powL, and pred_20,pow denote the fitting of the exponential-law and the linear and parabolic power-laws, respectively). These calculations were also performed for sediment concentration data taken at locations closer to the bed (z < h/10) or in the upper layer (z > h/10), where the velocity is approximately constant.

---

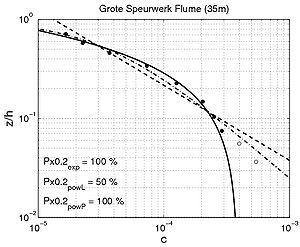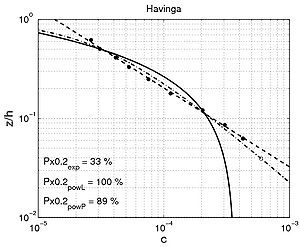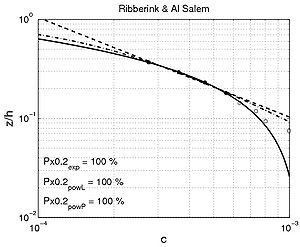
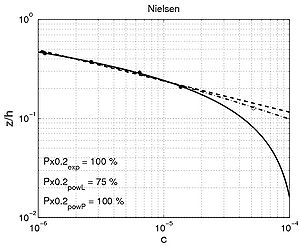
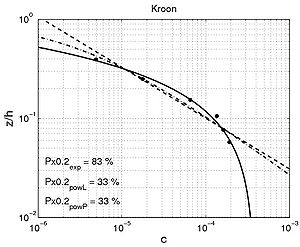
Figure 54. Examples of comparison between predicted concentration using fitted exponential profile (solid line) and power-law profiles (dashed and dashed-dotted line) and
measured concentration for interaction between nonbreaking waves and current (data from wave flumes, water tunnels, and basins).

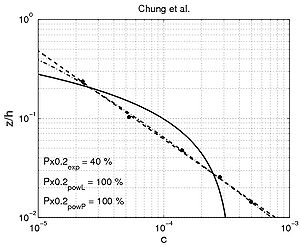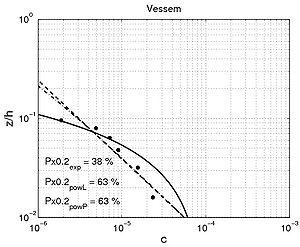
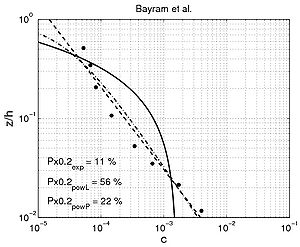
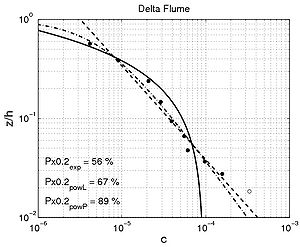
Figure 55. Examples of comparison between predicted concentration using fitted exponential profile (solid line) and power-law profiles (dashed and dashed-dotted line) and measured concentration for interaction between nonbreaking waves and current (data from large scale facilities and field measurements).

	(a)	(b)
(1)
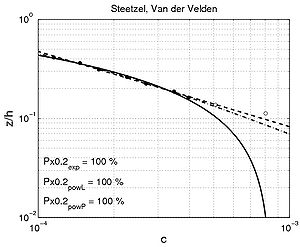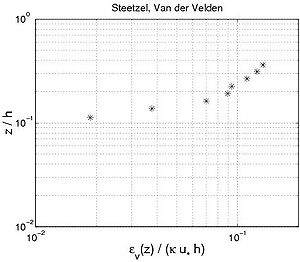(2)
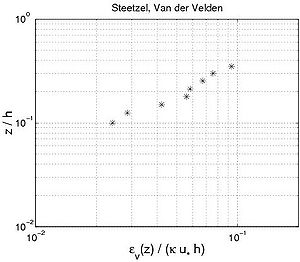(3)
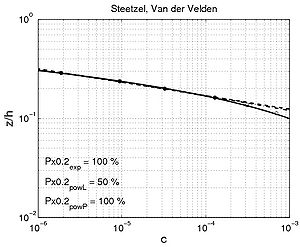(4)

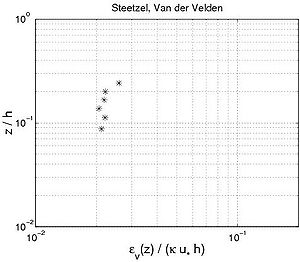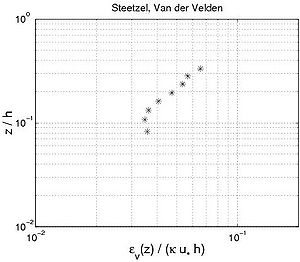
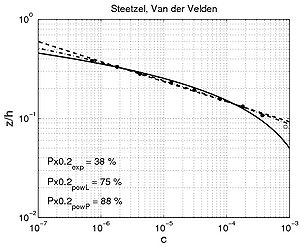
Figure 56. Examples of (a) concentration profiles, and (b) corresponding sediment diffusivity profiles, using data from Steetzel (1984) and Van der Velden (1986).

Table 20. Percentage of predicted sediment concentrations within +/- 20 percent of measured values using exponential-law or power-law (linear and parabolic
profiles for ?_w'''') profiles for studied data sets.

Author(s)	Exponential (%)				Linear Power (%)	Parabolic Power (%)
	z	z '< '''h'''/10'	z	z '< '''h'''/10'	z	z '< '''h'''/10'
Bosman, Steetzel	30.5	4.6	57.9	14.3	46.5	10.0
Nielsen	35.8	15.3	54.7	23.0	53.6	22.1
Steetzel, Van der Velden	62.5	15.0	69.2	14.4	72.5	15.0
Kroon	66.3	38.9	75.0	48.1	80.0	50.0
Havinga	54.0	24.9	94.9	44.1	88.8	44.6
Ribberink & Al Salem	57.6	30.4	78.3	42.7	81.2	44.7
Chung et al.	51.5	34.7	90.1	53.5	87.1	55.4
Vessem	50.8	41.1	69.4	53.2	69.9	54.3
Grote Speurwerk (35 m)	55.7	28.0	38.9	21.0	53.6	27.7
Grote Speurwerk (45 m)	73.9	27.5	68.3	21.8	75.9	25.0
Deltaflume	18.4	13.8	57.0	29.7	49.1	28.0
Bayram et al.	29.3	15.9	67.8	42.7	61.5	38.9
Total	53.2	21.7	65.8	26.9	67.2	27.7

Fitting of the three theoretical profiles gives poorer agreement with the data (especially for the exponential profile) compared to the steady flow situation. Less than 60 percent of the data are predicted within a factor of 1.2 by an exponential profile, and less than 70 percent by a fitted power-law profile. These figures drop to below 30 percent for data close to the bed (where z/h < 0.1). Some explanations may be suggested for the increased discrepancy:

• Several data sets correspond to field experiments where measurements are not as easy to make as in the laboratory, and so the variability in general is larger (Nielsen (1984), "Vessem," and Bayram et al. (2001) data sets).
• Contrary to the steady flow data, it appears for several data sets that two layers occur for suspension. The layer closest to the bed (defined as the "moving mixing layer" by Van Rijn 1989) corresponds to much smaller sediment diffusivity compared to the upper layer, and it may sometimes include bed-load transport.
• For the specific case of fitting an exponential profile, if two layers appear, fitting to all the data typically presents difficulty over some range of values (Figure 54: Bosman (1982), Steetzel (1985), and Figure 55: "Vessem" (Van Rijn et al. 2001), Bayram et al. (2001), and Delta Flume).
• Few measurements were made close to the mean water surface (generally limited to the trough level of the waves). It is thus difficult to observe the decrease of the sediment diffusivity as was done for a steady current.

Figure 56 plots four different concentration profiles and the sediment diffusivity profiles typically observed using the Steetzel (1985) and Van der Velden (1986) data sets shown (small water-tunnel with d₅₀ = 0.22 mm, h = 0.4 m, U_c = 0 m/sec). The input parameters are listed in Table 21. Some of the experiments correspond to nonphysical waves, because the steepness ?_w would be greater than 0.14.

Table 21. Input parameters for four study cases in Figure 56.

Case	Uw '''''''(m/sec)	TW '''''''(sec)	?w	Hr '(m)'	Lr '(m)'
1	0.75	1.0	0.324	0.020	0.300
2	0.50	1.5	0.090	0.013	0.080
3	0.30	1.5	0.054	0.013	0.105
4	0.50	2.0	0.059	0.023	0.130

It may be seen in Figure 56 that the concentration measurements inside the moving mixing layer largely influence the profile fitting. The results are affected by the difference between the value of the sediment diffusivity inside the moving mixing layer ?_w,bed and at z_w (maximum value ?_w,max). Usually, the difference z_w - d_m is small, and corresponds to a transition zone. Up to z_w, the sediment diffusivity is a weak function of z/h such that both the exponential and power-law fits yield acceptable results.

• Figure 56(1) represents a situation where no data points were available inside the moving mixing layer; the difference between the sediment diffusivity inside the mixing layer and its maximum value is large (?_w,bed/?_w,max < 0.2). The two layers can be clearly observed in the concentration profile. A fitted exponential profile induces a large underestimation of the concentration when z/h < 0.1. The orbital wave velocity is large compared to the wave period (?_w > 0.14).
• Figure 56(2) represents a situation where some data points were obtained inside the moving mixing layer; the difference between the sediment diffusivity inside the mixing layer and its maximum value is not as large as for Figure 56(1) (?_w,bed/?_w,max ? 0.3-0.4). The two layers cannot be observed in the concentration profile. A fitted exponential profile produces a large underestimation of the concentration for z/h < 0.1. On the other hand, a power-law profile gives a good approximation of the concentration profile.
• Figure 56(3) represents a situation where some data points were obtained inside the moving mixing layer; the difference between the sediment diffusivity inside the mixing layer and its maximum value is small (?_w,bed/?_w,max > 0.4). The two layers cannot be observed in the concentration profile. The fitted exponential profile seems to yield a good approximation of the concentration profile, and if a power-law profile yields somewhat better results.
• Figure 56(4) represents a situation where the sediment diffusivity is approximately constant over the depth (?_w,bed ? ?_w,max). A fitted exponential profile gives the best representation of the concentration profile.

It appears that the ratio ?_w,max/?_wbed (and more specifically ?_w,max) is proportional to the wave orbital velocity U_w and inversely proportional to the wave period T_w, which means proportional to the wave steepness ?_w. For realistic waves where ?_w < 0.14, the exponential profile yields an accurate approximation of the sediment concentration profile.

Similar observations were made for the Bosman (1982) and Steetzel (1984), "Grote Speurwerk (35 m), Vessem, Delta Flume" (Van Rijn et al. 2001), and Ribberink and Al Salem (1994) data sets.

Following these results and what was obtained for a mean current, only the mean sediment diffusivity over the water depth (exponential concentration profile) is examined in the following.

Relationships for mean sediment diffusivity under waves Because the shear stress cannot be calculated from measurements, but must be estimated, large uncertainties appear in the calculation of the ratio ?_w/(?hu_*w), especially because of the influeence of bed forms. Indeed, for most of the cases with low and mid-energy wave dissipation, ripples occur and strongly influence the suspended sediment profile. Furthermore, in most of the previous studies, semi-empirical relationships proposed for ?_w were typically not based on the orbital motion due to waves.

Dally and Dean (1984) assumed that the classical expression given by Rouse (1938) may be applicable, assuming a parabolic profile and using its mean value over the depth (see "Sediment diffusivity due to steady current" section):

\begin{equation} \tag{143} \varepsilon_{w,E} =\frac{1}{6}\kappa u_{*w} h \end{equation}

Skafel and Krishnappan (1984) employed a simple model to estimate the suspended sediment distribution assuming an exponential sediment suspension profile. The mean sediment diffusion ?_w was evaluated by the following expression:

\begin{equation} \tag{144} \varepsilon_{w,E} =\beta_w A_w u_{*w} \end{equation}

where ß_w is a dimensionless diffusion coefficient (ß_w ? 0.1). Using their own data set (small wave flume with glass beads, s = 2.5 and d₅₀ = 0.15 mm), and assuming k_s = H_r for the calculation of u_*w, they found the following relationship for ß_w:

\begin{equation}\tag{145} \beta_w = 8.7 \left( \frac{d_{50} u_{*w}}{v} \right)^{-2.2} \end{equation}

Van Rijn (1989) proposed empirical expressions for the minimum and maximum values of the sediment diffusivity (Equation 142):

\begin{equation}\tag{146} \varepsilon_{w,bed} = 0.004 d_* U_w \delta_m \end{equation}

\begin{equation}\tag{147} \varepsilon_{w,max} = 0.035 \frac{H_s h}{T_p} \end{equation}

where $H_s$ and $T_p$ are the significant wave height and the peak wave period, respectively.

Kosyan (1985) developed a semi-empirical model to estimate the diffusion coefficient distribution over the water depth. It appeared that the main component is produced by the orbital motion, and the distribution was found to be, using small-amplitude wave theory,

\begin{equation}\tag{148}

 \varepsilon_w = \frac{\pi H_w^2}{2\sqrt{2}T_w}\frac{\text{sinh}^2 kz}{\text{sinh}^2 kh}

\end{equation}

where $H_w$ is the wave height. The mean value over the depth is:

\begin{equation}\tag{149}

 \varepsilon_{e,E} = \frac{\pi H_w^2 h}{4\sqrt{2} T_w }\left( \frac{\text{sinh}2kh}{2kh}-1 \right) \approx \frac{8\pi^3 U_w^3 h^3}{3\sqrt{2} g^2 T_w^3}

\end{equation}

For waves only and a rippled bed, Nielsen (1992, pp. 215-217) observed that an exponential profile describes the concentration profile well. He found that the mean sediment diffusivity is closely related to the ripple height $H_r$ for sharp-crested ripples and suggested:

\begin{equation}\tag{150} \varepsilon_{w,E} = 0.075 U_w H_r \text{ for }\frac{U_w}{W_s}\le 18 \end{equation}

\begin{equation}\tag{151} \qquad = 1.4 W_s H_r \text{ for }\frac{U_w}{W_s}<18 \end{equation}

Analyzing the data set previously presented (Table 19), where waves are not breaking and the mean current is negligible ($\left|{{U}_{c}}\right|<0.05$), a comparison was made between the different formulas studied and the data. The percentage of predicted values within a factor of 1.5, 2, and 5 deviation (denoted by Px1.5, Px2, and Px5, respectively) as well as the mean value and the standard deviation of the ratio f(?_w,E) = log (?_w,pred/?_w,meas) are presented in Table 22 .

Of the studied formulas, the one proposed by Dally and Dean (1984), who assumed that the Rouse expression could be used, gives the least scatter, even if the formula in general overestimates the diffusivity. This expression may be correct, but the Schmidt number appears to be much smaller than 1. The more complex formulas introduced by Skafel and Krishnappan (1984) and Nielsen (1992, pp. 215-217) yield better overall fit (especially the Nielsen formula), but also larger scatter.

Table 22. Predictive skill of different formulas for sediment diffusivity for waves only.

Author(s)	Px'''1.5 (%)	Px'''2 (%)	Px'''5 (%)	Mean('''f'''('''cR))	Std('''f'''('''cR))
Dally & Dean	3	10	51	0.69	0.29
Skafel & Krishnappan	3	7	35	-0.68	0.76
Kos'yan	12	17	49	-0.35	0.94
Van Rijn	23	38	76	0.29	0.52
Nielsen	33	60	89	-0.24	0.38
Equation 152	58	86	99	-0.02	0.22
Equation 153	46	68	98	0.09	0.29
Equation 154	45	69	100	0.09	0.28

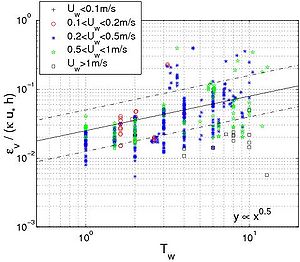
New formula for mean sediment diffusivity due to waves Assuming that the Rouse expression can be adopted, the ratio ?_w,E/(?hu_*w) was plotted against the main parameters. As observed by Nielsen (1992), this ratio is related to U_w/W_s and to wave period (Figure 57). Based on the studied data set, a new empirical equation is proposed:

\begin{equation}\tag{152}

 \varepsilon_{w,E} = 4 10^{-3}
 \left( \frac{g^{2/3}T_w}{\nu^{1/3}} \right)^{0.5}
 \left( \frac{U_w}{W_s} \right)^{-0.5}
 \kappa u_{*w} h

\end{equation}

(a)	(b)

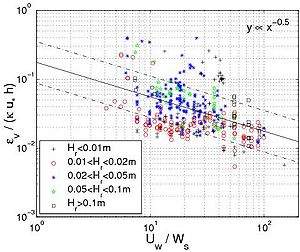Figure 57. Dimensionless sediment diffusivity ?_w,E/(?'''hu*w) versus (a) wave period,
and (b) ratio '''U_w/'''Ws.

Equation 152 presents the best results among the studied formulas. More than 85 percent of the data points are correctly predicted within a factor 2 and nearly 100 percent within a factor 5. Also, Figure 58 shows that the results do not depend on the data set.

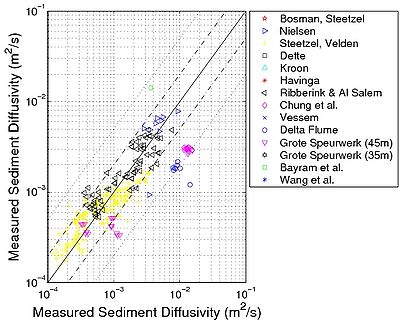
Figure 58. Vertical sediment diffusivity ?_w,E 'estimated from data compiled
versus ?w,E 'calculated with Equation 152 ('''Uc '< 0.05).

However, following the study performed for the sediment diffusivity due to a current ("Sediment diffusivity under steady current" section), the correction factor (Schmidt number) may be taken to be a function of the ratio W_s/u_*w. The sediment diffusivity under waves may be written as an average over the wave period for an instantaneous sediment diffusivity, which for an exponential profile leads to ${{\varepsilon }_{w,E}}={{\sigma }_{w}}\kappa {{u}_{*w}}h/(3\pi )$, where s_w is the wave-related Schmidt number, and the coefficient 2/? corresponds to the time average of the function |sin|.

Plotting the dimensionless sediment diffusivity ?_w,E/(?hu_*w) versus the ratio W_s/u_*w (Figure 59), a trend appears similar to that observed for a current (Figure 48). Using the previous data sets, an expression for ?_w,E is proposed following the equation developed by Van Rijn (1984b) (Equation 122), which yields the following expression for the Schmidt number:

\begin{equation}\tag{153} \sigma_w = 0.2+2.5 \left( \frac{W_s}{u_{*w}} \right)^2 \end{equation}

To put forward a relationship that gives physically meaningful results for all conditions, it should be considered that if the ratio ${{W}_{s}}/{{u}_{*w}}\gg 1$, the Schmidt number should be equal to 1. Thus, a similar expression is proposed as for the steady current regarding the sediment diffusivity (Equation 136 and Figure 59):

\[\sigma_w = \left\{

 \begin{align}
  & 0.15 + 1.5 \sin^2 \left( \frac{\pi}{2}\frac{W_s}{u_{*w}} \right)
    \text{   if   }\frac{W_s}{u_{*w}}\le 1 \\
  & 1.0 + 0.65 \sin^2 \left( \frac{\pi}{2}\frac{u_{*w}}{W_s} \right)
    \text{     if   }\frac{W_s}{u_{*w}}>1 \\
 \end{align} \right. \qquad\qquad\text{(154)}\]

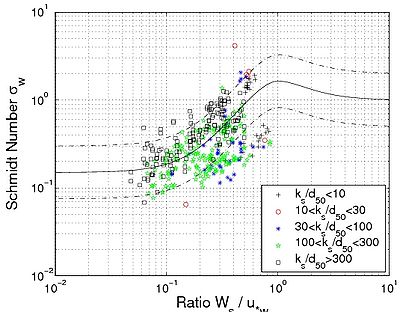
Figure 59. Estimated value of coefficient '''sw 'using Equation 154 as function
of ratio '''Ws/'''u*w 'with roughness ratio '''k_s/'''d50 'indicated.

The wave-induced Schmidt number (Equations 153 and 154) is often considerably smaller than that found for steady current (factor 2 or 3 smaller). However, because the friction velocity for waves is generally much larger than for a current, the mixing from waves is also much larger. As discussed, this mixing may decrease the Schmidt number. The oscillatory velocities at the bottom may also affect the Schmidt number, and the results obtained using these formulas are not as good as the results obtained using Equation 152. An improvement, however, is obtained in agreement with the data compared to the other studied formulas: 45 percent of the data are correctly predicted with a permitted error of a factor 1.5, and 69 percent with a permitted error of a factor 2.

There seems to be a relationship between s_w and the roughness ratio k_s/d₅₀ (Figure 59). Because this roughness ratio (and the total shear stress) is calculated using empirical formulas and not estimated directly from the measusrements (contrary to the data for current only), the relationship between s_w and k_s/d₅₀ exhibits larger scatter. Another explanation could be that the proposed Schmidt number does not take into account a possible effect of wave period as observed in Equation 152.

Interaction between waves and current If waves and current interact, the most straight-forward approach would be to add the two values obtained from current only (Equations 134 and 136) and waves only (Equation 154), i.e., ?_cw,E = ?_w,E + ?_c,E. However, it may be noted that this summation does not present correct results compared to the measurements (Figure 60). Indeed, the larger the ratio U_c/U_w is, the larger the overestimation of the measurements. On the other hand, using the sediment diffusivity for waves only produces a large underestimation (see Table 23). The overestimation obtained using a summation approach may also be attributed to the calculation of the total shear velocity including the current. Indeed, for the calculation of u_*c, the roughness was assumed to be equal to the wave-induced Nikuradse roughness (a function of the wave-induced ripples), even if the direction of the current may affect this value.

Van Rijn (1989) proposed use of a mean quadratic value of the current-related and wave-related sediment diffusivity:

\begin{equation}\tag{155} \varepsilon_{cw} = \sqrt{\varepsilon_c^2 + \varepsilon_w^2} \end{equation}

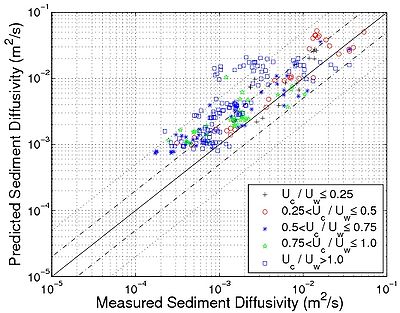
'Figure 60. Estimation of sediment diffusivity '''?cw 'by adding current- and wave-related sediment diffusivity as function of parameter '''W_s/'''u*w 'with ratio '''Uc/Uw 'emphasized.

Table 23. Prediction of sediment diffusivity for wave and current interaction (for different calculations of ?_{cw''''''','''E''''}, Equations 136 and 154 are used for obtaining ?_{c''''''','''''''E''} 'and ?w''''''','''E'''_', respectively).

Equation	Px'''2 (%)	Px'''5 (%)	Mean('''f'''('''cR))	Std('''f'''('''cR))
Dally & Dean (1984)	55	89	0.20	0.39
Van Rijn (1989)	37	83	0.18	0.50
Nielsen (1992)	0	1	-1.68	0.80
${{\varepsilon }_{cw,E}}={{\varepsilon }_{c,E}}+{{\varepsilon }_{w,E}}$	51	86	0.29	0.36
${{\varepsilon }_{cw,E}}={{\varepsilon }_{w,E}}$	49	94	-0.22	0.34
${{\varepsilon }_{cw,E}}={\sqrt {\varepsilon _{c,E}^{2}+\varepsilon _{w,E}^{2}}}$	58	88	0.18	0.38
${{\varepsilon }_{cw,E}}={{X}_{v}}{{\varepsilon }_{c,E}}+\left(1-{{X}_{v}}\right){{\varepsilon }_{w,E}}$	60	91	0.02	0.40
${{\varepsilon }_{cw,E}}={{\varepsilon }_{c}}_{,E}+{{\varepsilon }_{w,E}}$ using ${{\sigma }_{c}}={{\sigma }_{w}}={{\sigma }_{cw}}$ (Equation 156)	65	92	0.09	0.38

Thus, a correction factor may be applied to compute the diffusivity for waves and current combined. Using the approach of Grant and Madsen (1979) for the computation of wave-current friction factors, i.e., ?_cw,E = (1   X_v) ?_w,E + X_v ?_c,E with ${{X}_{v}}=\left|{{U}_{c}}\right|/\left(\left|{{U}_{c}}\right|+{{U}_{w}}\right)$, improved results are expected (Table 23). However, it seems that the effect of the current on the sediment diffusivity is suppressed by the waves. Indeed, the Grant and Madsen (1979) method presents good results mainly if U_c/U_w > 0.5. For U_c/U_w < 0.5, it tends to underestimate ?_cw,E.

This overestimation may be attributable to the Schmidt number perhaps being the same for a current and for waves. A more physical description of the wave and current interaction should be based on a unique Schmidt number, calculated as an empirical weighted value between s_c and s_w. According to the data, the effect of the waves seems to be larger, and the following relationship is thus proposed:

\begin{equation}\tag{156} \sigma_{cw} = Y \sigma_c + (1-Y) \sigma_w \end{equation}

where Y = ?_c/(?_{c +} ?_w). The scatter may be due to uncertainties in the estimation of the current- and wave-induced shear stress.

In Figure 61, the vertical sediment diffusivity ?_cw,E estimated from the compiled data is plotted versus ?_cw,E calculated with Equation 156 for wave and current interaction (U_c > 0.05). It seems that the scatter is mainly associated with the Vessem and the Chung et al. (2000) data, which are often overestimated, and with the Bayram et al. (2001) data, which are underestimated.

Effect of breaking waves on sediment diffusivity

The vertical distribution of suspended sediment in the surf zone is controlled by the downward settling of sediment particles and the upward mixing of particles due to turbulent diffusion and wave advection. The dominant mechanism for generation of turbulence outside the surf zone is bottom friction, whereas inside the surf zone turbulence is generated both at the seabed by friction and near the water surface by wave breaking. Therefore, large concentrations of sediment can be suspended throughout the water column (Yu et al. 1993; Ogston and Sternberg 2002).

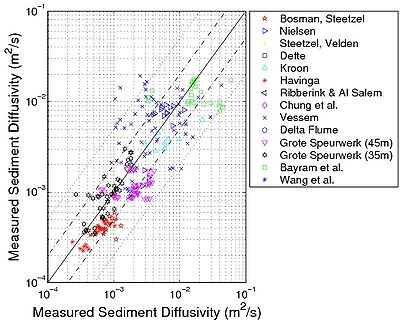
Figure 61. Vertical sediment diffusivity ?_cw''','''E 'estimated from compiled data versus ?cw,E 'calculated with Equation 156 for wave and current interaction ('''Uc '> 0.05).

Extension of sediment diffusion expression In a study on infilling of navigation channels, Kraus and Larson (2001) employed an exponential concentration profile to estimate the suspended load transport. Wave breaking was assumed to be the main mechanism for the vertical mixing, yielding a concentration profile according to Equation 123 with:

\begin{equation}\tag{157}

\varepsilon = \varepsilon_b = k_b \left( \frac{D_b}{\rho} \right)^{1/3} h

\end{equation}

where $k_b$ is an empirical constant, and $D_b$ is the energy dissipation due to wave breaking. The expression for $\varepsilon$ produces a constant eddy viscosity over the water depth.

A general expression for $\varepsilon$ should include mixing associated with turbulence from bottom friction and with wave breaking. Also, bottom friction should encompass effects of waves and currents, acting separately or in combination. By exploring the relationship between energy dissipation and shear stress in the bottom boundary layer, the mixing from the bottom turbulence may be expressed through the energy dissipation, which in turn means that this mixing can be combined with the mixing due to breaker-induced turbulence in a straightforward manner. The energy dissipation in the bottom boundary layer under a current may be written:

\begin{equation}\tag{158} D_c = \tau_c \ u_{*c} \end{equation}

where $u_{*c}$ is the shear velocity due to current only. This expression makes it possible to replace the shear velocity in the eddy viscosity with the energy dissipation.

Equation 158 deviates from the standard way of defining the dissipation due to a current, which should be expressed as the product between a force and a velocity (the mean velocity $U_c$ is generally used instead of the shear velocity $u_{*c}$). However, using $u_{*c}$ instead of $U_c$ yields the same result as the classical mixing length approach:

\begin{equation}\tag{159}

 \varepsilon_c = k_c \left( \frac{D_c}{\rho} \right)^{1/3}\quad h=k_c \left( \frac{\tau_c u_{*c}}{\rho} \right)^{1/3}\quad h

\end{equation}

\begin{equation}\tag{160} = k_c u_{*c} h \end{equation}

Similarly, the energy dissipation in the bottom boundary layer because of the wave motion may be expressed as:

\begin{equation}\tag{161} D_w = \tau_w u_{*w} \end{equation}

where $u_{*w}$ is the shear velocity from waves only. The sediment diffusivity due to waves may thus be written:

\begin{equation}\tag{162} \varepsilon = k_w \left( \frac{D_w}{\rho} \right)^{1/3} h\end{equation}

\begin{equation}\tag{163} = k_w u_{*w} h\end{equation}

To employ a general formula for the sediment diffusion, it is natural to assume that:

\begin{equation}\tag{164} \varepsilon = \left( \frac{D}{\rho} \right)^{1/3} h \end{equation}

where D is the total effective dissipation:

\begin{equation}\tag{165} D=k_b^3 D_b + k_c^3 D_c + k_w^3 D_w \end{equation}

in which the energy dissipation from wave breaking ($D_b$), from bottom friction from a current ($D_c$), and from waves ($D_w$), ($k_b$, $k_c$, and $k_w$ are coefficients). The coefficient $k_b$ mainly corresponds to an efficiency factor, whereas $k_c$ and $k_w$ are related to the Schmidt number. Typically, $D_b > D_w > D_c$ and, in many cases, only the largest dissipation needs to be considered. Still, the formula for $\varepsilon$ is simplified because the mixing does not vary through the water column.

Using Equation 134 together with Equation 136 and Equation 154, it is found that:

\[k_c = \frac{\kappa \sigma_c}{6} = \frac{\kappa}{6} \left\{

  \begin{align}
    & 0.4+3.5 \sin^2 \left( \frac{\pi}{2} \frac{W_s}{u_{*c}} \right)
      \text{   if   } \frac{W_s}{u_{*c}} \le 1 \\
    & 1.0+2.9 \sin^2 \left( \frac{\pi}{2} \frac{u_{*c}}{W_s} \right)
      \text{   if   } \frac{W_s}{u_{*c}} \gt 1 \\
  \end{align} \right.\qquad\qquad\text{(166)}\]

\[k_w = \frac{\kappa \sigma_w}{3 \pi} = \frac{\kappa}{3 \pi} \left\{

  \begin{align}
    & 0.15+1.5 \sin^2 \left( \frac{\pi}{2} \frac{W_s}{u_{*w}} \right)
      \text{   if   } \frac{W_s}{u_{*w}} \le 1 \\
    & 1.0+0.65 \sin^2 \left( \frac{\pi}{2} \frac{u_{*w}}{W_s} \right)
      \text{   if   } \frac{W_s}{u_{*w}} \gt 1 \\
  \end{align} \right.\qquad\qquad\text{(167)}\]