Circular Basin: Difference between revisions
m 1 revision: Import from Fault |
m →Problem |
||
| Line 3: | Line 3: | ||
=Problem= | =Problem= | ||
Dupont (2001) presented an analytical solution for a closed circular domain on an f-plane with a linear bottom friction. The governing equations are | Dupont (2001) presented an analytical solution for a closed circular domain on an f-plane with a linear bottom friction. The governing equations are | ||
\begin{equation} \tag{1} | |||
\frac{\partial H U}{\partial x} + \frac{\partial H V}{\partial y} = 0 | |||
\end{equation} | |||
\begin{equation} \tag{2} | |||
-f_c V + g \frac{\partial \eta}{\partial x} = \kappa U + \frac{W y}{R H} | |||
\end{equation} | |||
\begin{equation} \tag{3} | |||
<math> f_c U + g \frac{\partial \eta}{\partial y} = \kappa V | |||
\end{equation} | |||
where <math>U</math> and <math>V</math> are the depth-averaged current velocities in the <math>x</math> and <math>y</math> directions respectively, <math>g</math> is the gravitational constant, <math>\eta</math> is the water surface elevation with respect to mean sea level, <math>\kappa</math> is a linear bottom friction coefficient, <math>R</math> is the radius of the domain, <math>H</math> is the water depth, and <math>W</math> is a constant equal to the gradient of the wind forcing. | where <math>U</math> and <math>V</math> are the depth-averaged current velocities in the <math>x</math> and <math>y</math> directions respectively, <math>g</math> is the gravitational constant, <math>\eta</math> is the water surface elevation with respect to mean sea level, <math>\kappa</math> is a linear bottom friction coefficient, <math>R</math> is the radius of the domain, <math>H</math> is the water depth, and <math>W</math> is a constant equal to the gradient of the wind forcing. | ||
Revision as of 14:31, 16 July 2012
UNDER CONSTRUCTION
Problem
Dupont (2001) presented an analytical solution for a closed circular domain on an f-plane with a linear bottom friction. The governing equations are \begin{equation} \tag{1}
\frac{\partial H U}{\partial x} + \frac{\partial H V}{\partial y} = 0
\end{equation}
\begin{equation} \tag{2}
-f_c V + g \frac{\partial \eta}{\partial x} = \kappa U + \frac{W y}{R H}
\end{equation}
\begin{equation} \tag{3}
Failed to parse (syntax error): {\displaystyle f_c U + g \frac{\partial \eta}{\partial y} = \kappa V \end{equation} where <math>U}
and are the depth-averaged current velocities in the and directions respectively, is the gravitational constant, is the water surface elevation with respect to mean sea level, is a linear bottom friction coefficient, is the radius of the domain, is the water depth, and is a constant equal to the gradient of the wind forcing.
Solution
The analytical solution for water surface elevation solution is given by
| (1) |
The current velocities are independent of the Coriolis parameter and are given by
| (3) |
| (4) |
Setup

The model is run to steady state from zero current and water level initial conditions with , , and . Table 1 shows the general settings used for CMS-Flow. Figure 1 shows the computational grid with 5 levels of refinement from 2000 m to 125 m.
Table 1. General Settings for Wind-driven flow in a circular basin
| Parameter | Value |
| Time step | 3600 s |
| Simulation Duration | 72 hrs |
| Ramp Period | 24 hrs |
| Initial Water Depth | 100 m |
| Mixing Terms | Off |
| Wall Friction | Off |
| Linear Bottom Friction Coefficient | 0.001 |
Results
No Coriolis
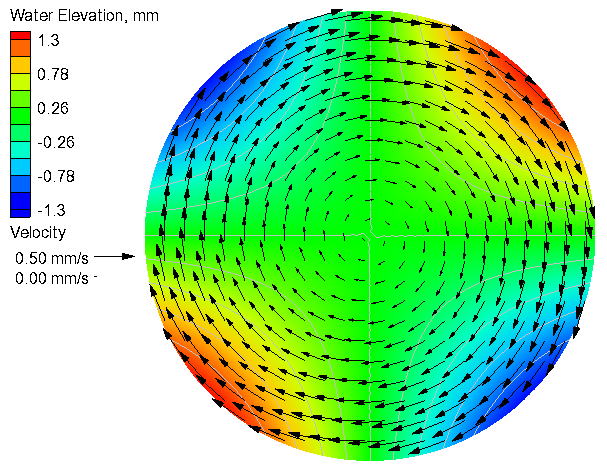
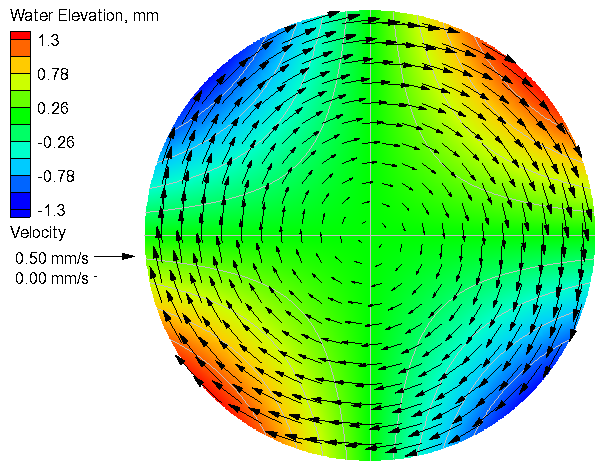
Table 2. Goodness of fit statistics for the current velocity and water level
| Variable | NRMSE, % | NMAE, % | R^2 | Bias |
| U-Velocity | 2.52 | 0.37 | 0.999 | -8.5e-8 m/s |
| V-Velocity | 2.53 | 0.38 | 0.999 | 7.26e-8 m/s |
| Water Level | 0.03 | 0.02 | 0.999 | -3.5e-7 m |
- For a definition of the goodness of fit statistics see Goodness of fit statistics.
With Coriolis

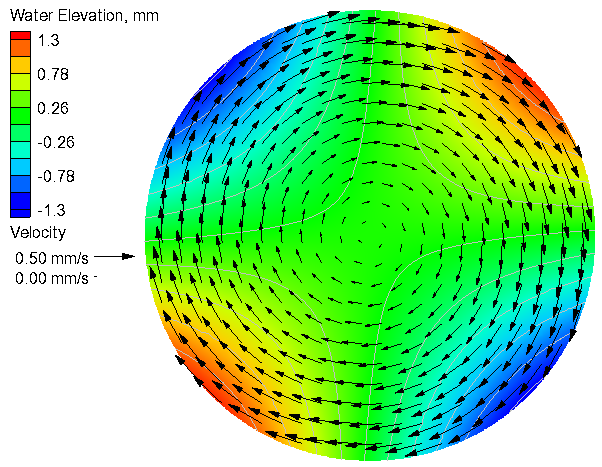
Table 3. Goodness of fit statistics for the current velocity and water level
| Variable | RRMSE, % | RMAE, % | R^2 | Bias |
| U-Velocity | 2.53 | 0.37 | 0.999 | -8.5e-8 m/s |
| V-Velocity | 2.56 | 0.37 | 0.999 | 6.5e-8 m/s |
| Water Level | 0.03 | 0.02 | 0.999 | -3.0e-7 m |
References
- Dupont, F., 2001. Comparison of numerical methods for modelling ocean circulation in basins with irregular coasts. Ph.D. thesis, McGill University, Montreal.