CMS-Flow:Hydro Eqs

Continuity and Momentum Equations

Phillips (1977), Mei (1983), and Svendsen (2006) provide a detailed deri-vation of the depth-integrated and wave-averaged hydrodynamic equa-tions. Here, only variable definitions are provided and derivations may be obtained from the preceding references. The instantaneous current velocity u_i is split into:

$u_{i}={\bar {u_{i}}}+{\tilde {u_{i}}}+u_{i}^{'}$

(1)

in which

${\bar {u_{i}}}$ = current (wave-averaged) velocity [m/s]

${\tilde {u_{i}}}$ = wave (oscillatory) velocity with wave-average ${\bar {\tilde {u_{i}}}}=0[m/s]$

$u_{i}^{'}$ = turbulent fluctuation with ensemble average $\langle u_{i}^{'}\rangle$ = 0 and wave average ${\bar {u_{i}^{'}}}$ = 0 [m/s]

The wave-averaged total volume flux is defined as

2

({{{2}}})

where

$h$ = wave-averaged water depth $h={\bar {\eta }}-z_{b}$ [m]

$V_{i}$ = total mean mass flux velocity or simply total flux velocity for short [m/s]

$u_{i}$ = instantaneous current velocity [m/s]

$\eta$ = instantaneous water level with respect to the Still Water Level (SWL) [m]

$z_{b}$ = bed elevation with respect to the SWL [m]

For simplicity in the notation, the over bar in subsequent wave-averaged variables is omitted. The total flux velocity is also referred to as the mean transport velocity (Phillips 1977) and mass transport velocity (Mei 1983). The current volume flux is defined as

$hU_{i}=\int _{z}^{\eta }{\bar {u_{i}}}dz$

(3)

where $U_{i}$ is the depth-averaged current velocity. Similarly, the wave volume flux is defined as by

$Q_{wi}=hU_{wi}={\bar {\int {\tilde {u_{i}}}dz}}$

(4)

where $U_{wi}$ is the depth-averaged wave flux velocity [m/s], and $\eta _{t}$ = wave trough elevation [m]. Therefore the total flux velocity may be written as

$V_{i}=U_{i}+U_{wi}$

(5)

On the basis of the above definitions, and assuming depth-uniform cur-rents, the general depth-integrated and wave-averaged continuity and momentum equations may be written as (Phillips 1977; Mei 1983; Svendsen 2006)

${\frac {\partial h}{\partial t}}+{\frac {\partial (hV_{j})}{\partial x_{j}}}=S_{M}$

(6)

${\frac {\partial (hV_{i})}{\partial t}}+{\frac {\partial (hV_{j}V_{i})}{\partial x_{j}}}-\varepsilon _{ij}f_{c}hV_{j}=-gh{\frac {\partial {\bar {\eta }}}{\partial x_{i}}}-{\frac {h}{\rho }}{\frac {\partial p_{atm}}{\partial x_{i}}}+{\frac {\partial }{\partial x_{j}}}{\left(v_{t}h{\frac {\partial V_{i}}{\partial x_{j}}}\right)}-{\frac {1}{\rho }}{\frac {\partial }{\partial x_{j}}}\left(S_{ij}+R_{ij}-\rho hU_{wi}U_{wj}\right)+{\frac {\tau _{si}}{\rho }}-m_{b}{\frac {\tau _{bi}}{\rho }}$

(7)

where

$t$ = time[s]

$x_{j}$ = Cartesian coordinate in the $j^{tj}$ direction [m]

math>f_c</math> = Coriolis parameter [rad/s] $=2\Omega sin\phi$ where $\Omega =7.29x10^{-5}$ rad/s is the earth’s angular velocity of rotation and $\phi$ is the latitude in degrees

$h$ = wave-averaged total water depth $h=\zeta +{\bar {\eta }}$ [m]

${\bar {\eta }}=$ wave-averaged water surface elevation with respect to reference datum [m]

$S_{M}=$ water source/sink term due to precipitation, evaporation and structures (e.g. culverts) [m/s]

$V_{i}=$ total flux velocity defined as $V_{i}=U_{i}+U_{wi}$ [m/s]

$U_{i}=$ wave- and depth-averaged current velocity [m/s]

$U_{wi}=$ mean wave mass flux velocity or wave flux velocity for short [m/s]

$g=$ gravitational constant (~9.81 m/s²)

$p_{atm}=$ atmospheric pressure [Pa]

$\rho =$ water density (~1025 kg/m³)

$v_{t}=$ turbulent eddy viscosity [m²/s]

$\tau _{si}=$ wind surface stress [Pa]

$S_{ij}=$ wave radiation stress [Pa]

$R_{ij}=$ surface roller stress [Pa]

$m_{b}=$ bed slope coefficient [-]

$\tau _{bi}=$ combined wave and current mean bed shear stress [Pa]

The equations above are similar to those derived by Svendsen (2006), ex-cept for the inclusion of the water source/sink term in the continuity equation and the atmospheric pressure and surface roller terms in the momentum equation. It is also noted that the horizontal mixing term is formulated differently as a function of the total flux velocity, similar to the Generalized Lagrangian Mean (GLM) approach (Andrews and McIntyre 1978; Walstra et al. 2000). This approach is arguably more physically meaningful and also simplifies the discretization.

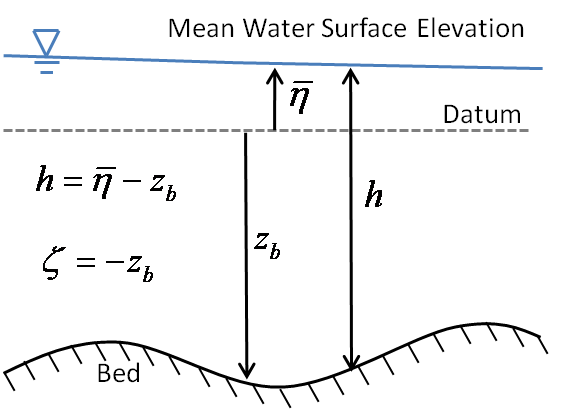
Figure 2-1 shows the vertical conventions used for mean water surface elevation and bed elevations. The arrows indicate the reference elevation for each variable. Note that the total water depth is always positive.

Figure 2-1 here.

Figure 2.1 Vertical conventions used for mean water surface elevation and bed elevations.

References

• Buttolph, A. M., Reed, C. W., Kraus, N. C., Ono, N., Larson, M., Camenen, B., Hanson, H.,Wamsley, T., and Zundel, A. K. (2006). “Two-dimensional depth-averaged circulation model CMS-M2D: Version 3.0, Report 2: Sediment transport and morphology change,” Tech. Rep. ERDC/CHL TR-06-9, U.S. Army Engineer Research and Development Center, Coastal and Hydraulic Engineering, Vicksburg, MS.
• Ferziger, J. H., and Peric, M. (1997). “Computational Methods for Fluid Dynamics”, Springer-Verlag, Berlin/New York, 226 p.
• Huynh-Thanh, S., and Temperville, A. (1991). “A numerical model of the rough turbulent boundary layer in combined wave and current interaction,” in Sand Transport in Rivers, Estuaries and the Sea, eds. R.L. Soulsby and R. Bettess, pp.93-100. Balkema, Rotterdam.
• Phillips, O.M. (1977) Dynamics of the upper ocean, Cambridge University Press.
• Rhie, T.M. and Chow, A. (1983). “Numerical study of the turbulent flow past an isolated airfoil with trailing-edge separation”. AIAA J., 21, 1525–1532.
• Saad, Y., (1993). “A flexible inner-outer preconditioned GMRES algorithm,” SIAM Journal Scientific Computing, 14, 461–469.
• Saad, Y., (1994). “ILUT: a dual threshold incomplete ILU factorization,” Numerical Linear Algebra with Applications, 1, 387-402.
• Saad, Y. and Schultz, M.H., (1986). “GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems,” SIAM Journal of Scientific and Statistical, Computing, 7, 856-869.
• Soulsby, R.L. (1995). “Bed shear-stresses due to combined waves and currents,” in Advanced in Coastal Morphodynamics, ed M.J.F Stive, H.J. de Vriend, J. Fredsoe, L. Hamm, R.L. Soulsby, C. Teisson, and J.C. Winterwerp, Delft Hydraulics, Netherlands. 4-20 to 4-23 pp.
• Svendsen, I.A. (2006). Introduction to nearshore hydrodynamics, Advanced Series on Ocean Engineering, 124, World Scientific Publishing, 722 p.
• Wu, W. (2004). “Depth-averaged 2-D numerical modeling of unsteady flow and nonuniform sediment transport in open channels,” Journal of Hydraulic Engineering, ASCE, 135(10) 1013-1024.
• Wu, W., Sánchez, A., and Mingliang, Z. (2011). “An implicit 2-D shallow water flow model on an unstructured quadtree rectangular grid,” Journal of Coastal Research, [In Press]
• Wu, W., Sánchez, A., and Mingliang, Z. (2010). “An implicit 2-D depth-averaged finite-volume model of flow and sediment transport in coastal waters,” Proceeding of the International Conference on Coastal Engineering, [In Press]
• Van Doormal, J.P. and Raithby, G.D., (1984). Enhancements of the SIMPLE method for predicting incompressible fluid flows. Num. Heat Transfer, 7, 147–163.
• Zhu, J. (1991). “A low-diffusive and oscillation-free convection scheme,”Communications in Applied Numerical Methods, 7, 225-232.
• Zwart, P. J., Raithby, G. D., Raw, M. J. (1998). “An integrated space-time finite volume method for moving boundary problems”, Numerical Heat Transfer, B34, 257.

---

Variable Index

Symbol	Description	Units
$t$	Time	sec
$h$	Total water depth $h=\zeta +\eta$	m
$\zeta$	Still water depth	m
$\eta$	Water surface elevation with respect to the still water elevation	m
$U_{j}$	Current velocity in the jth direction	m/sec
$S$	Sum of Precipitation and evaporation per unit area	m/sec
$g$	Gravitational constant	m/secsup2/sup
$\rho$	Water density	kg/msup3/sup
$p_{a}$	Atmospheric pressure	Pa
$\nu _{t}$	Turbulent eddy viscosity	msup2/sup/sec

---

Documentation Portal