Transcritical Bump

Test C1-Ex4: Transcritical Flow over a Bump

Purpose

This test case is used to assess the model performance in simulation of flow with mixed subcritical and supercritical regimes. Due to a steep change in bed elevation, the flow changes from subcritical to supercritical and back to subcritical. Because the bottom friction is not considered, an analytical solution is available for testing the water level calculations.

Problem

The one-dimensional problem (Caleffi et al. 2003) has a bed elevation given by

$z_{b}={\begin{array}{ll}0&x<8\\0.2-0.05\left(x-10\right)^{2}&8\leq x\leq 12\\0&x>12\\\end{array}}$

(4)

where $z_{b}$ is the bed elevation with respect to the still water level, and x is the horizontal distance. A constant flux boundary is specified at x=0 m and a constant water level boundary is specified at $x=12$m. The bed is frictionless. Table 10 shows a summary of the important hydrodynamic parameters for this case.

Table 10. Hydrodynamic parameters for the test case of flow over a bump

Parameter	Value
Flow discharge	0.18 m3/s
Downstream water depth	0.33 m
Bottom Friction	None

Model Setup

The implicit CMS-flow was applied with a computational domain of 25 ×0.3 m, and a constant grid spacing of 0.1 m (see Figure 11). A flux boundary condition was specified at the upstream boundary and a constant water level boundary condition was applied to the downstream boundary. The model was ramped from zero current velocity and a constant water level of 0.33 m over a period of 2.75 hr. For the implicit flow solver, an adaptive time step between 0.0781-20 s was applied. Table 11 summarizes the CMS setup. For the explicit flow solver, a constant time step of 0.01 s was applied. The computational times for the implicit and explicit solvers on a single 2.67 GHz processor were approximately 45 and 3.5 min, respectively.

Figure 11. CMS-Flow computational grid for the flow over a bump test case.

Table 11. CMS-Flow setup parameters for the flow over a bump test case.

Parameter	Value
Solution scheme	Implicit, Explicit
Time step	Implicit: 0.0781-20 s, Explicit: 0.015 s
Simulation duration	3 hr
Ramp duration	2.75 hr
Wall friction	0ff
Manning’s coefficient	0.0 s/m1/3

Results and Discussion

A comparison between the analytical and numerical solutions of water level is shown in Figure 12. The goodness-of-fit statistics summarized in Table 12 indicate that the mean calculated error is less than 3% and the squared correlation coefficient $R^{2}$ is 0.991. Both the implicit and explicit schemes produce accurate results with NMAE values equal to 1.28% and 1.30% respectively. The location of the hydraulic jump is captured well with both the implicit and explicit schemes. In the case of the implicit scheme, the water level downstream of the bump is slightly underpredicted and results in with a slight negative bias shown in Table 12. The explicit scheme slightly overestimates the water level immediately downstream of the hydraulic jump and also slightly underestimates the water levels upstream of the bump. The overall bias of the explicit scheme water levels is negative. It is noted that although the implicit solution scheme is not designed or intended for flows with sharp discontinuities, the CMS has the capability to produce accurate results.

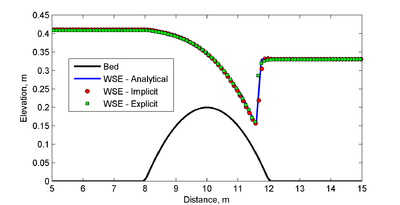Figure 12. Comparison of analytical and calculated water surface elevations for the flow over a bump test case. The bed elevation is also shown for reference.

Table 12. Water level goodness-of-fit statistics* for the flow over a bump test case

Statistic	Implicit	Explicit
NRMSE, %	2.86	3.31
NMAE, %	1.28	1.30
$R^{2}$	0.991	0.991
Bias, m	0.0003	-0.0017

Conclusions and Recommendations

Comparison of CMS-Flow to the analytical solution of flow over a bump verified that the calculated results are accurate for transcritical flows with sharp discontinuities. Both the implicit and explicit flow solvers produced similar results. The adaptive time step of the implicit solver increased the model efficiency and reduced the computational time. However, it is not recommended to use the implicit solution scheme for practical applications in which the physics require small time steps due to sharp discontinuities in the flow and/or extensive wetting and drying because the implicit solver will not be significantly more efficient than an explicit solver.