CR-07-1:Chapter4

Suspended load

Introduction

The earliest transport rate formulas are mainly based on the concept that the sediment transport rate for steady uniform flow can be related to the bottom shear stress (Meyer-Peter and Müller 1948; Einstein 1950; Engelund and Hansen 1972) assuming that bed-load transport prevails. However, if the shear stress is sufficiently large, the particles can be lifted, put in suspension, and transported in large quantities by the current. Thus, suspended load often prevails for fine sediments (d₅₀ < 0.5 mm). The traditional approach for calculating the unsteady depth-averaged volumetric suspended load transport q_ss is to determine the vertical distribution of suspended sediment concentration (c) and velocity (u), after which the product between these two quantities is integrated through the vertical from the edge of the bed-load layer (z = z_a) to the water surface (z = h) (Van Rijn 1993), yielding:

\begin{equation} \tag{111}

 {{q}_{ss}}\left( t \right)=\int_{{{z}_{a}}}^{h}{u\left( z,t \right)c\left( z,t \right)dz}

\end{equation}

where q_ss(t) is the depth-averaged instantaneous suspended load per unit width, u(z,t) and c(z,t) are, respectively, the horizontal velocity and the volume sediment concentration at the height z, z_a is the level at the top of the bed-load layer, and h(t) is the instantaneous water depth. A steady situation is typically assumed to simplify the problem, so time-averaged values $u\left(z\right)={\overline {u\left(z,t\right)}}$ and $c\left(z\right)={\overline {c\left(z,t\right)}}$

are substituted (Figure 39):

\begin{equation} \tag{112} {{q}_{ss}}=\int_{{{z}_{a}}}^{h}{c\left( z \right)u\left( z \right)dz} \end{equation}

Therefore, an accurate estimation of the total suspended load requires accurate prediction of the mean current velocity and concentration profiles.

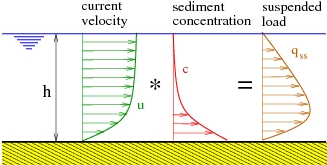
Figure 39. Computation of suspended load over depth.

In the marine coastal environment, the process of sediment transport becomes complex because of the presence of oscillatory flows and the interaction between steady and oscillatory flows. For longshore sediment transport, the effect of the short waves is typically modeled as an additional sediment stirring that increases the bed shear stress and the vertical mixing coefficient for the sediment in suspension (Bijker 1967; Watanabe 1982; Van Rijn 1993).

To describe suspended load above the wave boundary layer, some refined mathematical approaches were proposed during the last decades with sophisticated turbulence closure models (Fredsøe et al. 1985; Davies 1990; Davies et al. 1997). However, the development of practical sediment transport models still has a strong empirical character and relies heavily on physical insight combined with quantitative data obtained through laboratory and field experiments.

An essential part of morphodynamic computations for flow conditions involving suspended sediment transport is the use of a reference concentration as a bed boundary condition. Van Rijn (1984b) proposed that the reference concentration should be a function of the bed-load transport. Furthermore, the main controlling parameters for the suspended load are the settling velocity of the sediment W_s, and more specifically, the vertical sediment diffusion coefficient $\varphi _{v}$. The latter is examined here and compared to the Van Rijn (1984b) results.

In the nearshore, for mild wave conditions, the bed is covered by ripples. These bed forms strongly affect the sediment transport by enhancing the suspended load, but also by modifying the direction of the sediment transport. Assuming $u\left(z,t\right)={\overline {u\left(z,t\right)}}+{\tilde {u}}\left(z,t\right)=u\left(z\right)+{\tilde {u}}\left(z,t\right)$ and $c\left(z,t\right)={\overline {c\left(z,t\right)}}+{\tilde {c}}\left(z,t\right)=c\left(z\right)+{\tilde {c}}\left(z,t\right)$, where ${\tilde {u}}\left(z,t\right)$ and ${\tilde {c}}\left(z,t\right)$ are the oscillatory components, the net suspended sediment transport is obtained by averaging Equation 111:

\begin{equation} \tag{113}

 {{q}_{ss}}=<\int_{{{z}_{a}}}^{h\left( t \right)}{\left[ u\left( z \right)c\left( z \right)+\tilde{u}\left( z,t \right)\tilde{c}\left( z,t \right) \right]}dz>

\end{equation}

\begin{equation} \tag{114} ={{q}_{ss,c}}+{{q}_{ss,w}} \end{equation}

The first term on the right side (Equation 114) corresponds to the current-related suspended load, and the second term corresponds to the wave-related suspended load. The wave-related suspended load includes the quasi-steady suspended load due to asymmetric waves (assuming no phase lag exist between the wave velocity and the sediment concentration) and the unsteady effects due to a possible phase lag between the instantaneous velocity and concentration. Many experimental studies and most predictive models do not take into account the wave-related suspended load, although it appears to be significant for cross-shore sediment transport.

The objective of this study was to develop a reliable and general formulation for the prediction of suspended load transport valid under a wide range of fluvial and coastal conditions. For this purpose, various data sets were used for the model development including steady and oscillatory flows. The study focused on the prediction of the sediment concentration through the water column, establishing relationships for the vertical sediment diffusivity and the reference concentration. Assuming a typical velocity profile, the current-related suspended load can easily be calculated. The second part of this study focused on the possible phase lag affecting the suspended load in the wave direction due to the presence of ripples.