GenCade:Internal Wave Transformation: Difference between revisions
m (Added footer) |
m (Updated equations to latex and footer) |
||
| Line 5: | Line 5: | ||
Wave transformation from the deep water reference depth or the nearshore reference line (depending on whether or not the external wave model is used) is initially conducted without accounting for diffraction from structures located in the model reach. The solution strategy is to obtain a first approximation of breaking wave conditions without including diffraction and then modify the result by accounting for changes to the wave field by each diffraction source. | Wave transformation from the deep water reference depth or the nearshore reference line (depending on whether or not the external wave model is used) is initially conducted without accounting for diffraction from structures located in the model reach. The solution strategy is to obtain a first approximation of breaking wave conditions without including diffraction and then modify the result by accounting for changes to the wave field by each diffraction source. | ||
Omitting diffraction, there are three unknowns in the breaking wave calculation: the wave height, angle, and the depth at breaking. Three equations are needed to obtain these quantities, which are introduced below. These are the equation for the breaking wave height based on reference wave data | Omitting diffraction, there are three unknowns in the breaking wave calculation: the wave height, angle, and the depth at breaking. Three equations are needed to obtain these quantities, which are introduced below. These are the equation for the breaking wave height based on reference wave data, a depth-limited breaking criterion, and a wave refraction equation (Snell’s law). | ||
The height of breaking waves that are transformed by refraction and shoaling are calculated as: | The height of breaking waves that are transformed by refraction and shoaling are calculated as: | ||
<math>H_b = K_RK_SH_{Ref}</math> | |||
where | where <math>H_b</math> is the breaking wave height, <math>K_R</math> is the refraction coefficient, <math>K_S</math> is the shoaling coefficient, and <math>H_{Ref}</math> is the wave height at the offshore reference depth or the nearshore reference line depending on which wave model is used. Both <math>K_R</math> and <math>K_S</math> are calculated in the classical way: | ||
<math>K_R = \sqrt{\frac{cos\theta_1}{cos\theta_2}}</math> and <math>K_S = \sqrt{\frac{C_{g1}}{C_{g2}}}</math> | |||
where | where <math>cos\theta_1</math> is the starting angle of the ray and <math>cos\theta_2</math> is the angle of arrival at <math>P_2</math>, the location of which is determined by the breaking depth, and <math>C_{g1}</math> and <math>C_{g2}</math> are the group velocities at their respective depths (meters/second). | ||
The equation for depth-limited wave breaking is given by: | The equation for depth-limited wave breaking is given by: | ||
<math>H_b = \gamma d_b</math> | |||
where | where <math>\gamma</math> is 0.78. If there are no structures to produce diffraction, the undiffracted wave characteristics are used as input to the sediment transport relation (see [[GenCade:Sand Transport Rates|Sand Transport Rates]]). If such obstacles are present, breaking wave heights and directions are recalculated, as described next. | ||
== Breaking Waves Affected by Structures == | == Breaking Waves Affected by Structures == | ||
| Line 32: | Line 32: | ||
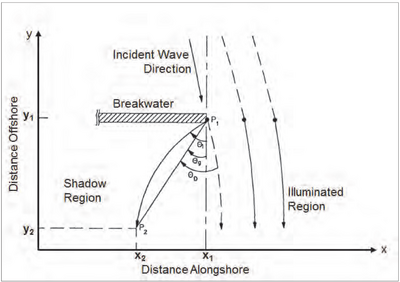
[[File:BreakwaterWaveDiffraction.png|400px|thumb|center|Figure 1. Definition Sketch for the Wave Diffraction Calculation]] | [[File:BreakwaterWaveDiffraction.png|400px|thumb|center|Figure 1. Definition Sketch for the Wave Diffraction Calculation]] | ||
The angle | The angle <math>cos\theta_1</math> at which a wave ray must start to arrive at <math>P_2</math> inside the shadow region is not known prior since it is a function of the breaking criterion as well as the distance alongshore defining the location of grid cells in the numerical calculation. A ray shooting technique can be used to determine <math>cos\theta_1</math> (Kraus 1982, 1984), but this procedure is complex and requires considerable execution time. As a first approximation, the geometric angle θ<sub>g</sub> defined by the straight line between <math>P_1</math> and <math>P_2</math> is used. | ||
Due to the impact of diffraction, the wave height is reduced and, thus, the wave is not breaking. An iterative procedure is used to find the location where the wave, which has been transformed by diffraction, refraction, and shoaling, is breaking. At breaking, the wave fulfills the two conditions: | Due to the impact of diffraction, the wave height is reduced and, thus, the wave is not breaking. An iterative procedure is used to find the location where the wave, which has been transformed by diffraction, refraction, and shoaling, is breaking. At breaking, the wave fulfills the two conditions: | ||
<math>H_b = K_D\theta_DH'_b</math> and <math>H_b = \gamma d_b</math> | |||
Where | Where <math>K_D</math> is a diffraction coefficient, <math>\theta_D</math> is the angle between the incident wave ray at <math>P_1</math> and a straight line between <math>P_1</math> and <math>P_2</math>, if <math>P_2</math> is in the shadow region, <math>H'_b</math> is the breaking wave height at the same cell without diffraction. | ||
For waves that are inside two overlapping shadow zones, an average | For waves that are inside two overlapping shadow zones, an average <math>cos\theta_g</math> is calculated together with a composite <math>K_d</math> coefficient for the two diffracting systems. Then, the same iteration procedure as the one used inside one diffraction system is used. In the illuminated region a similar procedure is used, where a composite <math>K_d</math> is used, but instead of a <math>cos\theta_g</math>, the undiffracted wave direction is used. | ||
Because GenCade was developed to simulate waves and shoreline change in the field, the procedure of Goda et al. (1978) (see also, Goda (1984)) was adapted. Details of application of the method to calculate wave breaking produced by combined diffraction, refraction, and shoaling as used in GenCade are given by Kraus (1981, 1982, 1984, 1988). For given wave conditions at the diffracting tip, the diffraction coefficient is only a function of | Because GenCade was developed to simulate waves and shoreline change in the field, the procedure of Goda et al. (1978) (see also, Goda (1984)) was adapted. Details of application of the method to calculate wave breaking produced by combined diffraction, refraction, and shoaling as used in GenCade are given by Kraus (1981, 1982, 1984, 1988). For given wave conditions at the diffracting tip, the diffraction coefficient is only a function of <math>cos\theta_D</math>. In GenCade, it is assumed that the method is valid for relatively short structures such as detached breakwaters. | ||
== Useful Links == | |||
[[GenCade References| GenCade References]] | |||
[[GenCade| GenCade Home Page]] | [[GenCade| GenCade Home Page]] | ||
[[GenCade#GenCade_Documentation| GenCade Documentation Portal]] | [[GenCade#GenCade_Documentation| GenCade Documentation Portal]] | ||
Revision as of 15:53, 21 December 2022
Note: The Wave Calculation page introduces the internal wave transformation topic within GenCade.
Breaking Waves
Wave transformation from the deep water reference depth or the nearshore reference line (depending on whether or not the external wave model is used) is initially conducted without accounting for diffraction from structures located in the model reach. The solution strategy is to obtain a first approximation of breaking wave conditions without including diffraction and then modify the result by accounting for changes to the wave field by each diffraction source.
Omitting diffraction, there are three unknowns in the breaking wave calculation: the wave height, angle, and the depth at breaking. Three equations are needed to obtain these quantities, which are introduced below. These are the equation for the breaking wave height based on reference wave data, a depth-limited breaking criterion, and a wave refraction equation (Snell’s law).
The height of breaking waves that are transformed by refraction and shoaling are calculated as:
where is the breaking wave height, is the refraction coefficient, is the shoaling coefficient, and is the wave height at the offshore reference depth or the nearshore reference line depending on which wave model is used. Both and are calculated in the classical way:
and
where is the starting angle of the ray and is the angle of arrival at , the location of which is determined by the breaking depth, and and are the group velocities at their respective depths (meters/second).
The equation for depth-limited wave breaking is given by:
where is 0.78. If there are no structures to produce diffraction, the undiffracted wave characteristics are used as input to the sediment transport relation (see Sand Transport Rates). If such obstacles are present, breaking wave heights and directions are recalculated, as described next.
Breaking Waves Affected by Structures
Structures such as detached breakwaters, jetties, and groins which extend well seaward of the surf zone intercept the incident waves prior to breaking. Headlands and islands (specified as structures in GenCade) may also intercept waves. In the following discussion, all such objects are referred to as structures. Each tip of a structure will produce a near- circular wave pattern, and this distortion of the wave field is a significant factor controlling the response of the shoreline in the lee of the structure. Sand typically accumulates in the diffraction shadow of a structure, being transported from one or both sides by the oblique wave angles in the circular wave pattern and the decrease in wave height alongshore with penetration into the shadow region. Accurate and efficient calculation of waves transforming under combined diffraction, refraction, and shoaling to break is required to obtain realistic predictions of shoreline change in such situations.
Figure 1 is a definition sketch of the calculation procedure for the breaking wave height and angle behind a structure (Kraus 1981, 1982, 1984). Conceptually, the area of interest is separated into a shadow region and an illuminated region by a wave ray directed toward the beach from the tip of the structure at the same angle as the incident waves arriving at the tip. To determine the breaking wave height, a diffraction coefficient must be calculated in both regions because the diffraction effect can extend far into the illuminated region. To determine the breaking wave angle inside the shadow region, wave rays are assumed to proceed radially from the tip of the structure P1 at an angle θ1 to arrive at some point P2 with an angle θ2, where they break.
The angle at which a wave ray must start to arrive at inside the shadow region is not known prior since it is a function of the breaking criterion as well as the distance alongshore defining the location of grid cells in the numerical calculation. A ray shooting technique can be used to determine (Kraus 1982, 1984), but this procedure is complex and requires considerable execution time. As a first approximation, the geometric angle θg defined by the straight line between and is used.
Due to the impact of diffraction, the wave height is reduced and, thus, the wave is not breaking. An iterative procedure is used to find the location where the wave, which has been transformed by diffraction, refraction, and shoaling, is breaking. At breaking, the wave fulfills the two conditions:
and
Where is a diffraction coefficient, is the angle between the incident wave ray at and a straight line between and , if is in the shadow region, is the breaking wave height at the same cell without diffraction.
For waves that are inside two overlapping shadow zones, an average is calculated together with a composite coefficient for the two diffracting systems. Then, the same iteration procedure as the one used inside one diffraction system is used. In the illuminated region a similar procedure is used, where a composite is used, but instead of a , the undiffracted wave direction is used.
Because GenCade was developed to simulate waves and shoreline change in the field, the procedure of Goda et al. (1978) (see also, Goda (1984)) was adapted. Details of application of the method to calculate wave breaking produced by combined diffraction, refraction, and shoaling as used in GenCade are given by Kraus (1981, 1982, 1984, 1988). For given wave conditions at the diffracting tip, the diffraction coefficient is only a function of . In GenCade, it is assumed that the method is valid for relatively short structures such as detached breakwaters.