CR-07-1:Chapter1: Difference between revisions
No edit summary |
mNo edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 72: | Line 72: | ||
---- | ---- | ||
{|cellspacing="0" cellpadding = "10" | {|cellspacing="0" cellpadding = "10" | ||
|[[ | |[[CR-07-1|Table of Contents]] | ||
| style="width:60%" | | | style="width:60%" | | ||
| style="align-text:right"|[[ | | style="align-text:right"|[[CR-07-1:Chapter2|Chapter 2 - General Sediment Transport Properties]] | ||
|} | |} | ||
[[category: | [[category:Publication]] | ||
Latest revision as of 20:15, 21 March 2012
Introduction
Background
Many sediment transport formulas have been developed through the years for application in coastal areas (for example, see Bayram et al. 2001; Camenen and Larroudé 2003). However, these formulas have typically described a specific set of physical processes, which limits their applicability in a situation where many processes act simultaneously to transport the sediment as, for example, around a coastal inlet. Also, most formulas have been validated with limited data. Thus, there is a lack of general and consistent sediment transport formulas valid under a wide range of hydrodynamic, sedimentologic, and morphologic conditions that yield reliable and robust predictions. In this report, such a formulation is presented and validated against a large set of laboratory and field data on longshore and cross-shore sediment transport.
The coastal environment at an inlet encompasses hydrodynamic forcing of many types, where waves, tides, wind, and river runoff are the most important agents for initiating water flow and associated sediment transport. Besides the oscillatory motion, waves induce mean currents in the surf zone (longshore currents, rip currents, etc.), stir and maintain sediment in suspension through the breaking process, and cause swash motion and transport on the foreshore. The wind and tide generate mean circulation patterns that move sediment, especially in combination with waves. Also, on the bay side and in the vicinity of the inlet throat, river discharge to the bay might generate currents that significantly contribute to the net transport. Figure 1 schematically illustrates some of the hydrodynamic forcing around an inlet that contributes to the mobilization and transport of sediment.
Predicting sediment transport and morphologic evolution around a coastal inlet is necessary in support of engineering activities that ensure proper functioning of the inlet for navigation (Figure 2). Optimizing dredging operations in response to channel shoaling or minimizing local scour, which may threaten jetty integrity, are examples of such activities. Furthermore, natural bypassing of sediment through the inlet shoals and bars is required to supply material to downdrift beaches, and a reduction in this transport may cause erosion and shoreline recession. After an inlet opens, as the shoals and bars grow with little bypassing transport, downdrift erosion is common, and varying engineering measures such as beach nourishment and structures might be needed. On the updrift side of an inlet, accumulation normally occurs, especially if the inlet has been stabilized with jetties, with shoreline advance and increased infilling of the channel.

Figure 1. Hydrodynamic processes controlling sediment transport in an inlet environment (slide courtesy of N. C. Kraus).

Figure 2. Natural processes around an inlet for which predictions of sediment transport and morphological evolution are of importance (slide courtesy of N. C. Kraus).
For these kinds of engineering-support studies, a gap has existed between semi-empirical approaches yielding estimates of transport rates for small scales (e.g., for a fixed water depth and with a temporal average over several wave periods) and the more empirical approach giving an assessment of mean sediment rate at larger scales (e.g., mean value for the surf zone based on formulas calibrated against long-term data). Here, the main objective is to develop reliable formulas that can predict net transport rates yielding the daily evolution (including storms), as well as the monthly and yearly evolution (seasonal and long-term forcing) in support of predictive numerical models of morphology change and channel evolution at coastal inlets for engineering design and planning. The main imposed hydrodynamic forcing for the sediment transport is the mean current (e.g., wave-induced longshore current and tidal current). If the cross-shore evolution of the beach is neglected, the influence of waves can be simplified as a stirring effect (Figure 3). Emphasis is given to suspended sediment and the action of breaking waves on the suspension. Moreover, to solve problems of channel infilling, the contribution of gravity should be included. With the objective of simulating long-term evolution, simplifications are introduced for many of the governing phenomena to limit computation time and reduce input requirements.
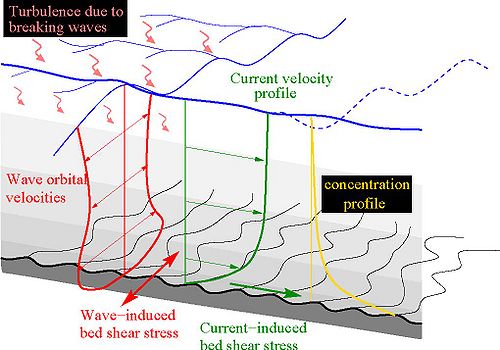
Figure 3. Hydrodynamic forcing determining conditions for longshore sediment transport (after Soulsby 1997).
Elements of the sediment transport formulation undertaken in the present study can be summarized as follows:
1. Develop sediment transport rate formulas valid at several different scales (a variety of formulas is needed).
2. Target both a general detailed model (modeling system) and predictive models for more specific purposes.
3. Build on previous work (existing formulas) for a wide variety of conditions, but identify limitations and extend applicability by enhancements.
4. Validate with both "point" and "area" data (from laboratory and field).
5. Test models for a variety of conditions to ensure robustness, reliability, and efficiency.
6. Introduce morphologic constraints, as required.
For this kind of study, the transport modeling system employed is classical in requiring or including typically available or calculated information. Figure 4 shows the principal components of such a system. An example is the Coastal Modeling System developed in the Coastal Inlets Research Program (Buttolph et al. 2006).
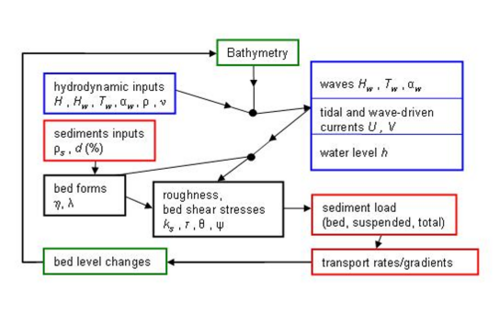
Figure 4. Sediment transport formulation.
Objectives
There is a great need for predictive sediment transport rate formulas that take into account a wide range of physical factors and conditions encountered near coastal inlets and their navigation channels. Such formulas should be compared with measurements from the laboratory and field including many different situations to ensure robust and reliable behavior. A general sediment transport formula should yield predictions of the transport rate for the following conditions:
1. Bed load and suspended load.
2. Waves and currents.
3. Breaking and nonbreaking waves.
4. Bed slope.
5. Initiation of motion.
6. Asymmetric wave velocity.
7. Arbitrary angle between waves and current.
In this report, general formulas to compute the sediment transport rate developed that are valid under these conditions. Other phenomena or mechanisms may also be of importance, such as the phase lag between water and sediment motion or the influence of bed forms. Modifications to the general formula are derived to take these phenomena into account. The theoretical descriptions of the various mechanisms appearing for the conditions listed here are of differing sophistication, and not all of them can easily be validated with data at this time. Thus, another crucial feature of a general sediment transport formulation is that the different components can be replaced as improved descriptions become available.
The purpose of the present report is to develop a general sediment transport formulation to be applied in an inlet environment where both waves and currents control the transport rate. Emphasis on the development is to arrive at a formulation that is robust and yields reliable predictions over a wide range of input conditions. Also, all relevant physical processes should be included to obtain a formula of greatest generality. Initial development may include simpler formulations for some of these processes, but as physical understanding improves, such components may be replaced by more comprehensive approaches. Because the primary objective was to develop a robust and reliable formulation applicable under many different conditions, a large database on sediment transport measurements in the laboratory and field was assembled to test different aspects of the formulas to assure that they join smoothly through various combinations of forcing conditions.
Procedure
The strategy in the development was to derive straightforward predictive formulas to describe various governing physical processes of sediment transport and then validate these with data. At the initial stage, comparisons were made between existing formulas and data to see how well they performed and if these formulas could serve as a starting point for development of more general formulas. First, bed load under a steady current was investigated, and an extensive database was compiled for comparison with existing formulas. To improve the predictive capability, a slightly modified version of these transport formulas was developed that includes a different description of the criterion for incipient motion. A factor was added in the bed-load formula to describe the effect of bottom slope on the transport rate. The formula was then generalized to encompass waves at an arbitrary angle to the current, including the case of waves with an asymmetric velocity variation over a period (i.e., non-sinusoidal waves). A database on sediment transport under waves with and without a mean current was compiled, and the derived formula was compared with these data.
After studying conditions where bed-load transport was dominant, the formulation was extended to describe suspended load transport. The suspended transport rate was derived from the product of a concentration and mean velocity integrated over the water depth. An exponential function was employed to characterize the reduction in sediment concentration with distance from the bed, and a uniform velocity through the water column was assumed. Calculated sediment concentration distributions were compared with measurements, both for the case of waves and for currents. The vertical mixing coefficient, which determines the decay in concentration with distance from the bed, was expressed as a function of the energy dissipation. This dissipation includes contributions of currents and waves, where both bottom friction and breaking were taken into account for the waves. The reference concentration at the bottom was expressed in terms of the bed-load transport.
| Table of Contents | Chapter 2 - General Sediment Transport Properties |