Circ Basin: Difference between revisions

From CIRPwiki
Jump to navigation Jump to search
(Created page with "{{Equation|1=<math>\eta = \left{\matrix{ {\frac{W x_1 x_2}{2ghR}}{f_c=0} } {{\frac{W f_c}{Rgh\kappa} \left[ \frac{R^2}{8} + \...")
 
No edit summary
 
(4 intermediate revisions by the same user not shown)
Line 1: Line 1:
{{Equation|1=<math>\eta = \left{\matrix{
'''Test C1-Ex2: Wind-driven Flow in a Circular Basin'''
     {\frac{W x_1 x_2}{2ghR}}{f_c=0} }
 
          {{\frac{W f_c}{Rgh\kappa}
''Purpose''
          \left[
 
The purpose of this test is to verify the steady state linear
hydrodynamics when forced by spatially variable winds, a linear bottom
friction, and with and without Coriolis force. Specific model features
evaluated in this problem are spatially variable winds and Coriolis
force.
 
''Problem''
 
Assuming steady state conditions and no advection, diffusion, waves or
spatial gradients in atmospheric pressure, the governing equations
reduce to
 
{{Equation|1=<math>\frac{\partial \left(hU_j\right)}{\partial x_j} = 0 </math> | 2=1}}
 
{{Equation|1=<math>\epsilon_{ij}f_chU_j = -gh \frac{\partial \eta}{\partial x_i} + \frac{1}{\rho}\left(\tau^s_i-\tau^b_i\right)</math> | 2=2}}
 
 
where <math>\epsilon_{ij}</math> is the permutation operator equal to
1 for <math>i,j=1,2</math>; -1 for <math>i,j=2,1</math>; and 0 for
<math>i=j</math>, <math>f_c</math> is the Coriolis parameter,
<math>U_j</math> is the depth-averaged current velocity in the
<math>j</math>th direction, <math>\tau^s_i</math> is the wind driving
force per unit water surface area, and <math>\tau^b_i</math> is the
bottom friction. The problem is further simplified by assuming a flat
bed and deep water conditions <math>h>>\eta</math> , so that
<math>h</math> may be considered constant. A linear bottom friction is
specified as <math>\tau^b_i=\epsilon_{i2}x_jW/R </math> where
<math>f_c</math> is a linear bottom friction coefficient. The wind
stress is given by where <math>W</math> is the gradient or slope of
the wind speed and <math>R</math> is the radius of the circular basin.
 
''Analytical Solution''
 
Dupont (2001) presented the analytical solution to the problem
above. The water surface elevation is given by
 
{{Equation|1=
<math>\eta =
\begin{array}{cc}
     \frac{W x_1 x_2}{2ghR} &  f_c=0  \\
    \frac{W f_c}{Rgh\kappa} \left[
             \frac{R^2}{8}
             \frac{R^2}{8}
             + \frac{1}{4}\left(\frac{2\kappa x_1 x_2}{f_c}-x_1^2-x_2^2\right)
             + \frac{1}{4}\left(\frac{2\kappa x_1 x_2}{f_c}-x_1^2-x_2^2\right)
         \right]}{f_c \neq 0}}
         \right]       &  f_c \neq 0
        }
\end{array}
        \right. | </math> | 2=3}}
     
</math> | 2=3}}
 
The current velocities are independent of the Coriolis coefficient and
are given by
 
{{Equation|1=
<math>
U_i = \frac{\epsilon_{ij}x_jW}{2Rh\kappa}
</math> | 2=4}}
 
 
''Model Setup''
 
The computational grid, shown in Figure 4, has 5 levels of refinement
from 2km to 125m and a total of 15,272 computational cells.
 
[[File:wind_circular_basin.png ||leftthumb|400px|alt=framework]]
Figure 4. CMS-Flow computational grid used for the wind-driven flow in
a circular basin.
 
The CMS model is run to steady state from zero current and water level
as initial conditions. The relevant model parameters are summarized in
Table 4. Two cases are run: one with Coriolis and one without.
 
 
{| class="wikitable" border="1"
|+ Table 4. CMS-Flow setup for the circular basin test case.
! Parameter  !! Value
|-
| Time step ||  1 hr
|-
| Simulation duration  ||  72 hr
|-
| Ramp period duration ||  24 hr
|-
| Water depth  ||  100 m
|-
| Mixing terms  ||  Off
|-
| Wall friction ||  Off
|-
| Linear bottom friction || On
|-
|coefficient      ||  0.001
|-
|Coriolis    ||  0.0, 0.0001 rad/s
|-
|Wind gradient    ||  0.0001<math>m^2/s^2</math>
|}
 
 
''Results and Discussion''
 
''Without Coriolis Force''
 
A comparison of the calculated and analytical current velocities and
water levels in the case without Coriolis force are shown in
Figure 5. The goodness-of-fit statistics for the velocity components
and water level are shown in Table 5. The calculated water level shows
excellent agreement with the analytical solution, even along the outer
boundary, and is demonstrated by the NMAE of 0.02%. The current
velocities agree well with the analytical solution. The largest errors
for the current velocities occur near the outer boundary due to the
staircase representation of the curved boundary. The error is reduced
by increasing the refinement at the boundary.
 
[[File:analytical_without_coriolis.png||leftthumb|400px|alt=framework]]
[[File:calculated_without_coriolis.png||leftthumb|400px|alt=framework]]
Figure 5. Analytical (a) and calculated (b) current velocities
and water levels without Coriolis force.
 
 
 
 
{| class="wikitable" border="1"
|+ Table 5. Water level and current velocity goodness-of-fit statistics*
for the circular basin test case without Coriolis force
! Variable  !!    NRMSE, % !!  NMAE, % !! <math>R^2</math> !! Bias
|-
|U-velocity  ||    1.88      ||  0.30    || 0.999          || -4.5e-7 m/s
|-
|V-velocity  ||    2.51      ||  0.37    || 0.998          || 9.7e-9 m/s
|-
|Water level ||    0.03      ||  0.02    || 0.999          || 3.14e-8 m
|-
*defined in Appendix A
|}
 
 
''With Coriolis Force''
 
A comparison of the calculated and analytical solutions of current
velocities and water levels for the case with Coriolis force is shown
in Figure 6. The goodness-of-fit statistics for the velocity
components and water level are shown in Table 6. Similar to the case
without Coriolis force, agreement between the calculated water
elevation and current velocity and the analytical solutions resulted
in a NRMSE of 0.03% for water level and 2.53% for current
velocities. The largest errors in current velocity occur adjacent to
the outer boundary where the curved boundary exists. A positive
Coriolis parameter corresponds to the northern hemisphere where ocean
currents are deflected to the right. For this case, the Coriolis force
has the net effect of pushing water towards the center of the circular
basin creating higher water levels and lower water levels around the
perimeter.
 
From Equation (4), it can be seen that the water level, <math>\eta</math>, at
the basin center <math>x_1=x_2=0m</math>, is equal to
<math>Wf_cR/\left(8gh\kappa\right) </math>
for <math>f_c \neq 0/s</math> and equal to 0m for 0/s.
 
[[File:analytical_with_coriolis.png ||  leftthumb|400px|alt=framework]]
[[File:calculated_with_coriolis.png ||  leftthumb|400px|alt=framework]]
Figure 6. Analytical (a) and calculated (b) current velocities
and water levels with Coriolis force.
 
{| class="wikitable" border="1"
|+ Table 6. Water level and current velocity goodness-of-fit statistics*
for the circular basin test case with Coriolis
!Variable    !! NRMSE, %      !! NMAE, %    !! R2    !! Bias
|-
|U-Velocity    || 1.90        || 0.30      || 0.999||-4.5e-7 m/s
|-
|V-Velocity    || 2.51        || 0.37        || 0.998||4.6e-9 m/s
|-
|Water level    || 0.03        || 0.02        || 0.999||9.5e-8 m
|-
*defined in Appendix A
|}
 
 
''Conclusions and Recommendations ''
 
The analytical solution for the steady-state wind-induced linear
hydrodynamics in a closed circular basin was simulated. Computed water
levels were accurate within 0.03% NRMSE, and showed little influence
from the staircase representation of the curved outer
boundary. Current velocities were less accurate with a NRMSE of 2.53%
due to errors near the outer boundary.  For most coastal applications
open boundaries are represented by straight boundaries so the
staircase boundary does not exist. Curved boundaries usually occur
along the wet-dry interface in very shallow water where the current
velocities are usually small due to the increased bottom
friction. However, if the curved boundary occurs in deep water or in
areas where the current velocities are strong, then errors will be
incurred due to the staircase representation of the
boundary. Nevertheless, the errors may be reduced by increasing the
grid refinement along the specific boundary. In the future, this
problem can be eliminated by implementing a boundary fitting method,
such as a cut-cell or embedded boundary, or quadrilateral mesh.

Latest revision as of 21:58, 15 April 2014

Test C1-Ex2: Wind-driven Flow in a Circular Basin

Purpose

The purpose of this test is to verify the steady state linear hydrodynamics when forced by spatially variable winds, a linear bottom friction, and with and without Coriolis force. Specific model features evaluated in this problem are spatially variable winds and Coriolis force.

Problem

Assuming steady state conditions and no advection, diffusion, waves or spatial gradients in atmospheric pressure, the governing equations reduce to

  Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{\partial \left(hU_j\right)}{\partial x_j} = 0 } (1)
  Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon_{ij}f_chU_j = -gh \frac{\partial \eta}{\partial x_i} + \frac{1}{\rho}\left(\tau^s_i-\tau^b_i\right)} (2)


where Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon_{ij}} is the permutation operator equal to 1 for Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i,j=1,2} ; -1 for Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i,j=2,1} ; and 0 for Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i=j} , Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f_c} is the Coriolis parameter, Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle U_j} is the depth-averaged current velocity in the Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle j} th direction, Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \tau^s_i} is the wind driving force per unit water surface area, and Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \tau^b_i} is the bottom friction. The problem is further simplified by assuming a flat bed and deep water conditions Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h>>\eta} , so that Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h} may be considered constant. A linear bottom friction is specified as Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \tau^b_i=\epsilon_{i2}x_jW/R } where Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f_c} is a linear bottom friction coefficient. The wind stress is given by where Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle W} is the gradient or slope of the wind speed and Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle R} is the radius of the circular basin.

Analytical Solution

Dupont (2001) presented the analytical solution to the problem above. The water surface elevation is given by

  Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \eta = \begin{array}{cc} \frac{W x_1 x_2}{2ghR} & f_c=0 \\ \frac{W f_c}{Rgh\kappa} \left[ \frac{R^2}{8} + \frac{1}{4}\left(\frac{2\kappa x_1 x_2}{f_c}-x_1^2-x_2^2\right) \right] & f_c \neq 0 \end{array} } (3)

The current velocities are independent of the Coriolis coefficient and are given by

  Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle U_i = \frac{\epsilon_{ij}x_jW}{2Rh\kappa} } (4)


Model Setup

The computational grid, shown in Figure 4, has 5 levels of refinement 

from 2km to 125m and a total of 15,272 computational cells.

framework Figure 4. CMS-Flow computational grid used for the wind-driven flow in a circular basin.

The CMS model is run to steady state from zero current and water level as initial conditions. The relevant model parameters are summarized in Table 4. Two cases are run: one with Coriolis and one without.


Table 4. CMS-Flow setup for the circular basin test case.
Parameter Value
Time step 1 hr
Simulation duration 72 hr
Ramp period duration 24 hr
Water depth 100 m
Mixing terms Off
Wall friction Off
Linear bottom friction On
coefficient 0.001
Coriolis 0.0, 0.0001 rad/s
Wind gradient 0.0001Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle m^2/s^2}


Results and Discussion

Without Coriolis Force

A comparison of the calculated and analytical current velocities and water levels in the case without Coriolis force are shown in Figure 5. The goodness-of-fit statistics for the velocity components and water level are shown in Table 5. The calculated water level shows excellent agreement with the analytical solution, even along the outer boundary, and is demonstrated by the NMAE of 0.02%. The current velocities agree well with the analytical solution. The largest errors for the current velocities occur near the outer boundary due to the staircase representation of the curved boundary. The error is reduced by increasing the refinement at the boundary.

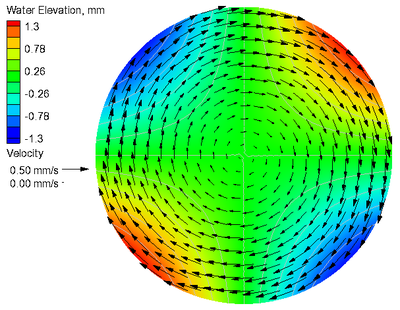
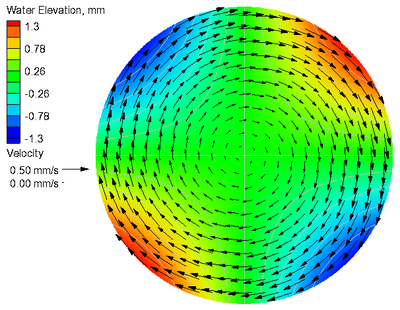framework framework Figure 5. Analytical (a) and calculated (b) current velocities and water levels without Coriolis force.



  • defined in Appendix A
Table 5. Water level and current velocity goodness-of-fit statistics* for the circular basin test case without Coriolis force
Variable NRMSE, % NMAE, % Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle R^2} Bias
U-velocity 1.88 0.30 0.999 -4.5e-7 m/s
V-velocity 2.51 0.37 0.998 9.7e-9 m/s
Water level 0.03 0.02 0.999 3.14e-8 m


With Coriolis Force

A comparison of the calculated and analytical solutions of current velocities and water levels for the case with Coriolis force is shown in Figure 6. The goodness-of-fit statistics for the velocity components and water level are shown in Table 6. Similar to the case without Coriolis force, agreement between the calculated water elevation and current velocity and the analytical solutions resulted in a NRMSE of 0.03% for water level and 2.53% for current velocities. The largest errors in current velocity occur adjacent to the outer boundary where the curved boundary exists. A positive Coriolis parameter corresponds to the northern hemisphere where ocean currents are deflected to the right. For this case, the Coriolis force has the net effect of pushing water towards the center of the circular basin creating higher water levels and lower water levels around the perimeter.

From Equation (4), it can be seen that the water level, Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \eta} , at the basin center Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_1=x_2=0m} , is equal to Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Wf_cR/\left(8gh\kappa\right) } for Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f_c \neq 0/s} and equal to 0m for 0/s.

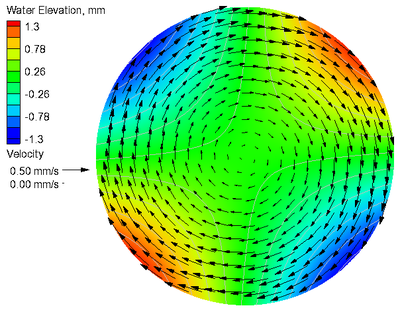
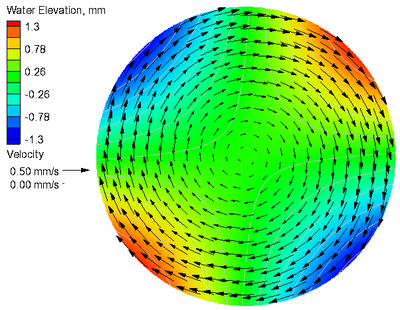framework framework Figure 6. Analytical (a) and calculated (b) current velocities and water levels with Coriolis force.

  • defined in Appendix A
Table 6. Water level and current velocity goodness-of-fit statistics* for the circular basin test case with Coriolis
Variable NRMSE, % NMAE, % R2 Bias
U-Velocity 1.90 0.30 0.999 -4.5e-7 m/s
V-Velocity 2.51 0.37 0.998 4.6e-9 m/s
Water level 0.03 0.02 0.999 9.5e-8 m


Conclusions and Recommendations

The analytical solution for the steady-state wind-induced linear hydrodynamics in a closed circular basin was simulated. Computed water levels were accurate within 0.03% NRMSE, and showed little influence from the staircase representation of the curved outer boundary. Current velocities were less accurate with a NRMSE of 2.53% due to errors near the outer boundary. For most coastal applications open boundaries are represented by straight boundaries so the staircase boundary does not exist. Curved boundaries usually occur along the wet-dry interface in very shallow water where the current velocities are usually small due to the increased bottom friction. However, if the curved boundary occurs in deep water or in areas where the current velocities are strong, then errors will be incurred due to the staircase representation of the boundary. Nevertheless, the errors may be reduced by increasing the grid refinement along the specific boundary. In the future, this problem can be eliminated by implementing a boundary fitting method, such as a cut-cell or embedded boundary, or quadrilateral mesh.

Retrieved from "https://cirpwiki.info/index.php?title=Circ_Basin&oldid=10495"