GenCade:Basic Governing Equations: Difference between revisions
Addition of Figure |
mNo edit summary |
||
| Line 8: | Line 8: | ||
'''ΔV = ΔxΔy(D<sub>B</sub>+D<sub>C</sub>) = (ΔQ/Δx)ΔxΔt +qΔxΔt''' | '''ΔV = ΔxΔy(D<sub>B</sub>+D<sub>C</sub>) = (ΔQ/Δx)ΔxΔt +qΔxΔt''' | ||
[[File:Shoreline_Change_Calculation.png|500px|thumb|center|The definition sketch showing a cross sectional view and a plan view of a dx dy segment of the shoreline with boundary conditions.]] | [[File:Shoreline_Change_Calculation.png|500px|thumb|center|The definition sketch showing a cross sectional view and a plan view of a dx dy segment of the shoreline with boundary conditions.]] | ||
Revision as of 15:21, 20 December 2022
The governing equation of GenCade is primarily formed by conversion of sand volume. The assumption that the beach profile translates seaward or shoreward along a section of coast without changing shape. During an interval of time (Δt), a net amount of sand enters or leaves the section. The change in shoreline position is Δy, the length of the shoreline segment is Δx, and the profile moves within a vertical extent defined by the berm elevation DB and the closure depth DC, both measured from the vertical datum (for example, MSL or MLLW).
The resulting change in volume along the four sides of the area is therefore calculated as:
ΔV = ΔxΔy(DB+DC)
A definition sketch is shown in the figure below. If there is a difference between the net amount longshore sediment transport (Q, in m3/second), the volume changes. The contribution from a line source or sink is included as the term q, where q is the sum of the addition or removal of sand per unit width of beach from either the shoreward or offshore sides. Thus:
ΔV = ΔxΔy(DB+DC) = (ΔQ/Δx)ΔxΔt +qΔxΔt
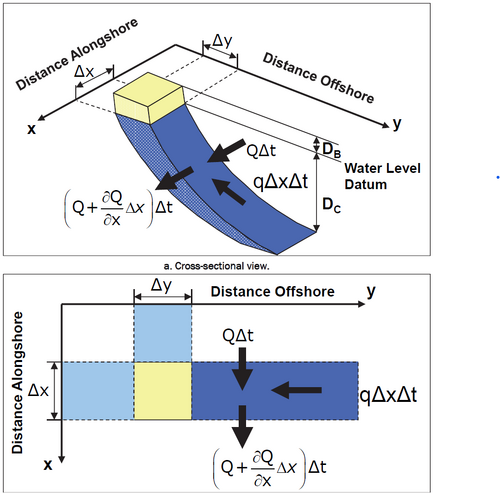
As Δt goes to zero, a differential equation is produced that is the governing equation for the rate of change of the shoreline position:
δy/δt + (1/(DB+DC)) * (δQ/δx - q) = 0
This equation is solved with the inputs of boundary conditions and values for Q, q, DB and DC given.