GenCade Basic Governing Equations
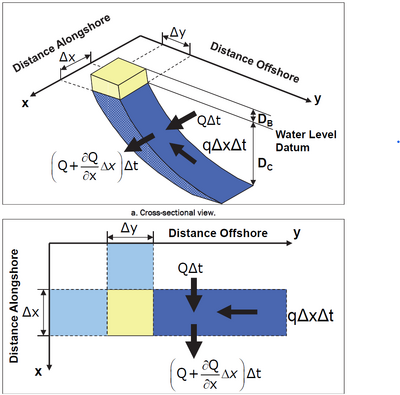
The governing equation of GenCade is primarily formed by conservation of sand volume. The assumption is that the beach profile translates seaward or shoreward along a section of coast without changing shape. During an interval of time (Δt), a net amount of sand enters or leaves the section. The change in shoreline position is Δy, the length of the shoreline segment is Δx, and the profile moves within a vertical extent defined by the berm elevation DB and the closure depth DC, both measured from the vertical datum (for example, MSL or MLLW).
The resulting change in volume along the four sides of the area is therefore calculated as:
A definition sketch is shown in Figure 1.
If there is a difference between the updrift and downdrift longshore sediment transport (Q, in cubic meters/second), then the volume either expands or contracts shifting the shoreline seaward or shoreward, respectively. The contribution from a line source or sink is included as the term q, where q is the sum of the addition or removal of sand per unit width of beach from either the shoreward or offshore sides. Thus:
As Δt goes to zero, a differential equation is produced that is the governing equation for the rate of change of the shoreline position:
This equation is solved with the inputs of boundary conditions and values for Q, q, DB and DC given.