GenCade Val:Benchmark Cases

Figure 29. GenCade straight shoreline with no structures domain.

Figure 30. GenCade straight shoreline with single groin domain.

Figure 29. GenCade straight shoreline with no structures domain.

Figure 30. GenCade straight shoreline with single groin domain.

A series of standardized test cases was developed to demonstrate isolated GenCade model capabilities and verify results against established legacy models (e.g., GENESIS). Simple idealized cases focusing on each of the primary model processes and coastal structures were evaluated separately.Isolation of individual modeled components is an effective means of examining the fundamental skill of a model and can be a practical tool for identifying potential errors, oversights, or omissions when investigating individual components of the model under simple idealized cases.A series of standardized test cases was developed to demonstrate isolated GenCade model capabilities and verify results against established legacy models (e.g., GENESIS). Simple idealized cases focusing on each of the primary model processes and coastal structures were evaluated separately. Isolation of individual modeled components is an effective means of examining the fundamental skill of a model and can be a practical tool for identifying potential errors, oversights, or omissions when investigating individual components of the model under simple idealized cases.

The standardized benchmark cases developed here are separated into the primary coastal structures and project components that are frequently applied in GenCade. Each of the cases is presented with a range in wave forcing to test symmetry of process calculation. GENESIS simulations were also developed following corresponding test cases to evaluate how GenCade results agree with the well-validated legacy model and to support user-confidence for the transfer and migration from GENESIS.

GenCade model setup

Model domain

Figure 31. GenCade straight shoreline with detached breakwater domain.

Figure 32. GenCade straight shoreline with T-head groin domain.

Figure 33. GenCade straight shoreline with seawall domain.

Figure 34. GenCade straight shoreline with beachfill domain.

Figure 35. GenCade straight shoreline with structured inlet domain.

Two categories of idealized model domains were developed for the standardized benchmark cases: straight shoreline domains and concave embayment domains. The purpose of the straight shoreline domains is to provide an uncomplicated foundation to test the most fundamental processes and the impact of coastal structures within the GenCade model. The purpose of the concave embayment domains is to examine the effects wave forcing and structures have on a continuous and uniform alongshore shoreline angle gradient and examine regional contour capabilities. Figures 29 through 35 show each of the seven domains in the straight shoreline category. Figure 29 represents the simplest case with a straight shoreline and no structures or project features within the domain. Figures 30 through 35 build upon this domain with the addition of individual coastal structures or project components. These structures or components include: a single groin (Figure 30), a detached breakwater (Figure 31), a T-head groin (Figure 32), a seawall with a groin to force shoreline erosion to the seawall (Figure 33), a beach fill project (Figure 34), and an inlet with jetties (Figure 35).

Figures 36 and 37 show the two domains in the concave shoreline category. The concave shorelines were developed using a simple quadratic formula to maintain symmetry. The quadratic function employed for these concave shorelines was:

y = ax2

where a = 10^-4. Figure 36 represents a simple case with a concave shoreline and no structures or project features within the domain. Figure 37 builds upon this domain with the addition of two groins.

Figure 36. GenCade concave shoreline with no structures.

Figure 37. GenCade concave shoreline with two groins.

Model forcing: waves

Simulations of the standardized benchmark cases were conducted under various wave forcing. Constant wave forcing over the entire length of the simulation was initially examined for general investigation purposes. First constant waves with 0.75 m offshore wave height and 8 sec period were applied as forcing for both positive wave angles at +15-deg and negative wave angles at -15-deg. Wave forcing simulations were also conducted for constant zero-deg (i.e., shore normal) angles and simulations for all angles between +85-deg and -85-deg in 5-deg increments, but since the net shoreline change for these simulations results in zero change, they are not presented here. For all cases, wave inputs were supplied at the 50 m depth contour.

Model parameters

Wherever possible, the model parameters were held constant between each of the simulations in each domain category for purposes of consistency of comparison between simulations. Table 1 presents the model parameters common to all the standardized benchmark cases in the straight shoreline domains.

Table 1. Model parameters common to all benchmark cases.

Parameter	Value
DX, m	10
NX	300 (Straight Domain); 360 (concave Domain)
DT, hr	0.5
K1	0.5
K2	0.25
ISMOOTH, # Cells in Smoothing Window	3
Non-Jetty boundary condition	Pinned

GenCade model results and discussion

No structures

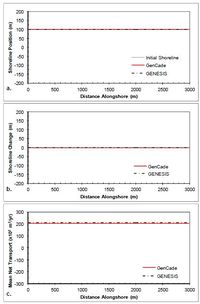
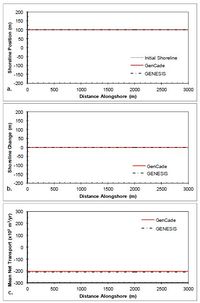
The simplest case of a straight shoreline without any coastal structures or coastal project components is presented first. Figure 38 shows the results after a 2-year simulation with constant +15-deg wave angle forcing. As one would expect, there is zero shoreline change since the alongshore gradients in transport are zero and transport is constant at approximately 200,000 m3/yr. Figure 39 shows the results after a 2-year simulation with constant -15-deg wave angle forcing. Similar to the positive wave angle forcing case, there is zero shoreline change since the alongshore gradients in transport are zero. Figure 39(c) indicates that transport is constant at approximately -200,000 m3/yr. Results for all simulations with no structures result in good agreement between GenCade results and GENESIS results.

• Figures 38-39
• 

  Figure 38. Calculated (a) shoreline position, (b) shoreline change, and (c) mean net transport for straight shoreline with no structures; H0 = 0.75 m, T = 8 sec, θ0 = +15-deg.

• 

  Figure 39. Calculated (a) shoreline position, (b) shoreline change, and (c) mean net transport for straight shoreline with no structures; H0 = 0.75 m, T = 8 sec, θ0 = -15-deg.

Single groin

A case having a straight shoreline with a single groin 75 m long (175 m from the grid origin) at the center of the domain is presented next to examine shoreline response to the presence of a groin. Figure 40 shows the results after a 2-year simulation with constant +15-deg wave angle forcing. The groin presents an obstruction to longshore transport, which results in a reduction of transport rates as sediment is bypassed around the groin. This local transport reduction in the vicinity of the groin translates to a gradient in transport rates as transport transitions to and from background rates. This difference in sediment transport potential accounts for the accretion of sediment and resulting shoreline progradation seaward on the left (updrift) side of the groin as the transport rates decrease from 200,000 m3/yr to approximately 50,000 m3/yr at the groin. Conversely, as transport rates increase from 50,000 m3/yr in the vicinity of the groin back to 200,000 m3/yr outside of the region of groin influence, the expected downdrift shoreline erosion is observed. Figure 41 presents the results after a 2-year simulation with constant -15- deg wave angle forcing. The opposite pattern is observed in this example because transport is forced by negative wave angles relative to shore normal. Figure 41(c) shows that an increase in transport occurs on the left(downdrift) side of the groin from -200,000 m3/yr background transport rate to -50,000 m3/yr in the vicinity of the groin. This positive gradient results in erosion while the negative gradient on the right (updrift) side of the groin results in accretion. Figures 40 and 41 clearly depict excellent agreement between GenCade results and GENESIS results for all simulations with a single groin as well as perfect symmetry between the positive and negative wave angle forcing.

• Figures 40-41
• 

  Figure 40. Calculated (a) shoreline position, (b) shoreline change, and (c) mean net transport for straight shoreline with single groin; H0 = 0.75 m, T = 8 sec, θ0 = +15-deg.

• 

  Figure 41. Calculated (a) shoreline position, (b) shoreline change, and (c) mean net transport for straight shoreline with single groin; H0 = 0.75 m, T = 8 sec, θ0 = -15-deg.

Detached breakwater

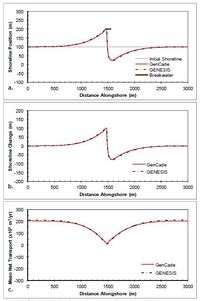
A detached breakwater case is evaluated in this section with a 90 m long emergent breakwater at the center of the domain located 100 m offshore of the shoreline at a depth of 6 m. Although this case is similar in configuration to the LSTF experiment detailed in section 3.1, this case is simulated at full prototype (i.e., larger) scale and over a much longer time frame. Figure 42 shows the results after a 2-year simulation with constant +15-deg wave angle forcing. These simulations result in a nearly symmetric shoreline change response in the lee of the breakwater and the development of a large salient approximately 75 m at the apex. The transport rates decrease from a background rate of 200,000 m3/yr to approximately 25,000 m3/yr directly behind the breakwater structure. Figure 43 presents the results after a 2-year simulation with constant -15-deg wave angle forcing. The opposite pattern is observed in this example because transport is forced by negative wave angles relative to shore normal. Figure 43(c) shows that an increase in transport occurs on the left(downdrift) side of the breakwater from -200,000 m3/yr background transport rate to -25,000 m3/yr in the lee of the breakwater. Again, the expected opposite shoreline response is observed here. Figures 42 and 43 show good overall agreement between GenCade results and GENESIS results. There is some difference observed at the peaks of the salient and the downdrift erosional zones; however, this difference is small and accounts for only about two percent error (1.7 percent normalized mean absolute error and 2.3 percent normalized root-mean-square error). Differences in results could be because of differences in the wave transformation model.

• Figures 42-43
• 

  Figure 42. Calculated (a) shoreline position, (b) shoreline change, and (c) mean net transport for straight shoreline with detached breakwater; H0 = 0.75 m, T = 8 sec, θ0 = +15-deg.

• 

  Figure 43. Calculated (a) shoreline position, (b) shoreline change, and (c) mean net transport for straight shoreline with detached breakwater; H0 = 0.75 m, T = 8 sec, θ0 = -15-deg.

T-groin

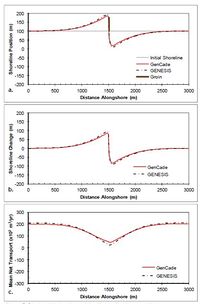
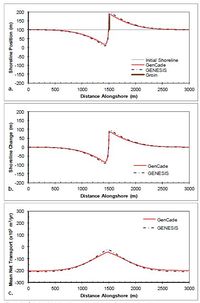
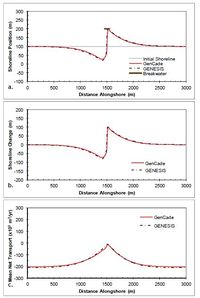
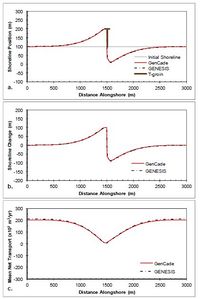
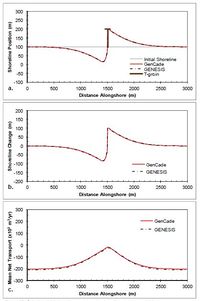
A T-groin case is demonstrated in this section with a 90 m long T-head groin at the center of the domain located 100 m offshore of the shoreline with all diffracting tips set to a depth of 6 m. Figure 44 shows the results after a 2-year simulation with constant +15-deg wave angle forcing. These simulations result in a nearly symmetric shoreline change response in the lee of the T-head and on either side of the groin and the accretion of shoreline out to the structure tip. The transport rates decrease from a background rate of 200,000 m3/yr to zero directly adjacent to the groin structure.Figure 45 presents the results after a 2-year simulation with constant -15-deg wave angle forcing. The opposite pattern is again observed in this example because transport is forced by negative wave angles relative to shore normal. Figure 45(c) shows that an increase in transport occurs on the left (downdrift) side of the groin from -200,000 m3/yr background transport rate to zero directly adjacent to the groin structure. Figures 44 and 45 show good agreement between GenCade results and GENESIS results over the entire length of the domain.

• Figures 44-45
• 

  Figure 44. Calculated (a) shoreline position, (b) shoreline change, and (c) mean net transport for straight shoreline with T-head groin; H0 = 0.75 m, T = 8 sec, θ0 = +15-deg.

• 

  Figure 45. Calculated (a) shoreline position, (b) shoreline change, and (c) mean net transport for straight shoreline with T-head groin; H0 = 0.75 m, T = 8 sec, θ0 = -15-deg.

Seawall

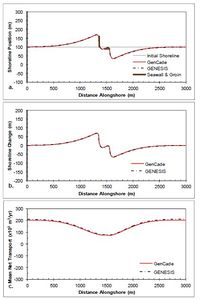
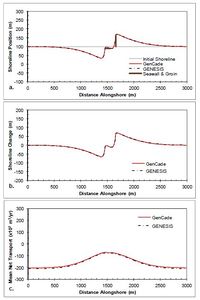
A seawall case is demonstrated next with a simple 100 m long seawall at the center of the domain located 10 m shoreward of (i.e., behind) the shoreline. Since a seawall that lies behind a straight shoreline with no other structures will never become exposed, a groin was added 100 m updrift of the seawall to force shoreline erosion in the vicinity of the seawall and expose the seawall to influence downdrift shoreline evolution. The groin follows the same dimensions of the single groin case. Figure 46 shows the results after a 2-year simulation with constant +15-deg wave angle forcing. The shoreline erodes to the right of the groin exposing the seawall. This halts erosion at the seawall, but accelerates erosion to the right (downdrift) of the seawall. Prior to the end of the simulation sediment accretes in front of the seawall resulting in the shoreline position observed in Figure 46(a).Figure 47 presents the results after a 2-year simulation with constant -15- deg wave angle forcing. In this case the groin was again placed updrift of the seawall, but since the wave angle is reversed, the groin is now 10 m to the right (updrift) of the seawall. Figures 46 and 47 again show excellent agreement between GenCade results and GENESIS results over the entire length of the domain.

• Figures 46-47
• 

  Figure 46. Calculated (a) shoreline position, (b) shoreline change, and (c) mean net transport for straight shoreline with seawall and groin; H0 = 0.75 m, T = 8 sec, θ0 = +15-deg.

• 

  Figure 47. Calculated (a) shoreline position, (b) shoreline change, and (c) mean net transport for straight shoreline with seawall and groin; H0 = 0.75 m, T = 8 sec, θ0 = -15-deg.

Beach fill

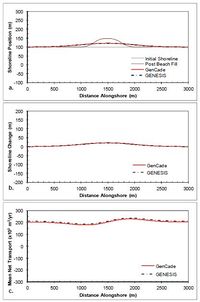
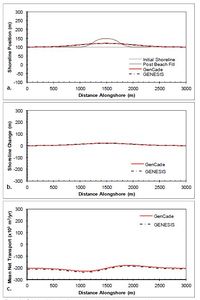
The simple case of a straight shoreline without any coastal structures is again presented in this section, but in this case a beach fill is added to evaluate shoreline progradation during the fill and the diffusion of the material and shoreline evolution after beach fill project completion. The beach fill project was initiated two months into the simulation and involved a construction duration of two months adding 50 m of berm width over an alongshore distance of 500 m. Upon beach fill completion (i.e., after two months of pumping fill onto the berm), no additional material was added. Figure 48 shows the results after a two-year simulation with constant +15-deg wave angle forcing. Figure 48(a)shows the shoreline position immediately after the fill project as well as the shoreline position after two years (i.e., 20-months after completion of the fill project). This clearly shows the lateral diffusion of the beach fill material along the shoreline. Figure 48(c) shows the transport gradient around the beach fill berm feature with the greatest deviation from background transport rate occurring at the fill transition zones. Figure 49 shows the results after a two-year simulation with constant -15-deg wave angle forcing. As one should expect, the shoreline evolution is identical to that shown in Figure 48 and only the transport rates are inverted. Results for all simulations with beach fills result in close agreement between GenCade results and GENESIS results.

• Figures 48-49
• 

  Figure 48. Calculated (a) shoreline position, (b) shoreline change, and (c) mean net transport for straight shoreline with a beach fill; H0 = 0.75 m, T = 8 sec, θ0 = +15-deg.

• 

  Figure 49. Calculated (a) shoreline position, (b) shoreline change, and (c) mean net transport for straight shoreline with a beach fill; H0 = 0.75 m, T = 8 sec, θ0 = -15-deg.

Inlet

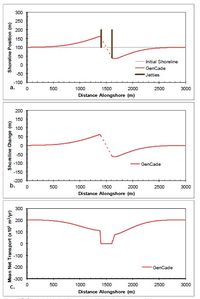
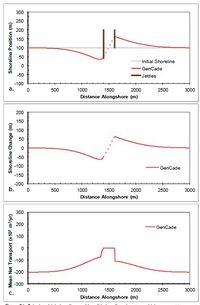
A case with a single inlet centered along a straight shoreline is demonstrated with GenCade in this section. The idealized inlet is 200 m wide and is stabilized with two 200 m jetties with bypassing coefficients set to 1.0 permeability set to 0.0, and diffracting tip depth set to 7 m. All morphological elements are set to equilibrium. The attachment bars spread bypassing across five cells (50 m) starting immediately adjacent to each of the jetties. Figure 50 shows the results after a two-year simulation with constant +15-deg wave angle forcing. This simulation results in an updrift offset inlet configuration that is typical of inlets associated with adequate updrift sediment supply and moderate transport rates. The development of an updrift fillet and downdrift erosion is observed in the shoreline response. The transport rates decrease from a background rate of 200,000 m3/yr to approximately 100,000 m3/yr adjacent to the jetty, then immediately drop to zero inside the inlet. Figure 51 shows the results after a two-year simulation with constant -15-deg wave angle forcing. The opposite pattern is observed in this example because transport is forced by negative wave angles relative to shore normal. Figure 51(c) shows that the transport rates increase from a background rate of -200,000 m3/yr to approximately -100,000 m3/yr adjacent to the jetty, then immediately rise to zero inside the inlet. Again,the expected opposite shoreline response is observed here. No comparison was developed for GENESIS because inlets, shoal evolution, and bypassing are new capabilities only incorporated in GenCade. Sediment transport and bypassing within the inlet are calculated within the inlet reservoir module of GenCade. Figure 52 shows the ebb and flood tidal delta evolution for these simulations compared to the shoal evolution in the same cases with 100,000 m3/yr after 2.5 years, 200,000 m3/yr after 5.5 years, and 50,000 m3/yr after 9.5 years dredged from the ebb shoal and with 150,000 m3/yr after seven years dredged from the flood shoal.

• Figures 50-52
• 

  Figure 50. Calculated (a) shoreline position, (b) shoreline change, and (c) mean net transport for straight shoreline with an inlet; H0 = 0.75 m, T = 8 sec, θ0 = +15-deg.

• 

  Figure 51. Calculated (a) shoreline position, (b) shoreline change, and (c) mean net transport for straight shoreline with an inlet; H0 = 0.75 m, T = 8 sec, θ0 = +15-deg.

• 

  Figure 52. Calculated ebb and flood shoal evolution.