Rubble Mounds
Representation of Rubble Mound Structures in the Coastal Modeling System
By Christopher Reed and Alejandro Sánchez
Last Modified: September 17, 2010
Purpose
This Coastal and Hydraulics Engineering Technical Note (CHETN) describes the representation of rubble mound structures in the Coastal Modeling System (CMS) operated through the Surface-water Modeling System (SMS) (Zundel, 2000). The CMS is a hydrodynamic and transport model designed for coastal and inlet applications, and the SMS is a graphical user interface utility for PCs as developed by the U.S. Army Corps of Engineers (USACE). The simulation of rubble mounds has been implemented in the CMS-Flow explicit solver. The mathematical and numerical implementation is described and the results of the model verification presented. The sensitivity of the model coefficients is determined for a typical range of parameter values.
Introduction
Rubble mound structures are a common coastal engineering structure used for shoreline protection and flow and sediment transport control. They are typically used as seawalls, groins, breakwaters and jetties. The design of rubble mound structures often consists of a core of small to medium size rock or riprap covered with larger rock or riprap to armor against wave energy. In coastal modeling, it is usually reasonable to assume that the flow through these structures is negligible, and they are represented as solid structures, impermeable to both flow and sediment transport. However, some rubble mounds such as that of Dana Point, CA are designed with a sufficiently large diameter core material to allow for flow and fine sediments to pass through and coarser sediment to be trapped within.
Since permeable rubble mounds are a significant control of the hydrodynamic and sediment transport in the coastal zone, it is important to include them in the CMS. An algorithm is developed based on the Forchheimer equation (1901), which represents the introduction of a non-linear term in the Darcy equation for porous media. Both the linear and non-linear coefficients in the equation are evaluated using data from studies by Gent (1995) and Sidiropoulou et al. (2007). The structures are implemented within the CMS framework by extending the steady flow equation of Forchheimer to the unsteady shallow water equations. The CMS is verified by comparing the model output to results of analytical solutions for steady flow cases. A sensitivity analysis was also conducted to determine the sensitivity of the rubble mound simulations to uncertainty in the input parameter values.
Coastal Modeling System
The CMS calculates water levels, currents and waves through the coupling between a hydrodynamic model, CMS-Flow and a wave spectral model, CMS-Wave. These two models can also interact dynamically to simulate sediment and salinity transport, and morphology change (Militello, et al., 2004; Buttolph et al. 2006; Lin et al. 2008).
CMS‑Flow is a three-dimensional (3D) finite-volume model that solves the mass conservation and shallow-water momentum equations of water motion. The model can run in a two-dimensional (2-D) mode based on the depth-integrated equation. The wave radiation stress and wave field information entering the flow and sediment transport formulas in CMS‑Flow are supplied by CMS‑Wave. CMS‑Flow is forced by water surface elevation (e.g., from tide), wind and river discharge at the model boundaries, and wave radiation stress and wind field over the model computational domain. Physical processes pertinent to the present study calculated by CMS‑Flow include current, water surface elevation, sediment transport, morphology change, and representation of non-erodible bottom (e.g., reef). Additional capabilities include wetting and drying, spacially varying bottom friction, salinity transport, efficient grid storage in memory, and hot-start options.
CMS‑Wave is a 2-D steady-state (time-independent) phase-averaged, spectral wave transformation model. The model contains theoretically derived approximations of wave diffraction, reflection, and wave-current interaction for wave simulations at coastal inlets with jetties and breakwaters. It employs a forward-marching and finite-difference method to solve the wave action conservation equation. CMS-Wave operates mainly on a coastal half-plane, so primary waves can propagate only from the seaward boundary toward shore. In the full-plane mode, CMS‑Wave performs the backward-marching for seaward spectral transformation after the forward-marching is completed.
Representation of Rubble Mound Structures
The Forchheimer equation is conventionally written for unidirectional flow as,
| (1) |
where is the hydraulic gradient, is the bulk velocity and and are dimensional coefficients. The first and second terms on the right hand side represent the laminar and turbulent components of flow resistance. In order to incorporate the resistance equation in to the CMS governing equations, Fochheimer’s equation is cast into a format compatible with the steady state shallow water wave equations. In this form, the equations represents a balance between the hydraulic gradient and drag. The formulation can be extended to general applications by adding the following resistance terms to the x and y momentum equations:
| and | (2) |
where is the acceleration due to gravity, and are the water volume fluxes with unit width, and are the bulk current velocities in the x and y directions.
There are two other modifications to the original CMS governing equations to simulate the effects of the rubble mound. In the mass conservation equation, the rubble mound void space (i.e. porosity) is introduced. The revised equation is:
| (3) |
Similarly, in the morphology simulation, the equation for the change in bed elevation is revised to account for the rubble mound void space:
| (4) |
where is the bed elevation, is the sediment porosity, and are the bedload fluxes in the x and y directions, is the erosion flux and is the depositional flux.
Numerical Implementation
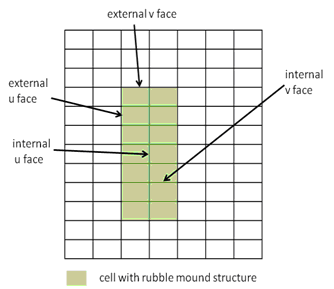
The CMS-Flow model uses a staggered grid for the bases of the numerical solution. Figure 1 shows a typical grid with a set of cells marked as containing a rubble mound structure. The momentum is calculated at the cell faces. For the purpose of implementing the rubble mound representation in the numerical solution algorithm, the faces are designated as external or internal as noted in Figure 1. The rubble mound resistance formulations are added to the x- and y-direction momentum equations for all internal and external faces. In general, the same numerical approximation conventions used for evaluating variables and gradients in the standard faces and can be found in the CMS documentation (Militello et al., 2004).
In the numerical solution, the effects of wind and wave radiation stress gradients are eliminated for all rubble mound cells. There are no additional modifications to the sediment transport algorithms, other than that noted in equation 5. Bedload can be transported into a rubble mound cell. Transport within a rubble mound cell will be greatly reduced by the lower flow speed, reduced energy and subsequent lower bottom stresses.
The rubble mound is specified in the CMS by identifying the cells containing the rubble mound structure, and specifying the structure porosity, nominal riprap or rock diameter, and the method for specifying resistance coefficients a and b.
A model test case was developed to both verify the model code and to determine the sensitivity to the grid resolution used to represent the rubble mound. A schematic of the test case is shown in Figure 2. Water levels are held constant at the upstream and downstream values, creating the gradient across the rubble mound. The gradient creates a flow that is dependent on Δh, L and the resistance parameters a and b. Five CMS grids were constructed to represent the test case, each using a different number of cells to represent the rubble mound. For each grid scenario, a simulation was made sufficiently long to reach steady conditions. Then the flow rate through the mound was compared to an analytical solution. Analytical solutions can be readily obtained from the resistance formula for the test case configuration if either a or b is set to zero.
The results for the 5 test grids are shown in Table 1 for b=0, and in table 2 for a=0. For all of the simulations, du was set to 2.0 m, dL was set to 1.5 m, L ~16 m and the values for a and b were 1.0 and 1.0. The total length of the grid was 160 meters, and the rubble mound was placed in the center. The precise value for L in each test case depended on the actual cell width. For the smaller cell widths (Cases 1 and 2) a variable spaced grid was used and the SMS algorithm for creating the grid did not yield the specified spacing exactly. These differences are noted in the tables and were incorporated into the analytical solutions.
The comparison is very good, with the maximum difference between the simulated and analytical solution for all cases less than 0.12 percent. These tests confirm a valid implementation of the Forchheimer resistance formula into the CMS and demonstrate the grid independence of the solution. The grid independence was a direct consequence of the special numerical differencing applied to the external faces.
Figure 2 Schematic of the model configuration for validation and numerical grid independence test.
Table 1 Results of Validation and Grid Size Independence for a=1.0, b=0.0
| # cells |
Cell Width (m) | L (m) | a (s/m) | b (s2/m2) | 'qx '(m2/s) (theoretical) | qx (m2/s) (numerical) | %-error |
| 16 | 0.981 | 15.7 | 0 | 10 | 0.0991 | 0.0991 | -0.02 |
| 8 | 1.961 | 15.7 | 0 | 10 | 0.0991 | 0.0991 | -0.05 |
| 4 | 4 | 16 | 0 | 10 | 0.0982 | 0.0981 | -0.04 |
| 2 | 8 | 16 | 0 | 10 | 0.0982 | 0.0981 | -0.07 |
| 1 | 16 | 16 | 0 | 10 | 0.0982 | 0.0981 | -0.11 |
Table 2 Results of Validation and Grid Size Independence for a=0.0, b=10.0
| # cells |
Cell Width (m) | L (m) | a (s/m) | b (s2/m2) | 'qx '(m2/s) (theoretical) | qx (m2/s) (numerical) | %-error |
| 16 | 0.981 | 15.7 | 1 | 0 | 0.0557 | 0.0557 | -0.01 |
| 8 | 1.961 | 15.7 | 1 | 0 | 0.0557 | 0.0557 | -0.01 |
| 4 | 4 | 16 | 1 | 0 | 0.0547 | 0.0547 | -0.01 |
| 2 | 8 | 16 | 1 | 0 | 0.0547 | 0.0547 | -0.01 |
| 1 | 16 | 16 | 1 | 0 | 0.0547 | 0.0547 | -0.01 |
Specifying the Resistance Coefficients a and b:
The coefficients in Fochheimer’s resistance equation have been evaluated in a number of studies. Sidiropoulou et al. (2006) provides a review of proposed formulas. The formulas by Ward (1964) are:
where is the water dynamic viscosity and is the riprap or rock diameter. Kadlec and Knight (1996) suggested the following formulas:
Sidiropoulou et al. (2006) empirically derived:
A plot of these functions for a porosity of 0.4 and a range of diameters from 0.05 to 1.0 meters is shown in Figure 3 and 4. The largest variation in values occurs for the smaller rock size for coefficient a. The variation for parameter b is smaller, less than a factor of two over the range of rock sizes considered.
Figure 3 Dependence of Forchheimer’s coefficient a on rock size (porosity of 0.4 )
Figure 4 Dependence of Forchheimer ’s coefficient b on rock size (porosity of 0.4 )
Sensitivity Analysis
These coefficients in the equations for the Forchheimer coefficients presented above have been determined from fitting the equations to various data sets, and it is not clear if one set is better than any other for a given application. In order to assess the sensitivity of CMS simulation results to the different a and b values from the different formulas, a sensitivity analysis has been conducted. The tests consisted of a proto-type scale simulation of flow past a rubble mound structure on a mildly sloping bed. The CMS grid configuration is shown in Figure 5, which corresponds to the validation configuration using 8 cells for representing the rubble mound. The upstream water depth was set to 2.0 m and the downstream depth to 1.5 m. An example of the typical flow and water surface elevation is shown in Figure 6
Figure 5 CMS model configuration for the sensitivity analysis
Figure 6 Typical simulation results for a CMS model sensitivity scenario
The sensitivity scenarios and the results are shown in Table 3. The scenarios represent 5 different riprap or rock sizes. For all scenarios the void space (i.e porosity) was set to 0.4. The corresponding values for a and b were selected using the formulas of Ward (1994), Kadlec and Knight (1996) and Sidiropoulou et al. (2006). For each scenario the steady flow rate resulting from the simulation was recorded and is shown in Table 3.
Table 3 Results of the sensitivity analysis
| Rock Size (m) | Source | a (s/m) | b (s2/m2) | q (m2/s) | L/T* Ratio | variation % |
| 0.05 | Ward | 0.0100 | 21.0 | 0.068 | 1.4 | 34.0 |
| Kadlec & Knight | 0.1000 | 38.0 | 0.049 | 10.8 | ||
| Sidiropoulou | 0.2800 | 24.0 | 0.054 | 42.8 | ||
| 0.1 | Ward | 0.0026 | 10.6 | 0.096 | 0.5 | 29.6 |
| Kadlec & Knight | 0.0260 | 19.0 | 0.071 | 3.9 | ||
| Sidiropoulou | 0.0990 | 10.2 | 0.090 | 21.6 | ||
| 0.2 | Ward | 0.0007 | 5.3 | 0.136 | 0.2 | 34.9 |
| Kadlec & Knight | 0.0065 | 9.6 | 0.101 | 1.3 | ||
| Sidiropoulou | 0.0350 | 4.2 | 0.145 | 11.4 | ||
| 0.3 | Ward | 0.0003 | 3.6 | 0.166 | 0.1 | 44.8 |
| Kadlec & Knight | 0.0029 | 6.4 | 0.124 | 0.7 | ||
| Sidiropoulou | 0.0190 | 2.5 | 0.196 | 7.7 | ||
| 0.5 | Ward | 0.0001 | 2.1 | 0.214 | 0.0 | 49.5 |
| Kadlec & Knight | 0.0010 | 3.8 | 0.160 | 0.3 | ||
| Sidiropoulou | 0.0089 | 1.3 | 0.266 | 5.0 |
*L/T Ratio is the ratio between the laminar and turbulent resistance terms
The results indicate a moderate sensitivity to the values of a and b selected for each riprap or rock size. The flow rate through the rubble mound increases with increasing riprap or rock size. For all three formulas, the ratio of the laminar to turbulent resistance force decreases with increasing riprap or rock size, and the ratios tend to be significantly higher for the Siridopoulou (2006) formulation. The percent variation in the simulated flow rate, defined as the maximum difference divided by the average flow rate, increases with increasing riprap or rock size.
The data used to develop the recommended parameter values were typically based on laboratory experiments with rubble mound rock sizes in the range of 1 to 3 cm. The maximum size used in the experiments was 8 cm. Thus for riprap or rock size values that are typical of coastal engineering structures, the values of a and b from formulas of Ward (1964), Kadlec and Knight (1996) and Siridopoulou (2006) represent an extension beyond the rock sizes representing the experimental data base.
Conclusions
A representation of rubble mound structures has been implemented in the explicit version of the CMS Flow model. The model is based on the Forchheimer’s resistance formulation with accounts for both laminar and turbulent flow resistance in the flow through the rubble mound. Implementation of the approach in the CMS code was validated and shown to have excellent grid-size independence. A sensitivity test was conducted to determine the sensitivity of the simulations for two of the model parameters, resistance coefficients a and b. The sensitivity was shown to be moderate over a range of parameter values. The simulated flow rates varied from 30% to 50% when using parameter values selected from the range of recommended values.
Additional Information
This techical wiki was prepared and funded under the Coastal Inlets Research Program (CIRP) being conducted a the U.S. Army Engineer Research and Development Center, Costal and Hydraulics Laboratory. Questions about this technical note can be addressed to to Dr. Christopher W. Reed (Chris_Reed@URSCorp.com) of URS Corporation or Alejandro Sanchez (Alejandro.Sanchez@usace.army.mil). The CIRP Program Manager, Dr. Julie D. Rosati (Julie.D.Rosati@usace.army.mil), the assistant Program Manager, Dr. Nicholas C. Kraus (Nicholas.C.Kraus@usace.army.mil).
References
- Buttolph, A. M., C. W. Reed, N. C. Kraus, N. Ono, M. Larson, B. Camenen, H. Hanson, T. Wamsley, and A. K. Zundel, A. K. 2006. Two-dimensional depth-averaged circulation model CMS-M2D: Version 3.0, Report 2, sediment transport and morphology change. Coastal and Hydraulics Laboratory Technical Report ERDC/CHL-TR-06-7. Vicksburg, MS: U.S. Army Engineer Research and Development Center.
- Forchheim, Ph. "Wasserbevegung durch Boden" , Z. Ver. Deutsh. Ing., Vol. 45, 1901, p.1781-1788
- Kadlec H.R., Knight, L.R., 1996. Treatment Wetlands. Lweis Publishers.
- Melina G. Sidiropoulou Konstadinos N. Moutsopoulos Vassilios A. Tsihrintzis (2007). Determination of Forchheimer equation coefficients a and b. Hydrological Processes, Volume 21, Issue 4, 15, Pages: 534–554.
- Militello, A., Reed, C.W., Zundel, A.K., and Kraus, N.C. 2004. Two-Dimensional Depth-Averaged Circulation Model M2D: Version 2.0, Report 1, Technical Documentation and User’s Guide, ERDC/CHL TR-04-2, U.S. Army Research and Development Center, Coastal and Hydraulics Laboratory, Vicksburg, MS.
- Ward, J.C., 1964. Turbulent flow in porous media. Journal of Hydrualic Division, ASCE 90(5): 1-12