GenCade:Internal Wave Transformation

Note: The Wave Calculation page introduces the internal wave transformation topic within GenCade.

Breaking Waves

Wave transformation from the deep water reference depth or the nearshore reference line (depending on whether or not the external wave model is used) is initially conducted without accounting for diffraction from structures located in the model reach. The solution strategy is to obtain a first approximation of breaking wave conditions without including diffraction and then modify the result by accounting for changes to the wave field by each diffraction source.

Omitting diffraction, there are three unknowns in the breaking wave calculation: the wave height, angle, and the depth at breaking. Three equations are needed to obtain these quantities, which are introduced below. These are the equation for the breaking wave height based on reference wave data, a depth-limited breaking criterion, and a wave refraction equation (Snell’s law).

The height of breaking waves that are transformed by refraction and shoaling are calculated as:

$H_{b}=K_{R}K_{S}H_{Ref}$

where $H_{b}$ is the breaking wave height, $K_{R}$ is the refraction coefficient, $K_{S}$ is the shoaling coefficient, and $H_{Ref}$ is the wave height at the offshore reference depth or the nearshore reference line depending on which wave model is used. Both $K_{R}$ and $K_{S}$ are calculated in the classical way:

$K_{R}={\sqrt {\frac {cos\theta _{1}}{cos\theta _{2}}}}$ and $K_{S}={\sqrt {\frac {C_{g1}}{C_{g2}}}}$

where $cos\theta _{1}$ is the starting angle of the ray and $cos\theta _{2}$ is the angle of arrival at $P_{2}$, the location of which is determined by the breaking depth, and $C_{g1}$ and $C_{g2}$ are the group velocities at their respective depths (meters/second).

The equation for depth-limited wave breaking is given by:

$H_{b}=\gamma d_{b}$

where $\gamma$ is 0.78. If there are no structures to produce diffraction, the undiffracted wave characteristics are used as input to the sediment transport relation (see Sand Transport Rates). If such obstacles are present, breaking wave heights and directions are recalculated, as described next.

Breaking Waves Affected by Structures

Structures such as detached breakwaters, jetties, and groins which extend well seaward of the surf zone intercept the incident waves prior to breaking. Headlands and islands (specified as structures in GenCade) may also intercept waves. In the following discussion, all such objects are referred to as structures. Each tip of a structure will produce a near- circular wave pattern, and this distortion of the wave field is a significant factor controlling the response of the shoreline in the lee of the structure. Sand typically accumulates in the diffraction shadow of a structure, being transported from one or both sides by the oblique wave angles in the circular wave pattern and the decrease in wave height alongshore with penetration into the shadow region. Accurate and efficient calculation of waves transforming under combined diffraction, refraction, and shoaling to break is required to obtain realistic predictions of shoreline change in such situations.

Figure 1 is a definition sketch of the calculation procedure for the breaking wave height and angle behind a structure (Kraus 1981, 1982, 1984). Conceptually, the area of interest is separated into a shadow region and an illuminated region by a wave ray directed toward the beach from the tip of the structure at the same angle as the incident waves arriving at the tip. To determine the breaking wave height, a diffraction coefficient must be calculated in both regions because the diffraction effect can extend far into the illuminated region. To determine the breaking wave angle inside the shadow region, wave rays are assumed to proceed radially from the tip of the structure $P_{1}$ at an angle $\theta _{1}$ to arrive at some point $P_{2}$ with an angle $\theta _{2}$, where they break.

Figure 1. Definition Sketch for the Wave Diffraction Calculation

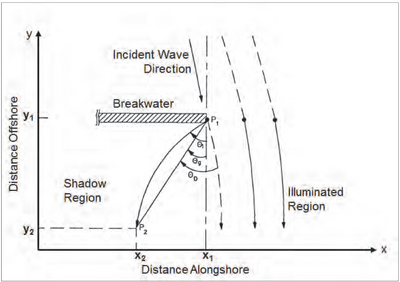
The angle $\theta _{1}$ at which a wave ray must start to arrive at $P_{2}$ inside the shadow region is not known prior since it is a function of the breaking criterion as well as the distance alongshore defining the location of grid cells in the numerical calculation. A ray shooting technique can be used to determine $\theta _{1}$ (Kraus 1982, 1984), but this procedure is complex and requires considerable execution time. As a first approximation, the geometric angle $\theta _{g}$ defined by the straight line between $P_{1}$ and $P_{2}$ is used.

Due to the impact of diffraction, the wave height is reduced and, thus, the wave is not breaking. An iterative procedure is used to find the location where the wave, which has been transformed by diffraction, refraction, and shoaling, is breaking. At breaking, the wave fulfills the two conditions:

$H_{b}=K_{D}\theta _{D}H'_{b}$ and $H_{b}=\gamma d_{b}$

Where $K_{D}$ is a diffraction coefficient, $\theta _{D}$ is the angle between the incident wave ray at $P_{1}$ and a straight line between $P_{1}$ and $P_{2}$, if $P_{2}$ is in the shadow region, $H'_{b}$ is the breaking wave height at the same cell without diffraction.

For waves that are inside two overlapping shadow zones, an average $\theta _{g}$ is calculated together with a composite $K_{d}$ coefficient for the two diffracting systems. Then, the same iteration procedure as the one used inside one diffraction system is used. In the illuminated region a similar procedure is used, where a composite $K_{d}$ is used, but instead of a $\theta _{g}$, the undiffracted wave direction is used.

Because GenCade was developed to simulate waves and shoreline change in the field, the procedure of Goda et al. (1978) (see also, Goda (1984)) was adapted. Details of application of the method to calculate wave breaking produced by combined diffraction, refraction, and shoaling as used in GenCade are given by Kraus (1981, 1982, 1984, 1988). For given wave conditions at the diffracting tip, the diffraction coefficient is only a function of $\theta _{D}$. In GenCade, it is assumed that the method is valid for relatively short structures such as detached breakwaters.

Smoothed Nearshore Contour - ISMOOTH

A basic assumption in the formulation of the shoreline change model is that the profile moves parallel to itself. As a consequence, bottom contours would move parallel to the shoreline. If this assumption is applied directly in the internal wave model, unrealistic wave transformation can result in regions where the shoreline position changes relatively abruptly, possibly leading to numerical instability. The use of the smoothed contour recognizes that the shoreline evolution feeds back on the nearshore bathymetry without having to be a direct replica of the shoreline.

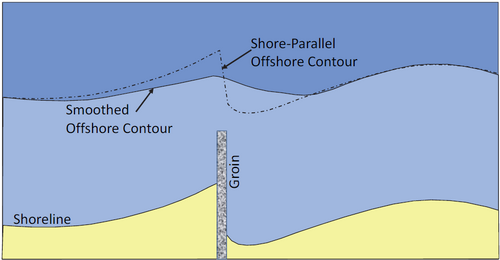
GenCade uses a smoothed bottom contour in performing the internal wave calculation, as illustrated in Figure 2. In this figure, the shore-parallel contour shown changes radically at the groin. The smoothed contour is expected to better represent the offshore bathymetry. The smoothed contour shape is calculated as a running average using a window size containing the number of cells as specified by the input parameter ISMOOTH. A larger value of ISMOOTH will result in an offshore contour that has less curvature. An extreme case of ISMOOTH = 1 would result in an offshore contour that would be parallel to the shoreline (as the dash-dotted line in Figure 2) whereas ISMOOTH = N would result in a straight contour line parallel to the x-axis. ISMOOTH must always be a positive, odd number. If an even number is entered for ISMOOTH, the model automatically resets the value of ISMOOTH to equal ISMOOTH-1 (and therefore an odd number). If a negative value is entered for ISMOOTH, the model automatically resets the value of ISMOOTH to equal 1.

At the lateral boundaries (i.e., X=1 and X=N), the moving average calculates values less than: [(ISMOOTH -1)/2] by interpolation from the boundary value to the first smoothed value. The calculated contour is assumed to be representative for all contour lines between the input wave depth and the undiffracted wave breaking depth. The shape of the representative offshore contour is recalculated continuously using the shoreline position at that time. It is recommended that the user vary the ISMOOTH value to obtain a more realistic shoreline evolution. Too small values often lead to large angles between the waves and the shoreline which may produce unrealistic transport directions.

Figure 2. Example of smoothed offshore bottom contour

Pre-Specified Regional Contour

Insert Section Text Here

Useful Links

GenCade References

GenCade Home Page

GenCade Documentation Portal