Rubble Mound Tests
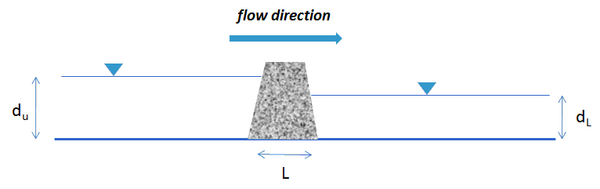
A model test case was developed to both verify the model code and to determine the sensitivity to the grid resolution used to represent the rubble mound. A schematic of the test case is shown in Figure 1. Water levels are held constant at the upstream and downstream values, creating the gradient across the rubble mound. The gradient creates a flow that is dependent on Δh, L and the resistance parameters a and b. Five CMS grids were constructed to represent the test case, each using a different number of cells to represent the rubble mound. For each grid scenario, a simulation was made sufficiently long to reach steady conditions. Then the flow rate through the mound was compared to an analytical solution. Analytical solutions can be readily obtained from the resistance formula for the test case configuration if either a or b is set to zero.
| (1) |
The results for the 5 test grids are shown in Table 1 for b=0, and in table 2 for a=0. For all of the simulations, du was set to 2.0 m, dL was set to 1.5 m, L ~16 m and the values for a and b were 1.0 and 1.0. The total length of the grid was 160 meters, and the rubble mound was placed in the center. The precise value for L in each test case depended on the actual cell width. For the smaller cell widths (Cases 1 and 2) a variable spaced grid was used and the SMS algorithm for creating the grid did not yield the specified spacing exactly. These differences are noted in the tables and were incorporated into the analytical solutions.
The comparison is very good, with the maximum difference between the simulated and analytical solution for all cases less than 0.12 percent. These tests confirm a valid implementation of the Forchheimer resistance formula into the CMS and demonstrate the grid independence of the solution. The grid independence was a direct consequence of the special numerical differencing applied to the external faces.
Table 1. Results of Validation and Grid Size Independence for a=1.0, b=0.0
| # cells |
Cell Width (m) | L (m) | a (s/m) | b (s2/m2) | 'qx '(m2/s) (theoretical) | qx (m2/s) (numerical) | %-error |
| 16 | 0.981 | 15.7 | 0 | 10 | 0.0991 | 0.0991 | -0.02 |
| 8 | 1.961 | 15.7 | 0 | 10 | 0.0991 | 0.0991 | -0.05 |
| 4 | 4 | 16 | 0 | 10 | 0.0982 | 0.0981 | -0.04 |
| 2 | 8 | 16 | 0 | 10 | 0.0982 | 0.0981 | -0.07 |
| 1 | 16 | 16 | 0 | 10 | 0.0982 | 0.0981 | -0.11 |
Table 2. Results of Validation and Grid Size Independence for a=0.0, b=10.0
| # cells |
Cell Width (m) | L (m) | a (s/m) | b (s2/m2) | 'qx '(m2/s) (theoretical) | qx (m2/s) (numerical) | %-error |
| 16 | 0.981 | 15.7 | 1 | 0 | 0.0557 | 0.0557 | -0.01 |
| 8 | 1.961 | 15.7 | 1 | 0 | 0.0557 | 0.0557 | -0.01 |
| 4 | 4 | 16 | 1 | 0 | 0.0547 | 0.0547 | -0.01 |
| 2 | 8 | 16 | 1 | 0 | 0.0547 | 0.0547 | -0.01 |
| 1 | 16 | 16 | 1 | 0 | 0.0547 | 0.0547 | -0.01 |
Sensitivity Analysis
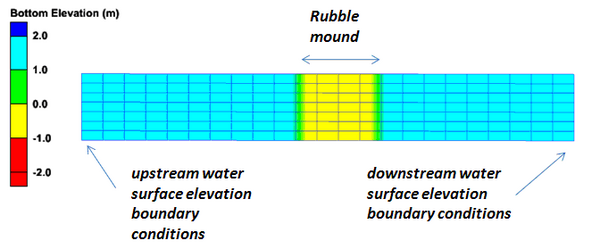
These coefficients in the equations for the Forchheimer coefficients presented above have been determined from fitting the equations to various data sets, and it is not clear if one set is better than any other for a given application. In order to assess the sensitivity of CMS simulation results to the different a and b values from the different formulas, a sensitivity analysis has been conducted. The tests consisted of a proto-type scale simulation of flow past a rubble mound structure on a mildly sloping bed. The CMS grid configuration is shown in Figure 2, which corresponds to the validation configuration using 8 cells for representing the rubble mound. The upstream water depth was set to 2.0 m and the downstream depth to 1.5 m. An example of the typical flow and water surface elevation is shown in Figure 3.
The sensitivity scenarios and the results are shown in Table 3. The scenarios represent 5 different riprap or rock sizes. For all scenarios the void space (i.e porosity) was set to 0.4. The corresponding values for a and b were selected using the formulas of Ward (1994), Kadlec and Knight (1996) and Sidiropoulou et al. (2006). For each scenario the steady flow rate resulting from the simulation was recorded and is shown in Table 3.
Table 3. Results of the sensitivity analysis
| Rock Size (m) | Source | a (s/m) | b (s2/m2) | q (m2/s) | L/T* Ratio | variation % |
| 0.05 | Ward | 0.0100 | 21.0 | 0.068 | 1.4 | 34.0 |
| Kadlec & Knight | 0.1000 | 38.0 | 0.049 | 10.8 | ||
| Sidiropoulou | 0.2800 | 24.0 | 0.054 | 42.8 | ||
| 0.1 | Ward | 0.0026 | 10.6 | 0.096 | 0.5 | 29.6 |
| Kadlec & Knight | 0.0260 | 19.0 | 0.071 | 3.9 | ||
| Sidiropoulou | 0.0990 | 10.2 | 0.090 | 21.6 | ||
| 0.2 | Ward | 0.0007 | 5.3 | 0.136 | 0.2 | 34.9 |
| Kadlec & Knight | 0.0065 | 9.6 | 0.101 | 1.3 | ||
| Sidiropoulou | 0.0350 | 4.2 | 0.145 | 11.4 | ||
| 0.3 | Ward | 0.0003 | 3.6 | 0.166 | 0.1 | 44.8 |
| Kadlec & Knight | 0.0029 | 6.4 | 0.124 | 0.7 | ||
| Sidiropoulou | 0.0190 | 2.5 | 0.196 | 7.7 | ||
| 0.5 | Ward | 0.0001 | 2.1 | 0.214 | 0.0 | 49.5 |
| Kadlec & Knight | 0.0010 | 3.8 | 0.160 | 0.3 | ||
| Sidiropoulou | 0.0089 | 1.3 | 0.266 | 5.0 |
*L/T Ratio is the ratio between the laminar and turbulent resistance terms
The results indicate a moderate sensitivity to the values of a and b selected for each riprap or rock size. The flow rate through the rubble mound increases with increasing riprap or rock size. For all three formulas, the ratio of the laminar to turbulent resistance force decreases with increasing riprap or rock size, and the ratios tend to be significantly higher for the Siridopoulou (2006) formulation. The percent variation in the simulated flow rate, defined as the maximum difference divided by the average flow rate, increases with increasing riprap or rock size.
The data used to develop the recommended parameter values were typically based on laboratory experiments with rubble mound rock sizes in the range of 1 to 3 cm. The maximum size used in the experiments was 8 cm. Thus for riprap or rock size values that are typical of coastal engineering structures, the values of a and b from formulas of Ward (1964), Kadlec and Knight (1996) and Siridopoulou (2006) represent an extension beyond the rock sizes representing the experimental data base.
Additional Information
Technical details of the rubble mound formulation and numerical implementation are provided in Documentation Portal under Structures Rubble Mounds
References
- Buttolph, A. M., C. W. Reed, N. C. Kraus, N. Ono, M. Larson, B. Camenen, H. Hanson, T. Wamsley, and A. K. Zundel, A. K. 2006. Two-dimensional depth-averaged circulation model CMS-M2D: Version 3.0, Report 2, sediment transport and morphology change. Coastal and Hydraulics Laboratory Technical Report ERDC/CHL-TR-06-7. Vicksburg, MS: U.S. Army Engineer Research and Development Center.
- Forchheim, Ph. "Wasserbevegung durch Boden" , Z. Ver. Deutsh. Ing., Vol. 45, 1901, p.1781-1788
- Kadlec H.R., Knight, L.R., 1996. Treatment Wetlands. Lweis Publishers.
- Melina G. Sidiropoulou Konstadinos N. Moutsopoulos Vassilios A. Tsihrintzis (2007). Determination of Forchheimer equation coefficients a and b. Hydrological Processes, Volume 21, Issue 4, 15, Pages: 534–554.
- Militello, A., Reed, C.W., Zundel, A.K., and Kraus, N.C. 2004. Two-Dimensional Depth-Averaged Circulation Model M2D: Version 2.0, Report 1, Technical Documentation and User’s Guide, ERDC/CHL TR-04-2, U.S. Army Research and Development Center, Coastal and Hydraulics Laboratory, Vicksburg, MS.
- Ward, J.C., 1964. Turbulent flow in porous media. Journal of Hydrualic Division, ASCE 90(5): 1-12