Long-wave Runup: Difference between revisions
No edit summary |
|||
| (9 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
__NOTOC__ | __NOTOC__ | ||
<font color=red>'''UNDER CONSTRUCTION'''</font> | <font color=red>'''UNDER CONSTRUCTION'''</font> | ||
== | == Overview == | ||
The goal of this verification test to asses the model performance in simulating nonlinear runup/rundown over a plane slopt. Carrier et al. (2003) presented an analytical solution to the nonlinear shallow water equations over a plane slope for several initial wave forms. Here the analytical solution for a the initial wave form given by leading-depression N-wave is used. | |||
== Initial Condition == | |||
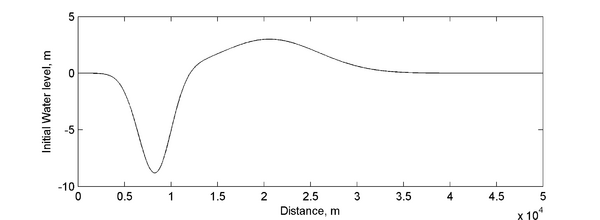
The bed has a constant slope of 1/10 with the initial shoreline located at x=0. Figure 1 shows the initial water level (is given by a leading depression N-wave (characteristic of the waves caused by submarine landslides). The initial current velocity is equal to zero everywhere. | |||
[[Image:Long-wave_Runup_Initial_Water_Level.png|thumb|left|600px| Figure 1. Initial water level]] | |||
<br style="clear:both" /> | |||
== Model Setup == | == Model Setup == | ||
The computational grid has a 3 m resolution for x<300 and increases to 10 m with an aspect ratio of 1.05. The general model parameters used in the simulation are shown in Table 1. | |||
Table 1. Model Parameters | |||
{|border="1" | |||
!'''Parameter''' !! '''Value''' | |||
|- | |||
| Time step || 0.1 s | |||
|- | |||
| Ramp period || 0.0 s | |||
|- | |||
| Drying depth || 0.01 m | |||
|- | |||
| Wall friction || Off | |||
|- | |||
| Mixing terms || Off | |||
|- | |||
| Manning's coefficient || 0.0 | |||
|} | |||
== Results == | == Results == | ||
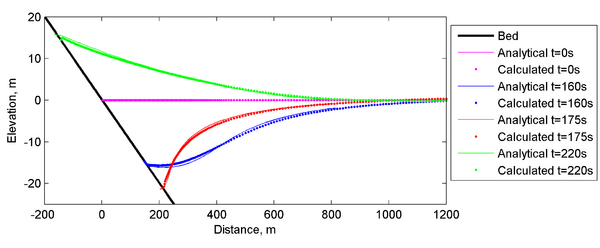
[[Image: | Figure 2 shows a comparison of computed and analytical water surface elevations near the shoreline at 4 different time steps. The goodness of fit statistics are shown in Table 2. | ||
[[Image:Long-wave_Runup_Water_Level.png|thumb|none|600px| Figure 2. Comparison of calculated and analytical water levels for different time steps. ]] | |||
<br style="clear:both" /> | |||
'''Table 2. Goodness of Fit Statistics''' | |||
{| border="1" | |||
! Time, s !! RRMSE, % !! RMAE, % !! R^2 !! Bias, m | |||
|- | |||
| 160 || 3.7 || 3.8 || 0.999 || -0.012 | |||
|- | |||
| 175 || 6.5 || 5.9 || 0.997 || -0.113 | |||
|- | |||
| 220 || 4.6 || 5.4 || 1.000 || -0.066 | |||
|} | |||
* For a definition of the goodness of fit statistics see [[Statistics | Goodness of fit statistics]]. | |||
<br style="clear:both" /> | |||
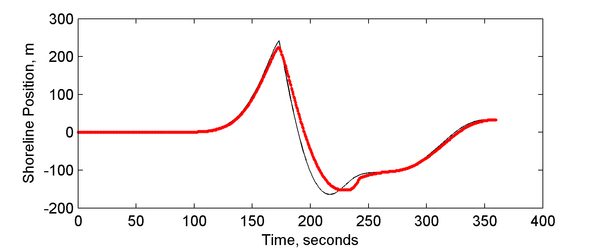
A comparison of the calculated and analytical shoreline position are shown in Figure 3. | |||
[[Image:Long-wave_Shoreline.png|thumb|none|600px| Figure 3. Time series comparison of calculated and analytical shoreline position.]] | |||
<br style="clear:both" /> | <br style="clear:both" /> | ||
== References == | == References == | ||
* Carrier, G., Wu, T.T., and Yeh, H. (2003). "Tsunami runup and draw-down on a plane beach", Journal of Fluid Mechanics, 475, 79-99. | |||
---- | ---- | ||
Latest revision as of 22:06, 11 May 2011
UNDER CONSTRUCTION
Overview
The goal of this verification test to asses the model performance in simulating nonlinear runup/rundown over a plane slopt. Carrier et al. (2003) presented an analytical solution to the nonlinear shallow water equations over a plane slope for several initial wave forms. Here the analytical solution for a the initial wave form given by leading-depression N-wave is used.
Initial Condition
The bed has a constant slope of 1/10 with the initial shoreline located at x=0. Figure 1 shows the initial water level (is given by a leading depression N-wave (characteristic of the waves caused by submarine landslides). The initial current velocity is equal to zero everywhere.
Model Setup
The computational grid has a 3 m resolution for x<300 and increases to 10 m with an aspect ratio of 1.05. The general model parameters used in the simulation are shown in Table 1.
Table 1. Model Parameters
| Parameter | Value |
|---|---|
| Time step | 0.1 s |
| Ramp period | 0.0 s |
| Drying depth | 0.01 m |
| Wall friction | Off |
| Mixing terms | Off |
| Manning's coefficient | 0.0 |
Results
Figure 2 shows a comparison of computed and analytical water surface elevations near the shoreline at 4 different time steps. The goodness of fit statistics are shown in Table 2.
Table 2. Goodness of Fit Statistics
| Time, s | RRMSE, % | RMAE, % | R^2 | Bias, m |
|---|---|---|---|---|
| 160 | 3.7 | 3.8 | 0.999 | -0.012 |
| 175 | 6.5 | 5.9 | 0.997 | -0.113 |
| 220 | 4.6 | 5.4 | 1.000 | -0.066 |
- For a definition of the goodness of fit statistics see Goodness of fit statistics.
A comparison of the calculated and analytical shoreline position are shown in Figure 3.
References
- Carrier, G., Wu, T.T., and Yeh, H. (2003). "Tsunami runup and draw-down on a plane beach", Journal of Fluid Mechanics, 475, 79-99.