CMS-Flow:Hiding and Exposure
Hiding and Exposure
When the bed material is composed of multiple grain sizes, larger grains have a greater probability of being exposed to the flow while smaller parti-cles have a greater probability of being hidden from the flow. Figure 1 shows an example of a sediment grain (dj) being hidden by dk.
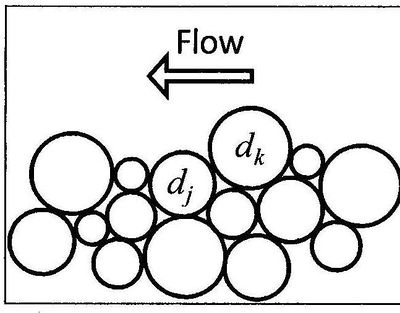
Figure 1. Schematic of the exposure height of bed sediment grains.
For the transport formulas described above, the hiding and exposure mechanism is considered by correcting the critical shear stress or velocity using a hiding and exposure correction function (). For the Lund-CIRP transport formula, an alternate approach is required due to the way in which the Shields number and grain size are included in the formulation; thus, the hiding and exposure correction function is directly used to multiply the transport rate. Two methods are used to calculate depen-ding on whether the sediment transport model is run with a single sediment size or with multiple sediment sizes; the methods are described in the following sections.
Single-Sized Sediment Transport
In some applications, the coastal bed material is dominated by a single sediment size with patches of other sediment sizes or materials (e.g., shell hash) that may not contribute significantly to morphology change in the areas of interest; however, they may modify the sediment transport through hiding and exposure. For example, it is possible for the bed material to consist of mostly uniform sand with patches of shell fragments (bimodal distribution) in some regions. The shell material is difficult to model numerically because it is usually poorly sorted, and its hydraulic properties are unknown. For such regions, sediment transport models often tend to over-estimate erosion since the impacts of hiding effect of the coarser shell material are not represented (e.g., Cayocca 2001). A better and more physically plausible approach is to use the local bed composition along with a correction to account for the hiding and exposure effects of the uniform sand with the patches of coarser shell material. For single-sized sediment transport, the correction function for hiding and exposure is calculated following Parker et al. (1982) as
| (1) |
where m is an empirical coefficient between 0.5 to 1.0. The aforementioned sediment transport equations are implemented by using the transport grain size (dk)rather than the bed material (d50). A single and constant transport size (dk) is used, while the bed material (d50) varies spatially. The spatial distribution of d50 can be obtained from field measurement data and, for simplicity, is assumed constant during the model simulation time. This is a significant assumption and may not be reasonable for some applications. However, this method provides a simple conceptual mechanism for considering an important process in the proposed single-sized sediment transport model. The approach has been successfully applied to Shinnecock Inlet, NY, to simulate morphology change at a coastal inlet (Sánchez and Wu 2011a). A more accurate and complex approach is to simulate the transport and sorting of multiple-sized sediments.
Multiple-Sized Sediment Transport
The hiding and exposure correction for each sediment size class is based on Wu et al. (2000):
| (2) |
where m is an empirical coefficient that varies for each transport formula, approximately equal to 0.6-1.0. The total hiding and exposure probabilities (Pek and Phk, respectively) are calculated as
|
|
(3) |
where N is the number of grain-size classes.
References
- Cayocca, F. 2001. Long-term morphological modeling of a tidal inlet: the Arcachon Basin, France. Coastal Engineering (42):115–142.
- Parker, G., P. C., Kilingeman, and D. G. McLean. 1982. Bed load and size distribution in paved gravel-bed streams. Journal of the Hydraulics Division, ASCE 108(4):544–571.
- Sánchez, A., and W. Wu. 2011a. A non-equilibrium sediment transport model for coastal inlets and navigation channels. Journal of Coastal Research, Special Issue (59):39–48.
- Wu, W., S. S. Y. Wang, and Y. Jia. 2000. Non-uniform sediment transport in alluvial rivers. Journal of Hydraulic Research, IAHR 38(6):427–434.