GenCade Empirical Parameters

Depth of Longshore Transport

The sand bypassing algorithm within GenCade requires a depth of active longshore transport, $D_{LT}$ , which is defined as the depth of breaking of the highest one tenth waves at the updrift side of the structure. Under standard assumptions, this depth is related to the significant wave height $H_{b}$ (meters). This is used throughout as:

$D_{LT}=({\frac {1.27}{\gamma }})H_{b}$

where 1.27 is the conversion factor between the highest one-tenth wave height and the significant wave height, $H_{b}$ is the breaking wave height, and ${\gamma }$ is the breaker index. The depth of longshore transport is typically much less than the depth of closure, except under extreme wave conditions.

The characteristic maximum depth of longshore transport $D_{{LT}_{O}}$ is used to calculate the average beach slope $tan{\beta }$ , which is also used in (Sand Transport Rates). $D_{{LT}_{O}}$ is calculated as introduced in Hallermeier (1983):

$D_{{LT}_{O}}=2.28H_{O}-{\frac {10.9H_{0}^{2}}{L_{O}}}$

where $H_{O}$ is the significant wave height (meters) and $L_{O}$ is the wavelength (meters), both in deep water.

Additionally, the average nearshore slope $tan{\beta }$ is calculated as:

$tan\beta =({\frac {A^{3}}{D_{{LT}_{O}}}})^{\frac {1}{2}}$

In GenCade, $D_{{LT}_{O}}$ is calculated at each time step using the deep water wave data, making the assumption that it is valid across the entire longshore extent of the modeled reach.

Average Profile and Shape

A profile shape must be specified to determine the location of the breaking waves and to calculate the average nearshore bottom slope used in the longshore transport equation. GenCade uses the equilibrium profile shape introduced by Bruun (1954) and Dean (1977):

$D=Ay^{2/3}$

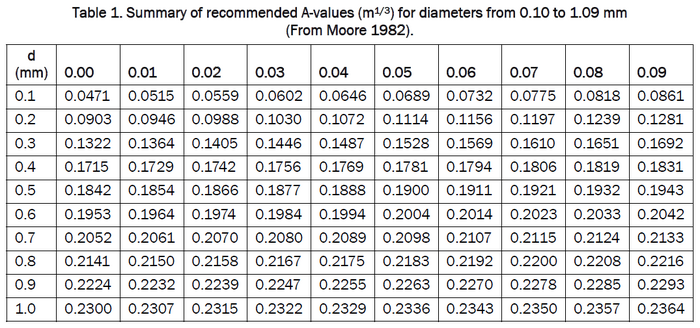
where $D$ is the water depth (meters), $y$ is the distance from the shoreline (meters), and $A$ is the scale parameter (meters^1/3). The scale parameter has been shown (Moore, 1982) to depend on the median grain size ( $d_{50}$ , in millimeters) which in turn effects the settling velocity ( $w_{s}$ , in meters/second). The scale parameter is defined using the Kriebel et al. (1991) relation:

$A=2.25({\frac {w_{s}^{2}}{g}})^{1/3}$

If surveys of the target beach are available, it is recommended that the modeler use the curves in Figure 1 below (1a for metric units or 1b for American customary units) as templates to determine an 'effective' median grain size. The 'effective' grain size, if supplied to GenCade, will produce an A-value that will give the most representative profile shape. If profile survey data are lacking, the median grain size of the surf zone sand should be used. Table 1 is based on the methodology proposed in Moore (1982) and shows a summary of recommended A-values for grain size diameters.

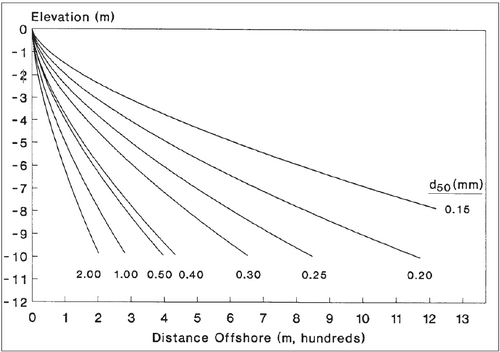
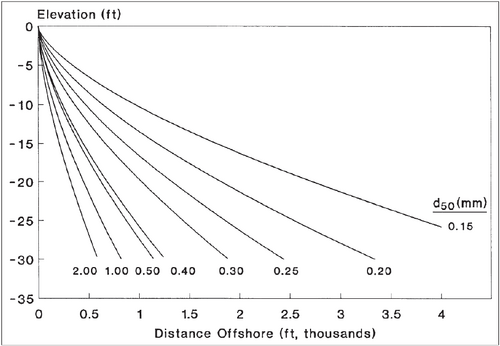
Depth of Closure

The depth of closure, $D_{C}$ , the seaward limit beyond which the profile does not exhibit significant changes in bed elevation, must be specified by the user. Empirically, $D_{C}$ can be difficult to determine, as small bathymetric change in deeper water is difficult to measure. Additionally, survey data are sometimes not available to a sufficient depth and with sufficient vertical and horizontal control to allow comparisons of profiles to obtain estimates of $D_{C}$ . This situation requires the user to apply their judgment and knowledge of the local conditions to specify a representative value. Users are encouraged to contact the GenCade team if they need more guidance when empirical estimates of $D_{C}$ are not available.