CMS-User Guide Part 2: An Overview of CMS-Wave Model Theory, Processes, and Features
CIRP-WN-12-3
Overview
CMS-Wave (Lin et al. 2010; Lin et al. 2008; Demirbilek et al. 2007) is a two-dimensional (2D) spectral wave model formulated from a parabolic approximation equation (Mase et al. 2005) with energy dissipation and diffraction terms. The model, previously called WABED (Wave-Action Balance Equation Diffraction), is part of Coastal Modeling System (CMS) developed in the Coastal Inlets Research Program (CIRP), U.S. Army En-gineer Research and Development Center (ERDC). It simulates a steady-state, spectral transformation of directional random waves co-existing with ambient currents in the coastal zone. The model is designed for accurate and reliable representation of wave processes affecting operation and maintenance of coastal inlet structures in navigation projects as well as in risk and reliability assessment of shipping in inlets and harbors.
CMS-Wave is a phase-averaged model for propagation of directional ir-regular waves over complicated bathymetry and nearshore where wave refraction, diffraction, reflection, shoaling, and breaking simultaneously act at inlets. Additional features such as wind-wave generation, bottom friction, and spatially varied cell sizes have recently been incorporated into the model to make it suitable for more general use in the coastal region. Recent improvements of CMS-Wave include semi-empirical estimates ofwave run-up on beach face and overtopping structures, wave energy damping over muddy bed, and theoretically based nonlinear wave-wave interactions. It can operate on nesting grids, run in a rapid mode, simulate the full plane wave generation, and couple to the circulation, salinity, and sediment transport models in CMS.
Main Features
Wave diffraction terms are included in the governing equations following the method of Mase et al. (2005). Four different depth-limiting wave breaking formulas can be selected as options including the interaction with a current. The wave-current interaction is calculated based on the dispersion relationship including wave blocking by an opposing current (Larson and Kraus 2002). Wave generation and whitecapping dissipation are based on the parameterization source term and calibration using field data (Lin and Lin 2004a and b, 2006a). Bottom friction loss is estimated from the classical drag law formula (Collins 1972).
Other useful features in CMS-Wave include grid nesting capability, variable rectangular cells, wave overtopping, wave runup on beach face, nonlinear wave-wave interactions, and full-plane wave generation. CMS-Wave may be run in a coupled fashion with the CMS-Flow explicit model (Demirbilek and Rosati 2011). This requires using the Steering scheme available in the SMS interface. The Steering essentially is a set of instruction set that determines how wave and flow models will communicate to share calculated results with each other. Two types of communication are possible: one-way or two-way. In the one-way Steering, the wave model provides wave radiation stress gradients to the flow model. These are used to calculate wave-induced currents. Other wave parameters (height, period and direction) are also passed on to the flow model and are used in the flow and sediment transport calculations. However, the flow model does not return any results back to the wave model in the one-way Steering, hence this name. In contrast, in the two-way Steering, the flow model returns to the wave model surface elevation, currents and updated bathymetry (due to sediment transport and bed change) calculated by the flow model. The one-way Steering permits users to include potential effects of waves in the flow model, whereas the two-way Steering provides wave model the water level and bathymetric changes calculated by the flow model. The two-way Steering is appropriate for wave-current interactions. The Steering between the CMS-Wave and CMS-Flow implicit models is not necessary because the wave model is imbedded inside the flow model. This directly coupled system is called the “in-line” model. Consequently, Steering is required only for the CMS-Flow explicit model, but is not needed for the implicit version of CMS-Flow model.
Wave-action Balance Equation with Diffraction
The fundamental theoretical basis of the CMS-Wave is the wave-action balance equation. This equation represents two-dimensional variation of wave energy in space, and takes into account the effect of an ambient horizontal current on wave behavior. This equation may be written as (Mase 2001)
|
|
(1) |
where
|
|
(2) |
is the wave-action density to be solved and is a function of frequency and direction . E(,) is two-dimensional (2-D) spectral wave density representing the wave energy per unit water-surface area per frequency and direction interval. In the presence of an ambient current, the wave-action density is conserved, whereas the spectral wave density is not (Bretherton and Garrett 1968; Whitham 1974). Both wave diffraction and energy dissipation are included in the governing equation.
The numerical solution scheme for solving Equations 1 and 2 is described elsewhere (Mase 2001; Mase et al. 2005). The variables and are wave celerity and group velocity, respectively; x and y are the horizontal coordinates; , , and are the characteristic velocity with respect to x, y, and, respectively; and denote the first and second derivatives of N with respect to y, respectively; is an empirical parameter representing the intensity of diffraction effect; is the parameterization of wave breaking energy dissipation; S denotes additional source and sink (e.g., wind forcing, bottom friction loss, etc.) and nonlinear wave-wave interaction term .
Wave Diffraction
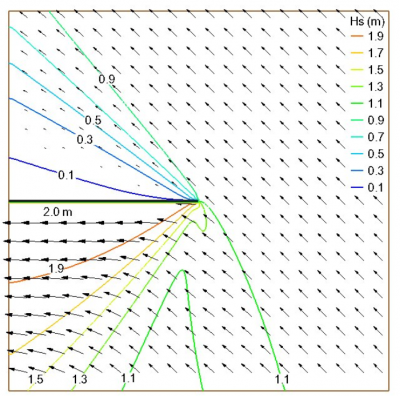
The first term on the right side of Equation (1) is the wave diffraction term formulated from a parabolic approximation wave theory (Mase 2001). In applications, the diffraction intensity parameter needs to be calibrated and optimized for structures. The model omits the diffraction effect for and calculates diffraction for . Large should be avoided as it can cause artificial wave energy losses. In practice, values of between 0 (no diffraction) and 4 (strong diffraction) have been determined in comparison to measurements. A default value of was used by Mase et al. (2001, 2005) to simulate wave diffraction for both narrow and wide gaps between breakwaters. In CMS-Wave, the default value of is 4 corresponding to strong diffraction. This default is recommended for wave diffraction at a semi-inifinite long breakwater or at a narrow gap, with the opening equal or less than one wavelength. For a relatively wider gap, with an opening greater than one wavelength, is recommended. The exact value of in an application is dependent on the structure geometry and adjacent bathymetry, and it may need to be verified with measurements.
Wave-current Interaction
The characteristic velocties , , and in Equation (1) are expressed as:
|
|
(3) |
|
|
(4) |
|
|
(5) |
where U and V are the depth-averaged horizontal current velocity components along the x and y axes, k is wave number, and is water depth. The dispersion relationships between the relative angular frequency , the absolute angular frequency , the wave number vector , and the current velocity vector are (Jonsson 1990)
|
|
(6) |
and
|
|
(7) |
where is the Doppler-shifting term, and g is the gravitational acceleration. The main difference between the wave transformation models with and without ambient currents lies in the solution of the intrinsic frequency. In treatment of the dispersion relation with the Doppler shift, there is no solution corresponding to wave blocking, if intrinsic group velocity is weaker than an opposing current (Smith et al. 1998; Larson and Kraus 2002):
|
|
(8) |
Under the wave blocking condition, waves cannot propagate into a strong opposing current. The wave energy is most likely to dissipate through breaking with a small portion of energy either reflected or transformed to lower frequency components in the wave blocking condition. In CMS-Wave, the wave-action corresponding to the wave blocking is set to zero for the corresponding frequency and direction bin.
Wave Reflection
The wave energy reflected at a beach or upon the surface of a structure is calculated under assumptions that the incident and reflected wave angles are equal and that the reflected energy is a given fraction of the incident wave energy. The reflected wave action Nr is assumed linearly proportional to the incident wave action :
|
|
(9) |
where is a reflection coefficient (0 for no reflection and 1 for full reflection) defined as the ratio of reflected to incident wave height (Dean and Dalrymple 1984).
CMS-Wave calculates the wave energy reflection at a sidewall or a lateral solid boundary within the wave transformation routine. It can also calculate wave reflection off the beach or detached breakwater using a backward marching calculation routine (Mase et al. 2005). Users should be aware that, while the computer run time with the forward reflection can be efficient, the time is almost double for the backward reflection routine.
Wave Breaking Formulas
The simulation of depth-limited wave breaking is essential in nearshore wave models. A simple wave breaking criterion that is commonly used as a first approximation in shallow water, especially in the surf zone, is a linear function of the ratio of wave height to depth. For random waves, the criterion is (Smith et al. 1999)
|
|
(10) |
where Hb denotes the significant breaking wave height. CMS applies a more comprehensive criterion on the limiting steepness by Miche (1951) for random waves as
|
|
(11) |
where is the wave number corresponding to the spectral peak. In the shallow water condition ( small), Equation (11) reduces asymptotically to Equation (10). Iwagaki et al. (1980) verified that Miche’s breaker criterion could replicate laboratory measurements over a sloping beach with a current present provided that the wavelength was calculated with the current included in the dispersion equation.
In CMS-Wave, the depth-limited spectral energy dissipation can be selected from four different formulas: (a) Extended Goda formulation (Sakai et al. 1989), (b) Extended Miche (Battjes 1972), (c) Battjes and Janssen (1978), and (d) Chawla and Kirby (2002). These formulas, considered more accurate for wave breaking on a current, can be divided into two generic categories (Zheng et al. 2008). The first class of formulations attempt to simulate the energy dissipation due to wave breaking by truncating the tail of the Rayleigh distribution of wave height on the basis of some breaker criterion. The Extended Goda and Extended Miche formulas belong to this class. The second category of wave breaking formulas uses a bore model analogy (Battjes and Janssen 1978) to estimate the total energy dissipation. The Battjes and Janssen formula and Chawla and Kirby formula are in this class. The spectral energy dissipation is calculated based on one of these four wave breaking formulas, while the computed wave height is further limited by Equations (10) and (11).
Wind Forcing and Whitecapping Dissipation
The evolution of waves in the large-scale, open coast is more affected by wind-ocean-wave interactions than the nearshore wave-current-bottom processes. The result is a nonlinear wave field that is balanced between wind forcing, whitecapping, and wave growth. The surface wind can feed energy into the existing waves and also generate new waves. On the other hand, the energy can dissipate through whitecapping from turbulence-wave interactions and air-wave-water interactions. In CMS-Wave, these wind forcing and whitecapping processes are modeled as separate sink and source terms.
Wind input source function
The wind-input source Sin is formulated as functions of the ratio of wave celerity C to wind speed W, the ratio of wave group velocity to wind speed, the difference of wind speed and wave celerity, and the difference between wind direction and wave direction (Lin and Lin 2006a):
|
|
(12) |
where
|
|
(13) |
|
|
(14) |
|
|
(15) |
and
|
|
(16) |
is the functional form of the Pierson-Moskowitz (PM) spectrum, is the Phillips constant, and
|
|
(17) |
is a normalized directional spreading. The function F1 presents the wind stress effect, F2 designates Phillips’ mechanisms (Phillips 1957) and F3 accounts the wave age effect. For swell or long waves, the wave group velocity is generally large and F3 < 1. If , then F3 = 0. For short waves, the phase velocity is generally small and F3 > 1.
Whitecapping dissipation function
The wave energy dissipation (sink) (Lin and Lin 2006a) for whitecapping including current and turbulent viscous effect is
|
|
(18) |
with
|
|
(19) |
and
|
|
(20) |
where is a proportionality coefficient, and is for the turbulent viscous dissipation. The wave amplitude is calculated at each grid cell. To avoid numerical instability and considering the physical constraint of energy loss for the dissipation, the function F4 is set to equal to 1 if the computed value is greater than 1.
Wave Generation with Arbitrary Wind Direction
In the case of wind forcing only and with no (zero) wave energy input at the sea boundary, CMS-Wave can assimilate the full-plane wave genera-tion. The model will execute an internal grid rotation based on the given wind direction to calculate the wave field and map the result back to the original grid. This feature is convenient for the local wave generation by wind in a lake, bay, or estuary, neglecting swell from the ocean.
Spatially Varied Spectral Wave Input
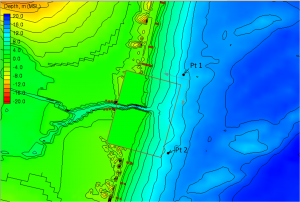
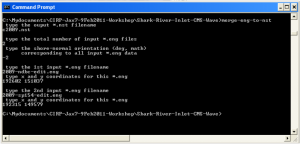
This input will also be used later for the child grid case, where spatially varied wave spectra are assigned to a few user-specified nodes along or near the seaward boundary of the child grid. To apply the spatially varied spectra as wave input without a parent grid, user has to prepare the wave input file with the format as described in the child grid run. A FORTRAN program merge-eng-to-nst.exe (available download from http://cirp.usace.army.mil/wiki/Utilities#Wave_Transformation) is provided to combine all wave spectra files (*.eng) from individual locations into a single wave in-put file in the format for spatially varied spectral input to CMS-Wave. Figure.1 shows the map of two locations that each location has a wave input files available, 2009-ndbc.eng at Pt 1 (coordinates are 192,602 m and 151,037 m) and 2009-sp154.eng at Pt 2 (coordinates are 192,315 m and 149,579 m) – recall that 2009-ndbc.eng and 2009-sp154.eng were originally generated for the parent grid. Figure.2 shows the running of the merge-eng-to-nst.exe in DOS to combine two wave input files into one single wave input file (spatially varied spectral wave input to the child grid). Because 2009-ndbc.eng and 2009-sp154.eng were generated respect to the shore-normal direction at 167 deg and the local child grid orientation is 165 deg, a -2 deg direction adjustment is needed for running the code merge-eng-to-nst.exe here.
It is required that all individual wave input files to cover the same period and timestamps (users must edit the files to fill the missing data). In the example, wave spectra at time stamps 09122000, 0912003, and 0912006 are missing in 2009-ndbc.eng, and wave spectra at timestamps 09120400 and 09121000 are missing in 2009-sp154.eng. Two revised files, 2009-ndbc-edit.eng and 2009-sp154-edit.eng (cover the time period from 09120103 to 09123121 in 3-hr interval) are actually used in merge-eng-to-nst.exe to generate c2009.nst.
Bottom friction loss
The bottom friction loss is calculated by a drag law model (Collins 1972)
|
|
(21) |
with
|
|
(22) |
where presents the ensemble mean of horizontal wave orbital velocity at the sea bed, is the total energy density at a grid cell, and is the Darcy-Weisbach type friction coefficient. The relationship between and the Darcy-Weisbach friction factor is .
Typical values of cf for sandy bottom range from 0.004 to 0.007 based on the JONSWAP experiment and North Sea measurements (Hasselmann et al. 1973; Bouws and Komen 1983). Values of applied for coral reefs range from 0.05 to 0.40 (Hardy 1993; Hearn 1999; Lowe et al. 2005). = 0.005 is the default value in CMS-Wave.
If the Manning friction coefficient is used instead of the Darcy-Weisbach type coefficient, the relationship between the two drag coefficients is (in the SI system)
|
|
(23) |
Estimates of Manning coefficient are available in most fluid mechanics reference books (e.g., 0.01 to 0.05 for smooth to rocky/weedy channels).
Wave Runup
Wave runup is the maximum shoreward wave swash on the beach face for engineering structures such as jetties and breakwaters by wave breaking at the shore. Wave runup is significant for beach erosion as well as wave overtopping of seawalls and jetties. The total wave runup consists of two components: (a) rise of the mean water level by wave breaking at the shore known as the wave setup, and (b) swash of incident waves. In CMS-Wave, the wave setup is computed based on the horizontal momentum equations, neglecting current, surface wind drag and bottom stresses.
|
|
(24) |
|
|
(25) |
where is the water density, are radiation components from the excess momentum flux due to waves. By using the linear wave theory (Dean and Dalrymple 1984), can be expressed as
|
|
(26) |
|
|
(27) |
|
|
(28) |
where . Equations (24) and (25) also calculate the water level depression from the still-water level due to waves known as wave setdown outside the breaker zone. Equation (24) mainly controls wave setup and setdown calculations, whereas Equation (25) predominantly acts to smooth the water level alongshore. The swash oscillation of incident natural waves on the beach face is a random process. The most landward swash excursion corresponds to the maximum wave runup. In the engineering application, a 2% exceedence of all vertical levels, denoted as , from the swash is usually estimated for the wave runup (Komar 1998). This quantity is approximately equal to the local wave setup on the beach or at structures such as seawalls and jetties, or the total wave runup is estimated as
|
|
(29) |
In CMS-Wave, is calculated at the land-water interface and averaged with the local depth to determine if the water can flood the proceeding dry cell. If the wave runup level is higher than the adjacent land cell elevation, CMS-Wave can flood the dry cells and simulate wave overtopping and overwash at them. The feature is useful in coupling CMS-Wave to CMS-Flow (Demirbilek and Rosati 2011; Lin et al. 2011b) for calculating beach erosion or breaching. Calculated quantities of are saved as input to CMS-Flow. CMS-Wave reports the calculated fields of wave setup and maximum water level defined as
| () |
where is referred as the significant wave height.
Use the SMS11.1 interface (Figs.1 and.2) to choose any wave processes to be included in a CMS-Wave simulation. For example, user can select the corresponding options in the SMS to include wave run-up, infra-gravity wave, nonlinear wave-wave interaction, multiple processors, muddy bed, spatial wind field input, and also the binary (xmdf) output option. These wave processes can be included or excluded by user to be considered in simulations. However, user is reminded that additional files are required for the muddy bed and spatial wind field input options.
In applications with a muddy bed in parts or all of modeling domain, user must prepare a mud.dat or *.mud input file in the same format as the *.dep file. This file provides values of the spatial maximum kinematic viscosity for the entire grid. The default value of the kinematic viscosity for mud is zero, and recommended maximum is 0.04 m2/sec.
In applications requiring a spatial wind field input, user should provide a wind.dat or *.wind file in the same format as the *.cur file. This file con-tains the x- and y-component wind speed data that correspond to the incident wave conditions specified by user in the *.eng file.
Wave Transmission and Overtopping at Structures
CMS-Wave applies a simple analytical formula to compute the wave transmission coefficient of a rigidly moored rectangular breakwater of width and draft (Macagno 1953)
| (31) |
Wave transmission over a structure or breakwater is mainly caused by the fall of the overtopping water mass. Therefore, the ratio of the structure crest elevation to the incident wave height is the prime parameter governing the wave transmission. CMS-Wave calculates the rate of overtopping of a vertical breakwater based on the simple expression (Goda 1985) as
| (32) |
where is the crest elevation of the breakwater above the still-water level, and is the incident wave height. Equation (32) is modified for a composite breakwater, protected by a mound of armor units at its front, as
| (33) |
For rubble-mound breakwaters, the calculation of wave transmission is more complicated because the overtopping rate also depends on the spe-cific design of the breakwater (e. g., toe apron protection, front slope, ar-mor unit shape and size, thickness of armor layers). In practice, Equation (33) still can be applied using a finer spatial resolution with the proper bathymetry and adequate bottom friction coefficients to represent the breakwater. For permeable rubble-mound breakwaters, the transmission is calculated from D’Angremond et al. (1996) formula:
| (34) |
where B is the crest width, and is the Iribarren parameter defined as the fore-slope of the breakwater divided by the square-root of deepwater incident wave steepness. In practice, Equations (32) to (34) are applicable to both monochromatic and random waves.
Permeable Structure
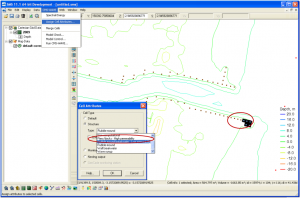
To model a permeable structure in CMS-Wave, it is necessary for user to select and specify which CMS-Wave grid cells cover the permeable struc-ture. This is done in the SMS11.1 interface by using the menu CMS-Wave Assign Cell Attributes and selecting Permeable Breakwater (see Fig.1). In SMS11 or earlier versions which does not have the permeable structure cell feature, users will need to modify the *.struct file manually to specify the permeable structure cells. Each feature cell in the CMS-Wave grid is described by four parameters: istruc, jstruc, kstruc, and cstruc in a line format in the *.struct file. See CMS-Wave Technical Report CHL-TR-08-13 for details. These four parameters and values that user can assign to them are listed below:
- istruc = i-th column in the grid
- jstruc = j-th row in the grid
- kstruc = feature cell id denoting the types of structure
- = 1 (for adding an alternative feature or structure immersed or exposed, without modifying the input depths)
- = 2 (for calculation of wave runup and overwash on beach face or structure and adjacent land)
- = 3 (for calculation of transmitted waves for a floating breakwater)
- = 4 (for a vertical wall breakwater)
- = 5 (for a composite or rubble-mound breakwater)
- = 6 (for a highly permeable structure like the pier or bridge)
- = 7 (for a low-permeable structure, like the rubble-mound breakwater)
- cstruc =feature structure characteristic dimension (could be the
- depth or elevation or draft of structure as defined below)
- = feature structure depth (for kstruc = 1; model assumes a land cell if not provided)
- = beach or structure elevation above mean water level (for kstruc = 2; model uses the input depth if not provided; no effect for cstruc < 0)
- = floating breakwater draft (for kstruc =3; model skips calculations if not provided or cstruc < 0.05 m)
- = breakwater or structure elevation (for kstruc = 4 or 5; model uses the input depth if not provided; immersed if cstruc < 0)
- = the permeable portion (for cstruc >0, but used for the section below the mean water depth of a high-crest structure for kstruc = 6 or 7)
In the example problem provided (Fig.3), user can modify the 2009.struct file to assign the South Jetty 6 seaward end of breakwater cells to be designated with permeable cells. The top 10 lines of the modified 2009.struct are listed below, where the number 191 in the first row is the total structure cells in *.struct file:
191
76 110 7 1.5
77 110 7 1.5
78 110 7 1.5
79 110 7 1.5
76 111 7 1.5
77 111 7 1.5
91 10 5
92 10 5
93 10 5
Grid Nesting
Grid nesting is applied by saving wave spectra at selected locations from a coarse grid (parent grid) and inputting them along the offshore boundary of the smaller fine grid (child grid). For simple and quick applications, a single-location spectrum saved from the parent grid can be used as the wave forcing for the entire sea boundary of the child grid. If multi-location spectra were saved from the parent grid, they are then interpolated as well as extrapolated for more realistic wave forcing along the sea boundary of the child grid.
Multiple grid nesting (e.g., several co-existing child grids and grand-child grids) is supported by CMS-Wave. The parent and child grids can have different orientations, but need to reside in the same horizontal coordinate system. Because CMS-Wave is a half-plane model, the difference between grid orientations between parent and child grids should be small (no greater than 45 deg) for passing sufficient wave energy from the parent to child grids.
Grid nesting allows users to include a sub-grid or “child grid” inside a parent grid. The child grid may be considered in an area where finer grid resolution may be necessary and the parent grid resolution is inadequate. This grid-inside-grid concept allows user to run CMS-Wave only once starting with the parent grid, saving results along the open boundary of the child grid, running the child grid, all in one simulation.
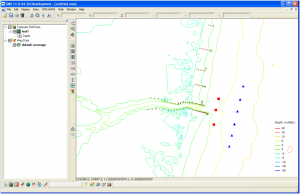
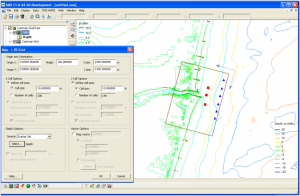
To run the child grid in the Steering mode, the spectral wave input file needs to be renamed to a default “nest.dat” (overwrite the wave input filename in the child *.std). It is noted that this “nest.dat” is only required for the child steering run. The parent grid run must be conducted and completed first to start a child grid run irrespective of whether CMS-Wave is or is not coupled with CMS-Flow (more information in ERDC/CHL CHETN-IV-76).Users can use the CMS-Wave Assign Cell Attributes and Nesting Output (Fig.3) to specify the wave information output cells for saving spectrum data file (to serve as wave input to a child grid run). Figure 4 shows 6 nesting output locations (blue triangle) using the Shark River 2009.sim case. The nesting output file is *.nst (in the case of running CMS steering, an additional file nst.dat is automatically generated that merge all individual cycle *.nst files).
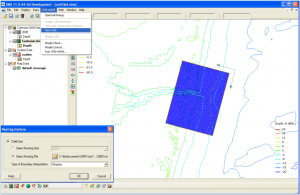
Figure 5 shows a child grid domain (c2009.sim) within the parent grid (the child grid was generated based on scatter points converted from the parent grid). The child grid wave input file (2009.nst, as generated from the parent grid) shall be assigned in the child *.std. This can be done by manually editing the child *.std or using the SMS CMS-Wave and Nest Grid menu (Fig.6).
The child wave input file format is almost identical to the parent *.eng. The only difference is that the child wave input has additional 3 parame-ters (the local x and y coordinates, and local significant wave height at the spectral wave input location) in the individual spectral header along with the regular 5 parameters (spectral id, wind speed, wind direction, spectral peak frequency, water level adjustment) in the parent *.eng. The top 8 lines of 2009.nst is shown below (notice the 5th line is a spectral header for the 1st individual wave input spectrum):
30 35 6 167.00
0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13
0.14 0.15 0.16 0.17 0.18 0.19 0.20 0.21 0.22 0.23
0.24 0.25 0.26 0.27 0.28 0.29 0.30 0.31 0.32 0.33
9120103 9.80 -221.0 0.1200 0.00 192440.33 150712.28 0.563
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
Variable-rectangular-cell Grid
CMS-Wave can run on a grid with variable rectangular cells. This feature is suited to large-domain applications in which wider spacing cells can be specified in the offshore where wave property variation is small and away from the area of interest to save computational time. A limit on the shore-normal to shore-parallel spacing ratio in a cell is not required as long as the calculated shoreward waves are found to be numerically stable.
Non-linear Wave-wave Interaction
The non-linear wave-wave interaction is a conserved energy transfer from higher to lower frequencies. The mechanism can produce transverse waves and energy diffusion in the frequency and direction domains. The effect is more pronounced in the intermediate to shallow water depth. Directional spreading of the wave spectrum tends to increase as the wavelength decreases.
The exact computation of the nonlinear energy transfer involves six-dimensional integrations. This is computationally too taxing in practical engineering nearshore wave transformation models. Mase et al. (2005) have shown that calculated wave fields differ with and without nonlinear energy transfer. CMS-Wave applied a theoretically based formula proposed by Jenkins and Phillips (2001) to calculate the nonlinear wave-wave interaction.
In finite water depth, the nonlinear wave-wave interaction function can be expressed as (Lin et al. 2011a)
| (35) |
where is a function of , , and
| (36) |
Wave Dissipation over Muddy Bed
The calculation the wave dissipation over muddy bed in CMS-Wave is based on the assumption that the turbulent eddy viscosity is several orders of magnitude greater than the kinematic viscosity of sea water. By neglecting the kinematic viscous effect, the wave dissipation over a muddy bed can be expressed as (Lamb, 1932)
|
|
(37) |
where the turbulent eddy viscosity is equal to a maximum viscosity representing the wave breaking condition times the ratio of wave height over depth.
Full-plane and Wind Field Input Capabilities
The full-plane capability of CMS-Wave is ideal for calculating waves in a bay or estuary connected to a major water body. This capability is also essential to simulate storm waves in the open coast or around an island. In the case of strong wind-wave interactions, especially under a hurricane, CMS-Wave can read wind field information, a separate spatial wind field file, for more realistic calculation of wave generation, dissipation, and growth.
In this mode, CMS-Wave performs two half-plane runs in the same grid. The first run is in the half-plane with the principle wave direction toward the shore. The second run is in the seaward half-plane. Upon the completion of the second run, two half-plane results are combined to one full-plane solution. Because the run time for the full-plane is approximately twice of the regular half-plane, users shall consider the full-plane mode only if the full-plane features like wave generation and propagation in a bay or around an island. An example is to run the Shark River wave case, 2009.sim, in the full plane (note the plane-type parameter iview = 1 or 2 in 2009.std for the full plane). Figure 7 shows CMS-Wave Model Control screen in SMS11.1 .
Fast-mode Calculation
CMS-Wave can run in a fast mode for simple and quick applications. The fast mode calculates the half-plane spectral transformation on either five directional bins (each 30-deg angle for a broad-band input spectrum) or seven directional bins (each 5-deg angle for a narrow-band input spectrum or 25-deg angle with wind input) to minimize simulation time. It runs at least five times faster than the normal mode, which operates with 35 directional bins. The fast-mode option is suited for a long or time-pressing simulation if users are seeking preliminary solutions. The wave direction estimated in the fast mode is expected to be less accurate than the standard mode because the directional calculation is based on fewer bins.
Summary
CMS-Wave represents and emphasizes both wave diffraction and wave reflection processes that significantly alter wave transformation at coastal inlets, in particular, those stabilized with jetties. The wave-current interaction is calculated based on the dispersion relationship including wave blocking by an opposing current (Larson and Kraus 2002). Wave generation and whitecapping dissipation are based on the parameterization source term and calibration using field data (Lin and Lin 2004a and b, 2006a). Bottom friction loss is estimated from the classical drag law formula (Collins 1972).
Other useful features in CMS-Wave include grid nesting capability, variable rectangular cells, wave overtopping, wave runup on beach face, nonlinear wave-wave interactions, and full-plane wave generation. CMS-Wave testing, application and validation examples are available from the CIRP Wiki site: http://cirp.usace.army.mil/wiki/Test_Cases and http://cirp.usace.army.mil/pubs/cases .
A CMS-Wave Verification & Validation report, ERDC/CHL-TR-11-10, Re-port 2 (Lin et al. 2011) can be downloaded from the link: http://cirp.usace.army.mil/Downloads/PDF/CHL-TR-11-10-2hi.pdf The complete set CMS-Wave related reports are available from the CIRP website: http://cirp.usace.army.mil/pubs/techreports.html .
Several FORTRAN programs for processing different wind wave source data to supply wind and wave input files to CMS-Wave are available in the link http://cirp.usace.army.mil/wiki/Utilities#Wave_Transformation .
References
- Battjes, J. A. 1972. Set-up due to irregular waves. Proceedings 13th International Conference on Coastal Engineering, ASCE, 1993-2004.
- Battjes, J. A., and J. Janssen. 1978. Energy loss and set-up due to breaking of random waves. Proceedings 16th International Conference Coastal Engineering, ASCE, 569-587.
- Bouws, E., and G. J. Komen. 1983. On the balance between growth and dissipation in extreme, depth limited wind-sea in the southern North Sea. Journal of Physical Oceanography 13:1,653-1,658.
- Bretherton, F. P., and C. J. R. Garrett. 1968. Wave trains in inhomogeneous moving media. Proceedings Royal Society of London A(302):529-554.
- Chawla A., and J. T. Kirby. 2002. Monochromatic and random wave breaking at blocking points. Journal of Geophysical Research 107(C7), 10.1029/2001JC001042.
- Collins, J. I. 1972. Prediction of shallow water spectra. Journal of Geophysical Research 77(15):2693-2707.
- Dean, R. G., and R. A. Dalrymple. 1984. Water wave mechanics for engineers and scientists. Englewood Cliffs, NJ: Prentice-Hall, Inc.
- Demirbilek, Z., L. Lin, and A. Zundel. 2007. WABED model in the SMS: Part 2. Graphical interface. Coastal and Hydraulics Laboratory Engineering Technical Note ERDC/CHL CHETN-I-74. Vicksburg, MS: U.S. Army Engineer Research and Development Center.
- Demirbilek, Z. and J. D. Rosati. 2011. Verification and Validation of the Coastal Modeling System: Report I, Executive Summary. Tech. Report ERDC/CHL-TR-11-10, U.S. Army Engineer Research and Development Center, Coastal and Hydraulics Laboratory, Vicksburg, MS.
- Goda, Y. 1985. Random seas and design of maritime structures. University of Tokyo Press.
- Hardy, T. A. 1993. The attenuation of spectral transformation of wind waves on a coral reef. Queendsland, Australia: James Cook University of North Queensland, Townsville, 336 p.
- Hasselmann, K., T. P. Barnett, E. Bouws, H. Carlson, D. E. Cartwright, K. Enke, J. A. Ewing, H. Gienapp, D. E. Hasselmann, P. Kruseman, A. Meerbrug, P. Muller, D. J. Olbers, K. Richter, W. Sell, and H. Walden. 1973. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Deutsche Hydrographische Zeitschrift A80(12), 95 p.
- Hearn, C. J. 1999. Wave-breaking hydrodynamics within coral reef systems and the effect of changing relative sea level. Journal of Geophysical Research 104(C12):30,007-30,019.
- Iwagaki, Y., T. Asano, Y. Yamanaka, and F. Nagai. 1980. Wave breaking due to currents. Annual Journal of Coastal Engineering 27:30-34, JSCE (in Japanese).
- Jenkins, A. D., and O. M. Phillips. 2001. A simple formula for nonlinear wave-wave interaction. Journal of Offshore and Polar Engineering 11(2):81-86.
- Jonsson, I. G. 1990. Wave-current interactions. Chapter 7, The Sea. B. Le Mehaute and D. Hanes (ed.). New York, NY: John Wiley and Sons, 65-120.
- Komar, P. D. 1998. Beach processes and sedimentation. 2nd ed. Upper Saddle River, NJ: Prentice-Hall, Inc.
- Lamb, H., 1932. Hydrodynamics. 6th ed. New York: Dover Publications.
- Larson, M., and N. C. Kraus. 2002. NMLONG: Numerical model for simulating longshore current. Coastal and Hydraulics Laboratory Technical Report ERDC/CHL TR-02-22. Vicksburg, MS: U.S. Army Engineer Research and Development Center.
- Lin, L., and Z. Demirbilek. 2005. Evaluation of two numerical wave models with inlet physical model. Journal of Waterway, Port, Coastal, and Ocean Engineering 131(4):149-161, ASCE.
- Lin, L., and R.-Q. Lin. 2004a. Wave Breaking Function. Proceedings 8th International Workshop on Wave Hindcasting and Prediction. Oahu, Hawaii: North Shore. November 14-19.
- Lin, R.-Q., and L. Lin. 2004b. Wind Input Function. Proceedings 8th International Workshop on Wave Hindcasting and Prediction. North Shore, Oahu, Hawaii. November 14-19.
- Lin, L., R.-Q. Lin, and J. P.-Y. Maa. 2006a. Numerical simulation of wind wave field. 9th International Workshop on Wave Hindcasting and Prediction. Victoria, British Columbia, Canada, 24-29 September.
- Lin, L., H. Mase, F. Yamada, and Z. Demirbilek. 2006b. Wave-action balance equation diffraction (WABED) model: Tests of wave diffraction and reflection at inlets. Coastal and Hydraulics Engineering Technical Note ERDC/CHL CHETN-III-73. Vicksburg, MS: U.S. Army Engineer Research and Development Center.
- Lin, L., Z. Demirbilek, H. Mase, J. Zheng, and F. Yamada. 2008. CMS-Wave: a nearshore spectral wave processes model for coastal inlets and navigation projects. Tech. Report ERDC/CHL TR-08-13. Vicksburg, MS: U.S. Army Engineer Research and Development Center.
- Lin, L., Z. Demirbilek, and H. Mase. 2011a. Recent capabilities of CMS-Wave: A coastal wave model for inlets and navigation projects. Journal of Coastal Research, Special Issue 59, 7-14.
- Lin, L., Z. Demirbilek, R. Thomas, and J. Rosati III, 2011b. Verification and Validation of the Coastal Modeling System, Report 2: CMS-Wave, ERDC/CHL-TR-11-10, US Army Engineer Research and Development Center, Coastal and Hydraulics Laboratory, Vicksburg, Mississippi.
- Lowe, R. J., J. L. Falter, M. D. Bandet, G. Pawlak, M. J. Atkinson, S. G. Monismith, J. R. Koseff. 2005. Spectal wave dissipation over a barrier reef. Journal of Geophysical Research 110(C04001), doi:10.1029/2004JC002711, 16 p.
- Macagno, E. O. 1953. Houle dans un can presentent un passage en charge. La Houille Blanche 9(1):10–37.
- Mase, H. 2001. Multidirectional random wave transformation model based on energy balance equation. Coastal Engineering Journal 43(4):317-337 JSCE.
- Mase, H., K. Oki, T. S. Hedges, and H. J. Li. 2005. Extended energy-balance-equation wave model for multidirectional random wave transformation. Ocean Engineering 32(8-9):961-985.
- Miche, M. 1951. Le pouvoir reflechissant des ouvrages maritimes exposes a 1’action de la houle. Annals des Ponts et Chau.ssess. 121e Annee: 285-319 (translated by Lincoln and Chevron, University of California, Berkeley, Wave Research Laboratory, Series 3, Issue 363, June 1954).
- Phillips, O. M. 1957. On the generation of waves by turbulent wind. Journal of Fluid Mechanics 2:417-445.
- Sakai, S., N. Kobayashi, and K. Koike. 1989. Wave breaking criterion with opposing current on sloping bottom: an extension of Goda’s breaker index. Annual Journal of Coastal Engineering 36:56-59, JSCE (in Japanese).
- Smith, J. M., D. T. Resio, and A. Zundel. 1999. STWAVE: Steady-state spectral wave model, Report 1: User’s manual for STWAVE Version 2.0. Coastal and Hydraulics Laboratory Instruction Report CHL-99-1. Vicksburg, MS: U.S. Army Engineer Waterways Experiment Station.
- Smith, J. M., W. C. Seabergh, G. S. Harkins, and M. J. Briggs. 1998. Wave breaking on a current at an idealized inlet. Coastal and Hydraulics Laboratory Technical Report CHL-98-31. Vicksburg, MS: U.S. Army Engineer Waterways Experiment Station.
- Whitham, G. B. 1974. Linear and nonlinear waves. New York, NY: John Wiley.
- Zheng, J., H. Mase, Z. Demirbilek, and L. Lin. 2008. Implementation and evaluation of alternative wave breaking formulas in a coastal spectral wave model. Ocean Engineering
Appendix A: Description of Input Files
ASCII CMS-Wave Spectral File (*.eng)
Users can use SMS10.1 or higher versions, or use FORTRAN codes outside SMS ( http://cirp.usace.army.mil/wiki/Utilities#Wave_Transformation), to generate the spectral file (*.eng) as input for CMS-Wave.
A portion of a sample energy file is shown below:
30 35
0.040 0.050 0.060 0.070 0.080 0.090 0.100 0.110 0.120 0.130 0.140 0.150 0.160 0.170 0.180 0.190 0.200 0.210 0.220 0.230 0.240 0.250 0.260 0.270 0.280 0.290 0.300 0.310 0.320 0.330
08010100 5.00 10.00 0.130 0.500
0.00000 0.00000 0.00000 0.00000 0.00000 0.00000
0.00000 0.00000 0.00000 0.00000 0.00000 0.00000
0.00000 0.00000 0.00000 0.02000 0.13000 0.25000
...
The first line defines the dimension of the spectral grid (number of fre-quency bins and number of direction bins in a half plane). The next several lines define the frequency values for the grid. Following the grid specification, the file includes a definition line for each directional spectrum consisting of an identifier (08010100 in the example), wind speed (m/sec) and wind direction (deg) for this spectrum (5 m/sec and 10 deg in this sample case), a spectral peak frequency (0.13 Hz in the example), a tidal offset (0.5 m above the model mean water level), and then an energy density (m2 sec/radian) for each cell in the spectral grid (listed by free format in double loops with inner loop for direction bins and outer loop for frequency bins).
ASCII CMS-Wave Depth File (*.dep)
The CMS-Wave depth file is automatically generated when the CMS-Wave simulation file (*.sim) is saved under SMS10.1 or higher versions.
A sample depth file is shown below:
3 6 100.00 200.00
9.93125 9.79375 9.65625 7.51875 3.38125 1.24375
8.55625 7.41875 5.28125 3.14375 1.00625 -0.86875
8.18125 7.04375 4.90625 2.76875 -0.63125 -1.49375
The first line contains the number of rows (=3), columns and (=6) the size of cells in the x and y directions (100 and 200 m in the example). Depth values are then specified for each cell in the row-to-row order (from top row to bottom row in the model domain).
CMS-Wave Model Parameters File (*.std)
Users can use SMS11 or higher versions, or simply edit the existing model control file *.std, to specify/select these advanced features. The *.std file has 25 input parameters. The first 15 parameters are the basic parameters as described in the CMS-Wave Technical Report (CHL-TR-08-13). The remaining 10 parameters are relatively new for advanced CMS-Wave features described in a recently published model Verification & Validation report, ERDC/CHL-TR-11-10, Report 2 (Lin et al. 2011). These input parameters are listed below and description of each parameter is provided in Table 1:
| 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | 9th | 10th | 11th | 12th | 13th | 14th |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| iprp | icur | ibk | irs | kout | ibnd | iwet | ibf | iark | iarkr | akap | bf | ark | arkr |
| 15th | 16th | 17th | 18th | 19th | 20th | 21st | 22nd | 23rd | 24th | 25th |
|---|---|---|---|---|---|---|---|---|---|---|
| iwvbk | nonln | igrav | irunup | imud | iwnd | isolv | ixmdf | iproc | iview | iroll |
Among these 25 parameters in the *.std file, the first 6 parameters are always required in CMS-Wave and the remaining ones starting any parameter after the 6th will be assigned to the default values if not provided in the *.std. The more specific use and options associated with each of these 1st to 25th parameters are given in Table A.1
Table A.1 Description of CMS-Wave input parameters in the *.std file
| Number | Variable | Argument Type |
Options/Range | Description |
|---|---|---|---|---|
| 1 | iprp | integer | 0 - waves and wind input in *.eng 1 - waves only, neglect wind input in *.eng |
Wave propagation mode. |
| 2 | icur | integer | 0 - no current input 1 - with current input *.cur |
Current interaction. |
| 3 | ibk | integer | 0 - no wave breaking output 1 - output breaking indices |
Wave breaking output option. |
| 4 | irs | integer | 0 - no wave radiation stress calculation or output 1 - calculate and output radiation stresses |
Radiation stress and runup options. |
| 5 | kout | integer | >= 0 | Number of special wave output location, output spectrum in *.obs and parameters in selhts.out. |
| 6 | ibnd | integer | 0 - no input a parent spectrum *.nst 1 - read *.nst, averaging input spectrum |
Nesting option. |
| 7 | iwet | integer | 0 - allow wet/dry, default 1 - without wet/dry |
Wetting and drying options. |
| 8 | ibf | integer | 0 - no bottom friction calc 1 - constant Darcy-Weisbach coef, c_f |
Bottom friction option. |
| 9 | iark | integer | 0 - without forward reflection 1 - with forward reflection |
Forward reflection option. |
| 10 | iarkr | integer | 0 - without backward reflection, 1 - with backward reflection |
Backward reflection option. |
| 11 | akap | real | 0.0<=akap<=4.0 | Diffraction intensity coefficient. |
| 12 | bf | real | >=0 | constant bottom friction coef cf or n (typical value is 0.005 for cf and 0.025 for Mannings n). |
| 13 | ark | real | 0.0<=ark<=1.0 | Constant forward reflection coef, global specification (0 for zero reflection, 1 for full reflection). |
| 14 | arkr | real | 0.0<=arkr<=1.0 | Constant backward reflection coef, global specification (0 for zero reflection, 1 for full reflection). |
| 15 | iwvbk | integer | 0 - Goda-extended 1 - Miche-extended |
Option for the primary wave breaking formula. |
| 16 | nonln | integer | 0 - none, default 1 - nonlinear wave-wave interaction |
Nonlinear wave-wave interaction. |
| 17 | igrav | integer | 0 - none, default 1 - infra-gravity wave enter inlets |
Infragravity waves option. |
| 18 | irunup | integer | 0 - none, default 1 - automatic, runup relative to absolute datum |
Runup option. |
| 19 | imud | integer | 0 - none default 1 - Mud dissipation on |
Mud dissipation option. The kinematic viscosity is specified in mud.dat in units of m2/sec. |
| 20 | iwnd | integer | 0 - none, default 1 - Spatially variable wind on |
Spatially variable wind field option. The winds are specified in wind.dat in units of m/s and in the reference frame of the CMS-Wave grid. |
| 21 | isolv | integer | 0 - GSR solver, default 1 - ADI |
Matrix solver for CMS-Wave. |
| 22 | ixmdf | integer | 0 - output ascii, default 1 - output xmdf |
XMDF input and output options. |
| 23 | iproc | integer | >=0 | Number of threads for parallel computing. Optimum number is approximately equal to the total row number divided by 300. Only for isolv = 0. |
| 24 | iview | integer | 0 - half-plane, default 1 - full-plane (Bay and Inlet) |
Half-plane/full-plane option. Users can provide additional input wave spectrum file wave.spc (same format as the *.eng) along the opposite side boundary an imaginary origin for wave.spc at the opposite corner; users can rotate the CMS-Wave grid by 180 deg in SMS to generate this wave.spc. |
| 25 | iroll | integer | = 0 for no effect (default) = 4 for strongest effect. |
Wave roller effect. Incorporation of the roller effect is recommended with finer grid resolution in the surf zone, say, with cross-shore spacing < 10 m |
Appendix B: Buoy Data Input to CMS-Wave
Directional spectral data collected by NDBC or CDIP buoys can be pro-cessed as alternative source for wave input to CMS-Wave. Two examples are given below using CDIP 154 and NDBC 44025 standard spectral files for December 2009. For NDBC buoy data: run ndbc-spectra.exe (FORTRAN, can be down-loaded from http://cirp.usace.army.mil/wiki/Utilities#Wave_Transformation) to read the NDBC standard directional wave file and generate the CMS-Wave input spectral *.eng file by following these steps:
- Download the NDBC standard monthly directional wave spectral file from http://www.nodc.noaa.gov/BUOY/buoy.html (e.g., 44025_200912) - see Figs B.1 to B.4 for accessing NDBC spectral data from the Web.
- In the DOS window, run ndbc-spectra.exe
- Responding to the on-screen input, type the NDBC spectral filename
- Type the starting timestamp (default value is 0) for saving output files
- Type ending timestamp (default is 99999999) for saving output files
- Type the time interval (hr) for saving output data
- Type 2 to save the CMS-Wave *.eng and *.txt files
- Type the CMS-Wave input spectrum filename (*.eng)
- Type the local shoreline orientation (the CMS-Wave grid y axis) in clockwise polar coordinates (deg, positive from North covering the sea, e.g., 180 deg for St Mary’s Entrance, FL/GA, or 360 deg - the wave grid orientation angle in *.sim)
- Type the NDBC buoy location water depth (m) and then the CMS-Wave seaward boundary mean water depth (m), e.g. Buoy 44025 has a nominal depth of 36.3 m relative to Mean Sea Level
- Type 1 to include wind or 0 to skip the wind input infor-mation
- Type 1 or 2 or 3 for different choice of calculated frequency bins to complete the run – see Fig B.5 for running ndbc-spectra.exe in DOS.
- The output files include *.txt, *.eng, *.out (time series of wave parameters at the buoy), and *.dat (time series of shoreward wave parameters at the CMS-Wave offshore boundary).
-
Figure B.1 NODC buoy data access website.
-
Figure B.2 NODC buoy data access world map.
-
Figure B.3 NODC buoy data access regional map.
-
Figure B.4 NDBC buoy spectral data download website.
-
Figure B.5 Run ndbc-spectra.exe in DOS.
For CDIP buoy data: run cdip-spectra.exe (FORTRAN code, available from http://cirp.usace.army.mil/wiki/Utilities#Wave_Transformation) to read the CDIP standard directional wave file and generate the CMS-Wave input *.eng file. Download the CDIP wave file from this website: http://cdip.ucsd.edu/?nav=historic&sub=data (e.g., sp154-200912). See Figs B.6 to B.8.
Run cdip-spectra.exe in the DOS window similar to ndbc-spectra.exe – see Fig B.9. Because CDIP spectral file already contains the buoy location depth information, cdip-spectra.exe will not prompt for this depth input. For processing either NDBC or CDIP data, users shall check and manually fill any data gaps in *.eng and *.txt files (using the first available spectral data from the neighboring time interval).
-
Figure B.6 CDIP buoy data access website.
-
Figure B.7 CDIP buoy data access website.
-
Figure B.8 CDIP buoy data spectral data download website.
-
Figure B.9 Run cdip-spectra.exe in DOS.