GenCade:Boundary Conditions

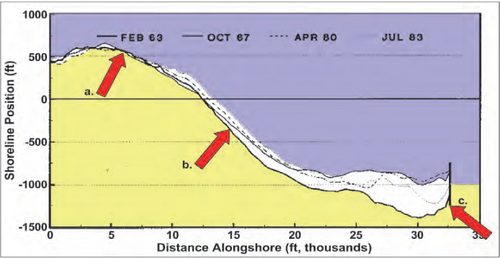
GenCade presently has three options for boundary conditions: pinned, moving, and gated. A boundary condition specified as pinned means that the boundary will not move from the initial shoreline position over the calculation interval. This is the default boundary condition. If a moving boundary condition is selected, the boundary will move a specified distance over a certain time period (specified by the user). The pinned and moving beach boundary conditions should be located far away from the project to assure that the conditions in the vicinity of the boundary are unaffected by changes that take place in the project. A gated boundary condition is bounded with a groin. Figure 1 shows plotted shorelines at Anaheim Beach, CA, where location (a) displays a pinned beach behavior (because all shorelines fall on top of each other here), location (b) represents the moving beach boundary because of the constant rate of accretion (noticed because there is a near-equal distance between consecutive shorelines) and location (c) could be specified as a gated beach (because of the presence of a groin/jetty).

Figure 1. Measured shorelines at Anaheim Beach, CA, where arrows indicate possible boundary condition positions. (A) Pinned beach, all shorelines fall on top of each other at this point (B) Beach moving at a constant rate, near equal distance between consecutive shorelines (C) Gated Beach, presence of groin/jetty

Pinned Beach

It is helpful to draw all available measured shoreline position surveys on the same plot to determine locations along a beach that might be used as model boundaries. In doing so, it is sometimes possible to find a portion of the beach distant from the project that does not move appreciably in time, as shown in Figure 6 for a sandy beach or for regions with a hardened shoreline. By locating the model boundary at such a section, the modeled lateral boundary shoreline coordinate can be said to be ‘pinned’. Expressed in terms of the transport rate, this means:

$Q_{1}=Q_{2}$ or $Q_{N+1}=Q_{N}$

depending on which end of the calculation grid is considered. These relations can be readily understood by reference to the original governing equation (see Governing Equations); if the Q differential with respect to x is zero at the boundary, then the y differential with respect to t is also zero, meaning y does not change over time.

Moving Beach

If a section of beach cannot be found to be represented by the pinned beach boundary condition, it might be possible to locate a section where the shoreline is moving with a constant rate of change $y_{RC}$. In such a case, the boundary condition can be expressed as:

$y_{n}^{t+1}=y_{N}^{t}+y_{RC}$

where the superscripts denote the relative time. In GenCade, the boundary condition is expressed in terms of transport rates. Again, with reference to the initial governing equation, the boundary condition may be formulated as:

$Q_{N}^{t}+1=Q_{N}^{t}-{\frac {y_{RC}-(D_{B}+D_{C})q_{N}^{t}}{2B}}$

where $B={\frac {\delta t}{(2(D_{B}+D_{C})\delta x)}}$ and q is a line source/sink.